Material impresso

PCNA-FÍSICA ELEMENTAR
NOÇÕES DE CÁLCULO
DIFERENCIAL E INTEGRAL NA
CINEMÁTICA.
Tópicos:
5.1 - Objetivos do Capítulo;
5.2 – Uma breve discussão sobre Referencial do
ponto de vista da Cinemática;
5.3 – Posição x Deslocamento;
5.4 - Velocidade média x Velocidade escalar
média;
5.5 – Velocidade instantânea;
5.6 – Noções de cálculo diferencial;
5.7 - Aceleração média x Aceleração escalar
média;
5.8 – Aceleração instantânea;
5.9 – Noções de cálculo integral;
5.10 – Aplicações na cinemática;
5.1 OBJETIVOS DO CAPÍTULO:
 Entender como ocorre o estudo do movimento
via introdução dos conceitos básicos da
cinemática. São eles: posição, deslocamento,
velocidade e aceleração.
 Compreender os fundamentos (aspectos
essenciais) do cálculo diferencial e integral
aplicados em problemas da cinemática.
 Mostrar exemplos de aplicações de cálculo
diferencial nas engenharias em nível
informativo introdutório.
INTRODUÇÃO
O cálculo diferencial e integral é um ramo da
matemática muito adequado para tratar questões
dinâmicas de uma maneira geral. Determinar
como determinadas quantidades variam ou
determinar a quantidade total (valores) de uma
grandeza num dado intervalo (de qualquer
natureza) são problemas gerais que podem ser
atacados por essa área da matemática. Hoje em
dia, o cálculo é usado para achar órbitas de
satélites, estimar o crescimento populacional,
calcular a inflação, e também é utilizado em
questões
importantes
de
processos
de
otimização. Assim, o cálculo diferencial e integral
é hoje considerado um instrumento indispensável
em todos os campos da ciência pura e aplicada:
em Física, Química, Biologia, Astronomia e
principalmente em todas as Engenharias. Isso
nos mostra que as aplicações de cálculo estão
entre as maiores realizações intelectuais da
civilização, tanto do ponto de vista científico,
como também do ponto de vista cultural e social.
E você, prezado leitor, terá oportunidade de ter
um primeiro contato com esse maravilhoso e
vasto campo do conhecimento humano tendo a
cinemática como porta de entrada (aqui neste
capítulo nos restringiremos ao movimento em
linha reta, ou seja, restritos a uma dimensão).
Isso mesmo, o estudo do movimento é um dos
muitos campos da física em que o cálculo
diferencial e integral é importante3.
A ideia é colocar aqui os elementos fundamentais
mais básicos do cálculo diferencial e integral. Em
síntese, queremos lhe dar uma primeira visão do
assunto a partir de três frentes:
 Dando uma ideia geral do que é tratado nessa
área da matemática;
 Apresentando características básicas do
cálculo em nível conceitual-operacional, mas
sem aprofundar no rigor matemático;
 Relacionando
a
estrutura
conceitualoperacional do cálculo com as representações
gráficas correspondentes.
Além disso, para que essa introdução seja
valiosa e representativa para você é necessário o
entendimento das relações entre os conceitos
cinemáticos tanto do ponto de vista conceitualoperacional quanto do ponto de vista gráfico.
Isso quer dizer que precisaremos ter domínio das
ferramentas do cálculo (em nível básico) e
entendimento dos conceitos da cinemática
conforme acabamos de mencionar. Mas temos
mais uma coisa para dizer para você, leitor. Não
apenas isso é possível de ser conseguido como
também tem tudo para ser muito divertido!
3
O físico inglês Isaac Newton estudava questões
relacionadas ao movimento e às explicações do
movimento
(dinâmica).
Pelas
necessidades
matemáticas implicadas em tais estudos, com muita
labuta e genialidade, desenvolveu o início do que
conhecemos hoje como cálculo diferencial e integral.
Outro inventor do cálculo foi o filósofo, e matemático
alemão Gottfried Wilhelm Leibniz. Ambos os gênios,
dos maiores que a humanidade já conheceu, se
envolveram em uma terrível pendenga pela honra de
ter a primazia na invenção do cálculo. Tal briga
polarizou boa parte dos cientistas europeus daquela
época, com os ingleses, ficando do lado de Newton
enquanto que os cientistas alemães tomaram partido
por Leibniz.
49
PCNA-FÍSICA ELEMENTAR
5.2 UMA BREVE DISCUSSÃO SOBRE
REFERENCIAL DO PONTO DE VISTA DA
CINEMÁTICA
Antes de comentarmos sobre os aspectos de
posição e deslocamento é importante nos basear
no que o referencial pode interferir diretamente
nestas duas grandezas físicas posição e
deslocamento. Por exemplo, numa conversa por
telefone ao dizer a sua posição a alguém você
fatalmente adotará um referencial que também
seja conhecido para a pessoa com quem você está
falando (Exemplo: Tô aqui perto do Mercado de
São Braz!).
Mas afinal de contas o que é referencial?
Já discutimos um pouco sobre referencial no
capítulo de vetores quando tratamos da adoção de
um sistema de eixos coordenados para fazer a
decomposição de vetores (ver seção 2.5). Também
falamos de referencial no início do capítulo de Leis
de Newton quando vimos que referenciais que
estão acelerados (referenciais não-inerciais) se
comportam e são descritos de maneira diferente
dos referenciais que não estão acelerados
(referenciais inerciais) (seção 4.2).
Vamos falar mais um pouco sobre referencial,
agora no contexto de cinemática. Conforme
expresso no início desta introdução, a nossa
discussão está restrita a movimentos em uma
dimensão. Ou seja, tudo acontece em cima de uma
linha reta. Essa discussão pode ser facilmente
generalizada para duas e três dimensões, pois nós
temos conhecimento de vetores!
Mas voltemos à discussão. Toda medida de
posição se faz a partir de um ponto. Fisicamente
esse ponto é a nossa origem (onde a gente põe o
“zero”
da
fita
métrica,
por
exemplo).
Matematicamente, é a origem do nosso sistema de
eixos coordenados (lá na seção 2.5 nós já
havíamos falado sobre a necessidade de adotar
formalmente um sistema de coordenadas para
efetuar medidas de posição).
Todo eixo
coordenado possui uma parte positiva a partir da
origem e uma parte negativa a partir da mesma.
Veja a Figura 5.1.
Figura 5.1 Indicação de Referencial graduada em
metros.
Digamos que um objeto esteja na posição 1m
(portanto, à direita da origem). Se o objeto estiver a
mesma da distância da origem, mas à esquerda
desta, ele estará na posição -1m.
Essa discussão é importante para o conceito
deslocamento (que também já foi mencionado no
capítulo de vetores). Como já foi dito,
deslocamento é um conceito vetorial. No exemplo
que estamos desenvolvendo, embora a distância
para a origem seja a mesma (nos casos +1m ou 1m) faz diferença do ponto de vista de
deslocamento se o objeto sai da origem para a
posição +1m ou da origem para a posição -1m. Ou
seja, para o deslocamento não importa apenas o
quanto ele anda, mas também para onde ele anda
(direção e sentido). Veremos esses aspectos com
mais detalhes na seção seguinte.
Não vamos desenvolver extensivamente o estudo
da cinemática. Nosso interesse é abordar tudo o
que é estritamente necessário para o estudo da
dinâmica. Logo, não vamos desenvolver aqui
estudos e manipulações de equações cinemáticas.
Mas fica o alerta! Quando for tratar problemas de
cinemática, não tente apenas decorar as equações
e usa-las cegamente. Estabeleça o seu
referencial, ou seja, estabeleça a origem do seu
sistema de medidas e oriente o sistema de
eixos coordenados que você estiver trabalhando.
Esse é o primeiro passo. Sempre! Depois veja
como essa escolha afeta as equações que você
está trabalhando. Caso resolva “pular” essa etapa,
com alta probabilidade você encontrará o resultado
errado para o problema que está resolvendo ou de
fato não será capaz de explicar como o resolveu,
mesmo que esteja “certo” (a última parte tem
probabilidade igual a 100%).
50
PCNA-FÍSICA ELEMENTAR
5.3 POSIÇÃO X DESLOCAMENTO
IMPORTANTE!
Para estabelecer um referencial do ponto
de vista da cinemática, precisamos
estabelecer a origem do seu sistema de
coordenadas, bem como a orientação do
sistema de eixos coordenados.
IMPORTANTE!
É importante reconhecer a diferença entre
deslocamento e distância percorrida. A
distância percorrida por uma partícula é o
comprimento do caminho descrito pela
partícula de sua posição inicial até a sua
posição final. Deslocamento é a variação de
posição de uma partícula.
O que é posição?
Posição, de maneira simples, é a localização de
um corpo ou objeto em um determinado espaço
em relação a um referencial estabelecido por quem
está efetuando a análise. Ou seja, para medir a
posição de alguém, precisamos medi-la a partir de
um ponto (origem do referencial).
Para descrever o movimento de uma partícula,
precisamos ser capazes de descrever a posição
da partícula e como essa posição varia enquanto
essa partícula se move para um ponto final. Para o
movimento unidimensional, normalmente fazemos
é escolhermos o eixo x como linha ao longo da
qual o movimento o movimento ocorre, mas pode
ser o eixo y como, por exemplo, queda livre.
O que é deslocamento?
Em relação ao deslocamento já vimos que é uma
grandeza vetorial. Um aspecto crucial para efeito
de deslocamento é que importa apenas as
posições: final e inicial que o corpo ocupa. Ou seja,
para efeito de deslocamento não importa o
caminho tomado para ir do ponto inicial ao ponto
final. Duas pessoas que saem do mesmo ponto de
partida e chegam a um mesmo local possuem o
mesmo deslocamento, independente do espaço
que percorrem para fazer esse trajeto.
A propósito! A origem do verbo deslocar significa
tirar de uma localização e levar para outra
localização. Tão somente isso! Com base no que
foi discutido acima, responda: Um corpo sai de
uma determinada posição, dá “meia volta ao
mundo” e volta para a mesma posição. Esse corpo
teve um deslocamento nulo ou diferente de zero?
O deslocamento é a diferença entre as posições
̅e𝒙
̅𝒐 ).
final e inicial (𝒙
⃗ =𝒙
⃗ -𝒙
⃗ 𝒐 (5.1)
∆𝒙
Onde temos como variáveis:
⃗ – Deslocamento.
∆𝒙
⃗𝒙 – Posição Final.
⃗ 𝒐 – Posição Inicial.
𝒙
5.4 VELOCIDADE MÉDIA
ESCALAR MÉDIA
X
VELOCIDADE
Qual a diferença entre essas velocidades?
A diferença é que a velocidade média é uma
grandeza vetorial e a velocidade escalar média é
uma grandeza escalar. Podemos perceber essa
afirmação na própria definição de ambas como se
segue abaixo:
Velocidade Vetorial Média
A velocidade vetorial média é a razão entre o
vetor deslocamento e o tempo transcorrido (∆t).
⃗ =
𝒗
⃗ −𝒙
⃗𝒐
𝒙
𝒕− 𝒕𝒐
=
⃗
∆𝒙
∆𝒕
(5.2)
⃗ é a posição final no instante
Onde: 𝒙
⃗𝒐
𝒕 final e 𝒙
é a posição inicial no instante 𝒕𝒐 inicial.
51
PCNA-FÍSICA ELEMENTAR
IMPORTANTE!
O vetor velocidade média é um vetor que
aponta na mesma direção e no mesmo
sentido que o deslocamento, pois a
constante ∆𝒕 é sempre positiva. Do mesmo
modo que no deslocamento, usaremos os
sinais de mais (+) e o de menos (-) para
indicar os dois sentidos possíveis para
uma dada direção.
Velocidade Escalar Média
A velocidade escalar média é a razão entre a
posição percorrida e o tempo gasto para realizar
o percurso.
𝒗𝒆𝒔𝒄𝒂𝒍𝒂𝒓 =
𝑷𝒐𝒔𝒊çã𝒐 𝑷𝒆𝒓𝒄𝒐𝒓𝒓𝒊𝒅𝒂
𝑻𝒆𝒎𝒑𝒐 𝑮𝒂𝒔𝒕𝒐
(5.3)
Obs.: Unidade no SI: metros por segundo (m/s).
5.5 VELOCIDADE INSTANTÂNEA
Antes de analisarmos o conceito de velocidade
instantânea vamos ver o exemplo abaixo para
esclarecer com mais detalhes o significado de
velocidade instantânea.
Em uma competição de Moto Cross, um
engenheiro, por meio de equipamentos de
medição, conseguiu descrever a função posição
de uma das motos como apresentado a seguir:
𝒙(𝒕) = 𝟓𝒕𝟐
Calcule a velocidade média nos instantes t = 1s e
t = 2s.
𝑥(2) − 𝑥(1)
20 − 5
𝑚
𝑣=
=
= 15 ; 𝛥𝑡 = 1𝑠
𝑡1 − 𝑡0
2− 1
𝑠
𝑥(1,1) − 𝑥(1)
20 − 5
𝑚
𝑣=
=
= 10,5
; 𝛥𝑡 = 0,1𝑠
𝑡1 − 𝑡0
1,1 − 1
𝑠
𝑥(1,01) − 𝑥(1)
20 − 5
𝑚
𝑣=
=
= 10,05 ; 𝛥𝑡 = 0,01𝑠
𝑡1 − 𝑡0
1,01 − 1
𝑠
IMPORTANTE!
À medida que ∆𝐭 diminui, a velocidade
média se aproxima de um valor-limite, que
é a velocidade instantânea. Para poder
entender melhor a definição de velocidade
instantânea, precisamos aprimorar o
entendimento do que vem a ser calculo
diferencial e integral.
5.6 NOÇÕES DE CÁLCULO DIFERENCIAL
Para começar, qual o problema fundamental que
o cálculo diferencial responde? Procuraremos
responder intuitivamente a essa pergunta
(portanto em nível básico) tanto do ponto de vista
conceitual-operacional quanto do ponto de vista
gráfico.
Começando pelo ponto de vista conceitualoperacional. O cálculo diferencial, cuja operação
matemática correspondente é chamada de
derivada, busca responder a seguinte questão
fundamental: Como uma função varia ponto a
ponto? Ou ainda, de maneira equivalente: Qual a
taxa de variação que uma função apresenta em
função de um determinado parâmetro?
É difícil superestimar a importância dessa
pergunta. Talvez não seja difícil imaginar que
responder como a posição de um corpo varia em
função do tempo é importante para o estudo da
cinemática e que essa variação da posição do
corpo em função do tempo, ou melhor, a taxa de
variação da posição do corpo em função do
tempo tem algo haver com a velocidade do corpo.
Veremos que quanto menor for o intervalo de
tempo considerado mais nos aproximamos do
conceito matemático da derivada que é definido
em termos de um processo de limite.
Graficamente, grosso modo, tudo o que vamos
fazer é sair acompanhando a tangente à função,
ponto-a-ponto, para responder a questão de
como uma função varia em função de um
parâmetro ponto-a-ponto (taxa de variação
instantânea da função). Veremos que quanto
maior for a taxa de variação da função num dado
ponto maior será a inclinação (tangente) da
função naquele ponto.
No estudo do movimento a partir do cálculo
diferencial vemos que encontrar a reta tangente à
função horária da posição em função do tempo e
o problema para encontrar a velocidade de um
objeto num determinado instante envolve
determinar o mesmo tipo de limite. Esse tipo
especial de limite é chamado de derivada e
veremos que pode ser interpretado como uma
taxa de variação ou razão incremental tanto
nas ciências quanto na engenharia. Veremos que
o estudo de cálculo integral relaciona-se ao
processo inverso da derivada (somatória das
áreas).
52
PCNA-FÍSICA ELEMENTAR
CONCEITO
Seja uma função 𝑓(𝑥) qualquer, e sobre ela
Traçamos uma reta que interceptos dois pontos
quaisquer desta função, 𝑓(𝑥). A essa reta,
chamamos de reta secante, conforme segue na
figura 5.2 que mostra como extraímos o fator
coeficiente angular da reta.
𝒎𝒙 =
𝒇(𝒙+𝒉)−𝒇(𝒙)
𝒉
(5.5)
Substituindo temos:
𝒗𝒎𝒙 =
𝒙𝟐 − 𝒙𝟏 ∆𝒙
=
𝒕𝟐 − 𝒕𝟏
∆𝒕
(𝟓. 𝟔)
Agora, aproximando o ponto ‘x2’ do ponto ‘x1’, o
próprio
∆𝒕
se
aproxima
de
zero
e
consequentemente a reta secante vai se
aproximando de uma reta tangente no ponto P1,
ou seja, numa reta que intercepta a função
somente neste ponto, além de ser “rente” ao
gráfico se torna uma reta tangente e que o
coeficiente angular dessa reta é a velocidade
instantânea.
Figura 5.2 - Reta secante a uma função f(x)
IMPORTANTE!
A reta secante a uma curva é uma reta que cruza
dois ou mais pontos desta mesma curva e o
coeficiente angular da reta secante acima é dado
pela fórmula da geometria analítica:
𝒎=
𝒇(𝒙+𝒉)−𝒇(𝒙)
𝒉
(5.4)
Note que a equação (5.4) quando aplicado à
cinemática, nos fornece uma equação conhecida
que é a velocidade média. Em outras palavras,
podemos afirmar que velocidade média é a
inclinação de uma reta secante como podemos
ver na Figura 5.3.
Figura 5.4 - Reta secante tendendo a uma tangente
Vemos que a Reta tangente a uma curva é a reta
que intercepta essa mesma curva em somente
um ponto, ou seja, mx = inclinação da reta
tangente.
𝒎𝒙 = 𝐥𝐢𝐦
𝒇(𝒙+𝒉)−𝒇(𝒙)
𝒉
𝒉→𝟎
Substituindo temos:
𝒗𝒙 = 𝐥𝐢𝐦
∆𝒙
∆𝒕→𝟎 ∆𝒕
=
𝒅𝒙
𝒅𝒕
(5.7)
(5.8)
Em outras palavras podemos dizer que quando
“h”
tende a zero, o valor da inclinação da reta
secante tende ao valor da inclinação da reta
tangente.
Figura 5.3 – Gráfico de posição no tempo.
Logo a velocidade média em ‘x’ é dada pelo
coeficiente angular da reta secante a curva como
segue abaixo:
53
PCNA-FÍSICA ELEMENTAR
Então:
IMPORTANTE!
Através da
instantânea.
expressão
∆𝒙
𝒗𝒙 = 𝐥𝐢𝐦
∆𝒕→𝟎 ∆𝒕
Onde
da
=
𝒅𝒙
velocidade
(5.9)
𝒅𝒕
𝒅𝒙
é a taxa de variação com a qual a
𝒅𝒕
posição x está variando com o tempo t
podemos ver isso de forma clara em um
velocímetro de um automóvel.
5.7 Aceleração Média x Aceleração Escalar Média
Qual é a diferença entre aceleração média e
aceleração escalar média?
A diferença é que aceleração média é uma
grandeza vetorial e aceleração escalar média é a
intensidade ou magnitude dessa grandeza
vetorial.
Quando a velocidade de uma partícula varia, dizse que a partícula foi acelerada. Para
movimentos ao longo de um eixo, a aceleração
média, em um intervalo de tempo ∆t é:
⃗⃗⃗⃗⃗𝒎 =
𝒂
⃗⃗⃗⃗
𝒗𝟐 − ⃗⃗⃗⃗
𝒗𝟏
𝒕𝟐 − 𝒕𝟏
=
⃗
∆𝒗
∆𝒕
(5.10)
̅𝟏 no
Para a partícula que tem velocidade 𝒗
instante 𝒕𝟏 e velocidade ̅̅̅̅
𝒗𝟐 e no instante 𝒕𝟐 e
onde a unidade no SI de aceleração é metros
por segundo ao quadrado (m/s²).
𝒂=
𝒅²𝒙
(5.13)
𝒅𝒕²
Ou seja, a aceleração de uma partícula em
qualquer instante é a derivada segunda da
posição x(t) em relação ao tempo. A aceleração
também é uma grandeza vetorial.
IMPORTANTE!
Tome
cuidado
para
não
confundir
aceleração com velocidade! A velocidade
indica como a posição de um corpo varia
com o tempo e é um vetor cujo módulo
indica a velocidade da variação de
deslocamento do corpo e sua direção e
sentido mostram a direção e sentido do
movimento. Já a aceleração depende de
como o vetor velocidade varia em relação ao
tempo.
PROPRIEDADES DA DERIVADA
DERIVADA DE UMA CONSTANTE k
𝒌′ = 𝟎
(5.14)
O leitor pode estar se perguntando: Por que a
derivada de uma função constante é igual à zero?
Bem, o que caracteriza uma função constante é
que independentemente do valor que a variável
assume, o valor da função permanece o mesmo,
ou seja, a taxa de variação é igual à zero para a
função abaixo conforme a Figura 5.5.
5.8 ACELERAÇÃO INSTANTÂNEA
Também chamada de aceleração pode ser
definida seguindo o mesmo procedimento
adotado
quando
definimos
velocidade
instantânea. Portanto, temos que:
𝒂 = 𝐥𝐢𝐦
∆𝒗
∆𝒕→𝟎 ∆𝒕
=
𝒅𝒗
𝒅𝒕
Figura 5.5 - Reta horizontal de uma função constante
(5.11)
Como podemos ver que a velocidade instantânea
é dada por:
𝒗=
𝒅𝒙
𝒅𝒕
(5.12)
Vimos que a derivada nada mais é do que a
taxa de variação da função. Para o caso da
função constante, a resposta da pergunta “Como
varia a função em termos de x?” é simples. A
função permanece constante, ou seja, não varia.
Portanto só relembrando a taxa de variação da
função em termos de x, ou seja, a derivada é
igual à zero.
54
PCNA-FÍSICA ELEMENTAR
DERIVADA DE UMA FUNÇÃO POTÊNCIA EM X
(𝒙𝒏 )′ = 𝒏. 𝒙𝒏−𝟏 (5.15)
Obs. Para qualquer 𝒏 real diferente de zero.
Escolhemos fornecer a regra da derivada para a
função potência, pois uma grande variedade de
fórmulas importantes para a física é descrita por
esse tipo de função (também conhecida como
função polinomial). Por exemplo, veremos que no
estudo do movimento em uma dimensão que a
posição de um objeto em função do tempo pode
ser descrita da seguinte forma:
𝒙 = 𝒙𝒐 + 𝒗𝒐 𝒕 + 𝒂
𝒕𝟐
(5.16)
𝟐
Como podemos encontrar a velocidade
instantânea em função do tempo para a função
acima?
Veremos a seguir os procedimentos a ser feito
para se determinar a velocidade instantânea e a
sua aceleração instantânea em função do tempo
através da regra de soma ou a subtração das
derivadas das funções.
SOMA OU SUBTRAÇÃO
𝒇(𝒕) = 𝒖(𝒕) ± 𝒗(𝒕)
𝒇′ (𝒕) = 𝒖′ (𝒕) ± 𝒗′ (𝒕) (5.17)
função e em seguida substituímos na derivada
da função o ponto específico no qual estamos
interessados.
Com base no conhecimento adquirido até aqui,
usando a derivada, calcule a velocidade
instantânea e a aceleração instantânea da
seguinte expressão:
𝒙 = 𝒙𝒐 + 𝒗𝒐 𝒕 + 𝒂
𝒕𝟐
𝟐
Em seguinte verifique se a velocidade e a
aceleração dependem do tempo e reflita sobre os
resultados obtidos.
ANÁLISE DA DERIVADA
A derivada é uma ferramenta muito poderosa que
nos diz se uma função é crescente ou não em um
determinado ponto. Isso é possível analisando-se
o sinal da derivada da função neste ponto,
conforme a regra abaixo:
f’(xo) >0: A função f é crescente em x=xo;
f’(xo) <0: A função f é decrescente em x=xo;
f’(xo) =0: x=xo é um ponto crítico de f.
As duas primeiras afirmações podem ser
constatadas pela figura a seguir sobre aspectos
importantes:
A derivada da soma (subtração) é igual à soma
(subtração) das derivadas.
CONSTANTE k MULTIPLICANDO A FUNÇÃO
′
(𝒌𝒇(𝒕)) = 𝒌𝒇′ (𝒕) (5.18)
IMPORTANTE!
A
derivada
obedece,
portanto,
à
propriedade da distributividade para a soma
e subtração. Ou seja, para calcular a
derivada de uma função com dois ou mais
termos, derive cada um dos termos e
depois some tudo. A regra exposta em 5.7
expõe que a derivada de uma função f(t)
multiplicada por k é igual a derivada de f(t)
vezes k. Ou seja, a constante fica
“esperando” para ser multiplicada pelo
resultado da derivada de f(t).
Sendo a derivada igual à taxa de variação de
uma função em termos do parâmetro do qual ela
depende. A pergunta de interesse é o quanto
varia a função em um ponto específico. Para
isso procedemos da seguinte forma: Derivamos a
Figura 5.6 - Derivada indicando se f é crescente ou
decrescente.
De outra forma, percebe-se que uma função é
crescente em xo se a reta tangente à função em
xo está “subindo”, e “mergulhando” em direção ao
eixo x para o caso decrescente.
Para o caso de f’(xo) =0, como já visto, diz-se que
xo é um ponto crítico de f. Um ponto crítico é
basicamente um ponto cuja derivada é nula ou
não existe. Intuitivamente, os pontos que anulam
a derivada são ditos máximos ou mínimos locais
de uma função, já que a reta tangente a eles é
horizontal e, portanto tem coeficiente angular
igual à zero, conforme figura abaixo:
55
PCNA-FÍSICA ELEMENTAR
tensão induzida através da taxa de variação do
fluxo magnético com o tempo.
𝑓𝑒𝑚 = −
Figura 5.7 - Na figura acima, c é máximo local e d é
mínimo local (f’(c)=f’(d)=0)
Um ponto de máximo local pode ser definido
como o “cume da montanha”, ou seja, é um ponto
cuja imagem (f(c)) é maior que as imagens dos
pontos imediatamente à esquerda e à direita de c
(c-0,00001
e
c+0,00001,
por
exemplo).
Explicação análoga vale para o mínimo local
(“vale da montanha”).
𝑑𝛹
𝑑𝑡
Sem contar com as aplicações da derivada na
medicina, biologia, economia e outras áreas do
conhecimento. Portanto, podemos perceber a
grandiosidade e aplicabilidade dessa valiosa
ferramenta que é o calculo diferencial.
Observando a Figura 5.7, percebemos que o
caminho de “ida” a partir da posição para a
velocidade e posteriormente para a aceleração,
nós sabemos! Agora como fazer o caminho de
“volta”?
IMPORTANTE!
O estudo dos máximos e mínimos de uma
função é uma das aplicações mais
importantes da derivada para um
engenheiro, o qual usa essa ferramenta,
entre outras finalidades, para minimizar o
custo de seus projetos.
APLICAÇÕES DO CÁCULO DIFERENCIAL
O calculo diferencial ou simplesmente derivada é
encontrado nos mais diversos ramos da física e
engenharia.
Podemos encontrar na 2º Lei de Newton com
mais sofisticação, como sendo a taxa de variação
do momento linear com o tempo.
𝑑𝑃⃗
𝐹=
𝑑𝑡
Encontramos na definição de potência como taxa
de variação de energia com o tempo
𝑃=
Figura 5.8 – Tabela representativa de derivada e
integral de modo sintético.
Antes de se depararmos com a ferramenta
matemática de imensa aplicabilidade na
engenharia que é cálculo integral aplicado na
cinemática, iremos abordar pontos importantes
das equações usadas no ensino médio quando
temos uma aceleração constante; as equações
que conhecemos do ensino médio como segue
abaixo:
𝒕𝟐
𝒙 = 𝒙𝒐 + 𝒗𝒐 𝒕 + 𝒂
𝟐
𝒗 = 𝒗𝟎 + 𝒂𝒕
𝒗² = 𝒗𝒐 ² + 𝟐𝒂∆𝒙
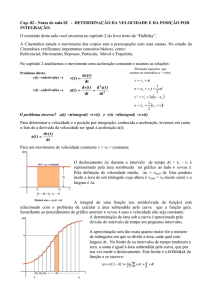
Se analisarmos um gráfico com aceleração
constante temos:
𝑑𝑈
𝑑𝑡
Na engenharia elétrica, podemos encontrar na
simples definição de tensão e corrente, temos:
𝑖=
𝑑𝑞
𝑑𝑡
𝑣=
𝑑𝑤
𝑑𝑞
Outro exemplo da aplicação da derivada
encontra-se na engenharia de telecomunicações
com a famosa Lei de Faraday em campos
variantes no tempo, onde podemos obter a
Figura 5.9 – Gráfico de aceleração no tempo.
56
PCNA-FÍSICA ELEMENTAR
Com a aceleração constante podemos traçar o
gráfico v x t e encontrar o espaço total.
‘’A integração é uma adição sofisticada. É a modo
de processo de pegar uma forma cuja área você
não pode determinar diretamente, cortar em
pequenos pedaços cujas áreas você pode
determinar, e depois somar todos os pedaços
para obter a área do todo. ’’ (Cálculo para
Leigos).
CONCEITO DE INTEGRAL
O conceito de integral está bastante relacionado
à noção de áreas. Os povos gregos se
perguntavam na Antiguidade: “como calcular a
área de uma figura qualquer, como mostra a
Figura 5.12”?
Figura 5.10 – Gráfico da velocidade no tempo
Agora façamos a seguinte pergunta, e se a
aceleração não for constante? Ou seja, se a
aceleração depender do tempo como poderemos
encontrar a velocidade e o espaço?
Nessa configuração que citamos o gráfico, em
termos puramente expositivos é:
Figura 5.12 – Gráfico de uma curva qualquer.
Figura 5.11 - Gráfico da aceleração no tempo.
Por não se tratar de um problema simples a
obtenção dessa área, apropriamo-nos de um
método matemático chamado integral.
Como a curva da figura acima não pertence às
figuras clássicas, como quadrado, triângulo e
círculo, não são possíveis calcular sua área com
fórmulas “prontas” da geometria.
Bom, mas existe uma figura geométrica cuja área
é bem conhecida na geometria: o retângulo. Sua
área pode ser calculada pelo produto da base
com a altura. Numa tentativa de calcular a área
da figura acima, poderíamos desenhar vários
retângulos cujas alturas são determinadas pela
própria figura, como segue:
5.9 NOÇÕES DO CALCULO INTEGRAL
A integral é um recurso matemático inverso ao da
𝑑𝑦
derivada, ou seja, ao invés de achar derivada
𝑑𝑥
de uma função f(x), calcula-se a função f(x) a
𝑑𝑦
partir da derivada da função
, ou seja, também
𝑑𝑥
é conhecida como Anti-Derivada.
Figura 5.13 - Curva sendo aproximada
grosseiramente por retângulos.
57
PCNA-FÍSICA ELEMENTAR
Como se vê, a aproximação não é perfeita, mas
quanto menores serem às bases desses
retângulos, mais próxima à soma de suas áreas
vai ficar em relação à área A desejada, como
podemos ver na Figura 5.14 a seguir.
INTEGRAL DE UMA CONSTANTE K
∫ 𝒌𝒅𝒙 = 𝒌𝒙 + 𝒄 (5.19)
INTEGRAL DE UMA FUNÇÃO POTÊNCIA EM X
∫ 𝒙𝒏 𝒅𝒙 =
𝒙𝒏+𝟏
𝒏+𝟏
+ 𝒄 (5.20)
Para qualquer n ≠ -1
Obs.: Se n = -1, sua integral será dada pela
função logarítmica 𝐥𝐧(𝒙) + 𝒄, ou seja, temos:
∫ 𝒙−𝟏 𝒅𝒙 = ∫
𝒅𝒙
= 𝐥𝐧(𝒙) + 𝒄 (5.21)
𝒙
SOMA OU SUBTRAÇÃO
𝒇(𝒙) = 𝒖(𝒙) ± 𝒗(𝒙)
Figura 5.14 - Aproximação melhorada com o uso de
retângulos mais finos
IMPORTANTE!
A ideia da integral é que a área de uma figura
qualquer é aproximada pela soma das áreas
de incontáveis retângulos de espessura
praticamente nula. Daí pode-se considerar a
integral
um
processo de soma de
pequeníssimas parcelas, que seriam as áreas
de cada retângulo, até chegar ao total
esperado (área A da Figura 5.14).
NOTAÇÃO
A integral de uma função f(x) é denotada por
∫ 𝒇(𝒙)𝒅𝒙, onde

se assemelha a um S
estendido, de soma. Tal qual fizemos em relação
à derivada, vamos colocar algumas propriedades
da integral.
IMPORTANTE!
As propriedades de distributividade da
soma e da multiplicação de uma integral
por uma constante são mantidas na
integração, tal como na operação de
diferenciação.
PROPRIEDADES DA INTEGRAL
Assim como na seção derivadas, f, u e v são
funções de x. c é uma constante arbitrária que
aparece no processo de integração.
∫ 𝒇(𝒙)𝒅𝒙 = ∫ 𝒖(𝒙)𝒅𝒙 ± ∫ 𝒗(𝒙)𝒅𝒙 (5.22)
A integral da soma (subtração) é igual à soma
(subtração) das integrais.
CONSTANTE MULTIPLICANDO UMA FUNÇÃO
∫ 𝒌𝒇(𝒙)𝒅𝒙 = 𝒌 ∫ 𝒇(𝒙)𝒅𝒙 (5.23)
IMPORTANTE!
Como se podem perceber, essas duas
últimas propriedades da integral são
análogas às da derivada.
.
5.10 APLICAÇÃO NA CINEMÁTICA
A derivada foi usada para obter a velocidade
instantânea a partir do espaço e a aceleração
instantânea a partir da velocidade instantânea. Já
que a integral é o processo inverso da derivada,
como dito no início do capítulo, era de se esperar
que a integral fosse usada para calcular a
variação de espaço em função da velocidade
instantânea e a velocidade instantânea a partir da
aceleração
instantânea.
Essa
suposição,
felizmente, é verdadeira, da qual vêm as
equações:
∆𝑺 = ∫ 𝒗𝒊𝒏𝒔𝒕𝒂𝒏𝒕𝒂𝒏𝒆𝒂 𝒅𝒕 (5.24)
𝒗𝒊𝒏𝒔𝒕𝒂𝒏𝒕𝒂𝒏𝒆𝒂 = ∫ 𝒂𝒊𝒏𝒔𝒕𝒂𝒏𝒕𝒂𝒏𝒆𝒂 𝒅𝒕 (5.25)
58
PCNA-FÍSICA ELEMENTAR
Ora, se a integral de uma grandeza é igual à área
do gráfico dessa mesma grandeza, então se nos
for apresentado um gráfico da velocidade
instantânea em relação ao tempo (v x t), sua área
entre dois instantes t1 e t2 será igual à variação de
espaço ocorrida entre esses mesmos instantes. A
Figura 5.15 a seguir exemplifica melhor essa
ideia.
Figura 5.15 - A variação no espaço é igual à área do
gráfico v x t
Embora possa parecer estranho obter o espaço
percorrido a partir de um gráfico da velocidade
em função do tempo, fizemos isso sem perceber
quando resolvíamos problemas de cinemática no
ensino médio. O mesmo raciocínio vale para a
velocidade instantânea. Por ser a integral da
aceleração no tempo, pode ser calculada também
como a área do gráfico da aceleração versus
tempo(axt):
RESUMO DAS PRINCIPAIS ÊNFASES DO
CAPÍTULO:
 Gráficos trazem informações importantes e
precisamos relacionar essas informações
com base nos conceitos que estamos
estudando. Neste capítulo fizemos a extração
da informação a partir de gráficos da
cinemática e relacionamos a informação com
as ferramentas básicas do cálculo diferencial
e integral.
 Seja o problema de determinar a taxa de
variação de uma função ponto-a-ponto ou
calcular a área de um gráfico delimitada por
uma dada função em certo intervalo,
precisamos
prestar
atenção
na
dimensionalidade da taxa de variação e na
dimensionalidade da área que estamos
trabalhando.
 Cálculo diferencial (a derivada) e o cálculo
integral
(a
integral)
são
operações
matemáticas inversas. Isso quer dizer que
atuar com uma das duas operações
matemáticas sobre a função e em seguida
atuar com a outra operação, o efeito da
primeira é anulado. Isso nos “devolve” a
função original. Esse é, grosso modo, o que
quer dizer operações matemáticas serem
inversas.
Figura 5.16 - A variação na velocidade é igual à área
do gráfico a x t
59