Velocidade e Aceleração Instantânea

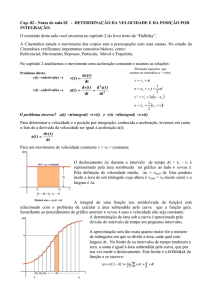
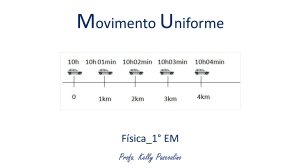
2ª Aula do cap.2
Velocidade Instantânea e
Aceleração Instantânea
Introdução
Velocidade Média e Velocidade Instantânea.
Aceleração Média e Aceleração Instantânea.
Velocidade Média e Velocidade escalar.
Limite de uma função.
Referência:
Halliday, David; Resnick, Robert & Walker, Jearl. Fundamentos de Física, Vol 1.
Cap. 04 da 7a. ed. Rio de Janeiro: LTC, 1996.
Tipler, Paul. Física, Vol 1 cap. 03. 4a. ed. Rio de Janeiro: LTC, 2000.
http://geocities.yahoo.com.br/saladefisica3/laboratorio/movimentos/movimentos.htm
O Deslocamento e Velocidade média
Deslocamento, variação de espaço de (x1,t1) para (x2,t2).
Exemplo: corrida de 100 metros.
Δx = x2 - x1
Δx = x2 - x1
Δt = t2 - t1
(independe do
caminho)
Velocidade média
Ouro - Justin Gatlin
↳
v med
x 2 − x1 Δx
=
=
t 2 − t1
Δt
de 0s até 5.01s:
vmed = 40m / 5.01s = 8.0 m/s
de 5.01s até 10.5s:
vmed = 60m / 5.49s = 10.9 m/s
Velocidade Instantânea
Conceito
Δx dx
=
v(t ) = lim
Δt → 0
Δt
dt
Exemplo:
Na corrida, de 100 m,
a velocidade em t = 2s é
90m
v( t = 2s) =
= 8.0 m s
11.2s
Derivada
Geometricamente
Tangente
Velocidade média
Velocidade instantânea
Aceleração Média
a med
v 2 − v1 Δv
=
=
t 2 − t1
Δt
A corredora acelera uniformemente
até 10m/s em t =4s. Mantêm a
velocidade nos próximos 4s.
De 8s até 12.7s reduz a velocidade
para 8m/s.
de 0s até 4s:
amed = 10m/s / 4s = 2.5 m/s2
de 4s até 8s:
amed = 0m/s / 4s = 0 m/s2
de 8s até 12.7s: amed = -2m/s / 4.7s = -0.42 m/s2
Gráficos
Aceleração Instantânea
Conceito
√
√
Derivada
Δv dv
=
a = lim
Δt →0 Δt
dt
note
dv d ⎡ dx ⎤ d 2 x
a=
= ⎢ ⎥= 2
dt dt ⎣ dt ⎦ dt
Exemplo:
Na corrida, de 100 m,
a aceleração em t = 2s é
a ( t = 2s) =
5.9 m s
= 2.2 m s 2
2.7s
Segunda
derivada
Resumo dos Conceitos:
Velocidade Instantânea e Aceleração Instantânea
• Problema direto,
– x(t) →(derivada) → v(t)
– v(t) →(derivada) → a(t)
• Problema inverso ???
– a(t) →(integral) → v(t)
– v(t) →(integral) → x(t)
• Quem fez?
As equações de movimento para o
caso de aceleração constante são:
v = v 0 + at
1 2
x = x 0 + v 0 t + at
2
v 2 = v 02 + 2a (x − x 0 )
1
x = x 0 + (v 0 + v )t
2
Sir Isaac Newton (1642 – 1727)
Resumo dos Conceitos:
• Problema direto,
– x(t) →(derivada) → v ( t ) = dx ( t )
dt
Sir Isaac Newton (1642 – 1727)
2
dv ( t ) d x ( t )
=
– v(t) →(derivada) → a ( t ) =
2
dt
dt
•Problema inverso ???
– integral→ a(t)
– integral → v(t)
v ( t ) = ∫ a ( t )dt
x ( t ) = ∫ v ( t )dt
Exemplo:
Velocidade Instantânea
Posição dada por x(t) = 5 t2