Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 36 – A LEI DA INDUÇÃO DE FARADAY
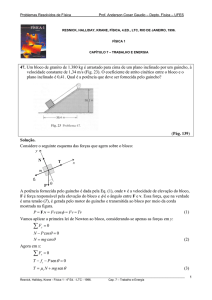
37. Um bastão com comprimento L, massa m e resistência R desliza sem atrito sobre dois trilhos
paralelos condutores de resistência desprezível, como ilustra a Fig. 49. Os trilhos estão
conectados na parte inferior, formando uma espira condutora onde o bastão é a parte superior. O
plano dos trilhos faz um ângulo θ com a horizontal e existe um campo magnético uniforme
vertical B na região onde está o dispositivo. (a) Mostre que o bastão adquire uma velocidade
limite cujo módulo é
v=
mgR sen θ
B 2 L2 cos 2 θ
(b) Mostre que a taxa com que a energia interna está sendo gerada no bastão (efeito Joule) é
igual à taxa com que o bastão está perdendo energia potencial. (c) Discuta a situação se B fosse
orientado para baixo, ao invés de para cima.
(Pág. 194)
Solução.
(a) A velocidade limite será atingida quando a força de frenagem Ff (componente da força
magnética ao longo dos trilhos) sobre o bastão for igual à força que acelera o bastão rampa abaixo
Fa (componente da força peso do bastão ao longo dos trilhos).
Ff = Fa
(1)
Para resolver este problema, precisamos encontrar expressões para essas duas forças e substitui-las
em (1). Considere o esquema abaixo:
B
θ dA
F θ
iL
θ
P θ
Em primeiro lugar vamos determinar a força de frenagem Ff. A força magnética que age sobre a
barra é dada por:
F= iL × B
x
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 36 – A Lei da Indução de Faraday
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
F = iLB
A força de frenagem é a componente de F paralela à rampa e vale:
=
Ff F=
cos θ iLB cos θ
(2)
O fluxo do campo magnético através do circuito vale:
=
Φ
B.dA
∫=
BA=
cos θ BLx cos θ
Logo, a fem no circuito é obtida por meio da lei da indução de Faraday:
dΦ
=
ε = BLv cos θ
dt
A corrente na barra vale:
ε BLv cos θ
i =
=
R
R
Substituindo-se (3) em (2):
 BLv cos θ
Ff = 
R

(3)

 BL cos θ

B 2 L2 v cos 2 θ
R
Em segundo lugar vamos determinar a força que acelera a barra rampa abaixo:
=
Fa P=
sen θ mg sen θ
Ff =
(4)
(5)
Finalmente podemos substituir (4) e (5) em (1):
B 2 L2 v cos 2 θ
= mg sen θ
R
mgR sen θ
v= 2 2
B L cos 2 θ
(b) A potência dissipada por efeito Joule é dada por:
BLv cos θ
P=
ε=i BLv cos θ .
J
R
B 2 L2 v 2 cos 2 θ
PJ =
R
A taxa de perda de energia potencial gravitacional vale:
mgR sen θ
PG F=
mg sen θ . 2 2
=
av
B L cos 2 θ
=
PG
m 2 g 2 R sen 2 θ
B 2 L2 cos 2 θ
(6)
 RB 2 L2 cos 2 θ 
× 2 2

2
 RB L cos θ 
 m 2 g 2 R 2 sen 2 θ  B 2 L2 cos 2 θ
PG =  4 4

4
R
 B L cos θ 
Na equação acima, o termo entre parênteses é v2 (resultado do item (a)). Logo:
B 2 L2 v 2 cos 2 θ
R
A igualdade entre (6) e (7) completa a demonstração.
PG =
(7)
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 36 – A Lei da Indução de Faraday
2
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
(c) Caso o campo magnético fosse invertido, em nada alteraria o sentido das forças. Isso ocorre por
causa da inversão do sentido da corrente elétrica no circuito, que é uma conseqüência da lei de
Lenz.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 36 – A Lei da Indução de Faraday
3