Impulso e quantidade de movimento

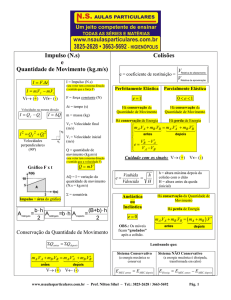
IMPULSO E QUANTIDADE
DE MOVIMENTO
Prof.: Henrique Dantas
Impulso
É a grandeza física vetorial relacionada com a
força aplicada em um corpo durante um intervalo
de tempo.
O impulso é dado pela expressão:
 
I  F .t
I = impulso (N.s);
F = força (N);
Δt = tempo de atuação da força F (s).
Impulso
Ao empurrarmos um carro, por exemplo, quanto maior a
intensidade da força e o tempo de atuação dessa força,
maior será o impulso aplicado no carro.
O Impulso é uma grandeza vetorial que possui a mesma
direção e sentido da força aplicada.
 
I  F .t
Impulso
Canhões de longo alcance possuem canos compridos.
Quanto mais longo este for, maior a velocidade
emergente da bala.
Isso ocorre porque a força gerada pela explosão da
pólvora atua no cano longo do canhão por um tempo
mais prolongado. Isso aumenta o impulso aplicado na
bala do canhão.
O mesmo ocorre com os rifles em relação aos
revólveres.
Impulso
Quando a força aplicada não for constante ao longo do
tempo, a intensidade do impulso pode ser calculada
através da Área do gráfico F x t com o eixo do tempo,
conforme a seguir.
I = Área
|F|
A
t1
t2
t
Curiosidade:
Hoje, constantemente vemos nos veículos de comunicação que
tem crescido o número de acidentes de trânsito, sejam eles
provocados por falhas humanas, pela falta de conservação de
estradas ou por falhas mecânicas dos automóveis. O que
vemos é que cada vez mais a indústria automobilística está
sendo forçada, tanto por medidas reguladoras dos governos
quanto por questões de marketing, a adotar mecanismos de
segurança que possam proteger de forma mais adequada os
passageiros dos veículos em casos de colisão.
Se observarmos bem, as medidas mais comuns que as
indústrias estão tomando são em relação à construção de
carros com estruturas mais seguras, como AIRBAGS,
cintos de segurança mais reforçados, eficientes e assentos
mais seguros.
Como funcionam os airbags
Curiosidade:
Quando um carro colide contra um muro de pneus, o
tempo de frenagem é aumentado devido à deformação
sofrida. Isso diminui a violência do impacto, fazendo
com que a variação da quantidade de movimento não
seja tão abrupta, diminuindo assim a força média
envolvida na colisão.
Imagem: Royalbroil / Creative Commons Attribution-Share Alike 3.0 Unported.
Curiosidade:
Qual o carro mais seguro? O carro antigo, que usava
materiais mais resistentes aos choques, ou os atuais,
que utilizam outros materiais na sua fabricação, como
plásticos?
Imagem: Thue / Domínio Público.
Numa colisão o parachoque e
a carroceria do carro devem
se
deformar o máximo
possível, para diminuir os
efeitos
da
colisão
nos
passageiros. Como o intervalo
de tempo aumenta, a variação
da quantidade de movimento
será menos abrupta, com isso
diminuindo a força média
durante a colisão.
Quantidade de Movimento
Todos nós sabemos que é muito mais difícil parar
um caminhão pesado do que um carro que esteja
se movendo com a mesma rapidez.
Isso se deve ao fato do caminhão ter mais inércia
em
movimento,
movimento.
ou
seja,
quantidade
de
Quantidade de Movimento
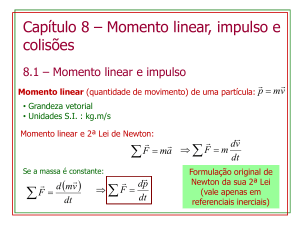
É a grandeza física vetorial relacionada com a massa de
um corpo e sua velocidade.
A quantidade de movimento, ou momento linear, é dada
pela expressão:


Q  m.v
Q = quantidade de movimento (kg.m/s);
m = massa (kg);
v = velocidade (m/s).
Quantidade de Movimento
A quantidade de movimento é uma grandeza vetorial
que
possui
a
mesma
direção
e
sentido
da
velocidade.
As unidades (dimensões) de Impulso e Quantidade
de Movimento são equivalentes:
m
[ I ]  N .s  kg. 2 .s  kg.m / s  [Q]
s
Teorema do Impulso
Considere um corpo de massa m que se desloca em uma
superfície horizontal com uma velocidade vo. Em um certo
instante passa a atuar nele uma força resultante de
intensidade F, durante um intervalo de tempo Δt.
O impulso produzido pela força F é igual a:
I  F.t
V  Vo
a
t
I  m.V  m.Vo
I  m.a.t
F  m.a
 V  Vo
I  m.
 t

.t

Q  m.v
I  m.V  Vo 


I  Q
Teorema do Impulso


I  Q
Para o mesmo intervalo de tempo, o impulso da
força resultante é igual à variação da quantidade de
movimento.
Sistema Isolado de Forças
Considere um sistema formado por dois corpos
A e B que se colidem.
No sistema, as forças decorrentes de agentes
externos ao sistema são chamadas de forças
externas, como, por exemplo o peso P e a
normal N. No sistema, a resultante dessas forças
externas é nula.
Sistema Isolado de Forças
Durante a interação, o corpo A exerce uma força F no
corpo B e este exerce no corpo B uma força -F, de
mesmo módulo e sentido oposto. As forças F e -F
correspondem ao par Ação e Reação.
Denomina-se sistema isolado de forças externas o
sistema cuja resultante dessas forças é nula, atuando
nele somente as forças internas.
Princípio da Conservação da
Quantidade de Movimento
Considerando um sistema isolado de forças
externas:
FR  0
I  FR .t
Pelo Teorema do Impulso
Como
I 0
I 0
I  QF  QI
QI  QF
A quantidade de movimento de um sistema de
corpos, isolado de forças externas, é constante.
QI  QF
Quantidade de movimento
em uma dimensão
++
Observações:
A quantidade de movimento pode permanecer
constante ainda que a energia mecânica varie.
Isto é, os princípios da conservação de energia
e da quantidade de movimento são
independentes.
A quantidade de movimento dos corpos que
constituem o sistema mecanicamente isolado
não é necessariamente constante. O que
permanece constante é a quantidade de
movimento total dos sistema.
Observações:
Durante uma desfragmentação ou explosão o centro
de massa do sistema não altera o seu comportamento.
Colisão Elástica
Observe que, se calcularmos a energia cinética total do
sistema, encontraremos:
Antes da Colisão: EcA + EcB = 8+4 = 12j
Após a Colisão:
EcA + EcB = 5+7 = 12j
Neste caso, a energia cinética total dos corpos que colidiram
se conservou. Esse tipo de colisão, na qual, além da
conservação de movimento (que sempre ocorre), há também a
conservação da energia cinética, é denominada colisão
elástica.
Colisões
As colisões podem ocorrer de duas maneiras
distintas, dependendo do que ocorre com a
energia cinética do sistema antes e depois da
colisão.
1 - Colisão Elástica
2 - Colisão Inelástica
Colisão Elástica
Suponha que duas esferas, A e B, colidissem de tal
modo que suas energias cinéticas, antes e depois da
colisão, tivessem os valores mostrados na figura a
seguir.
Colisão Inelástica (ou Plástica)
É aquela onde a energia cinética não se conserva. Isso
ocorre porque parte da energia cinética das partículas
envolvidas no choque se transforma em energia térmica,
sonora etc.
Não se esqueça, mesmo a energia cinética não se
conservando, a quantidade de movimento do sistema se
conserva durante a colisão.
A maioria das colisões que ocorrem na natureza é
inelástica.
Colisão Perfeitamente
Inelástica
É aquela que, após o choque, os corpos passam a ter a
mesma velocidade (movem-se juntos), tendo a maior
perda possível de energia cinética do sistema.
A figura a seguir exemplifica um colisão perfeitamente
inelástica.
Obs.: na colisão perfeitamente inelástica não se perde,
necessariamente, toda a energia cinética.
Coeficiente de Restituição
O coeficiente de restituição é definido como sendo a
razão entre a velocidade de afastamento e a de
aproximação.
e
Vafast.
Vaprox.
Se um corpo for abandonado de uma altura H e após
o choque com o chão o corpo atingir a altura h,
temos:
e
h
H
Coeficiente de Restituição
O coeficiente de restituição é um número puro (grandeza
adimensional), extremamente útil na classificação e
equacionamento de uma colisão:
Colisão Elástica
vafast. = vaprox.
e=1
Colisão Inelástica
vafast. < vaprox
0<e<1
Colisão Perf. Inelástica
vafast. = 0
e=0
LEMBRE-SE QUE:
 O impulso é uma grandeza vetorial relacionada com uma
força e o tempo de atuação da mesma.
 Quantidade de movimento é uma grandeza vetorial que
possui mesma direção e sentido do vetor velocidade.
 O impulso corresponde à variação da quantidade de
movimento.
 Durante uma colisão (ou explosão) a quantidade de
movimento do sistema permanece constante.
 A quantidade de movimento pode permanecer constante
ainda que a energia mecânica varie.
 Após a colisão perfeitamente inelástica os corpos saem
juntos.