I. Quantidade de movimento

O que você deve saber sobre
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
Com base no senso comum, sabemos que é muito pior colidir com
um caminhão do que com uma bicicleta. Também é intuitivo que
uma batida na qual os veículos envolvidos estejam em baixa
velocidade é muito mais suave do que se eles estiverem correndo.
Para lidar com problemas que envolvam colisões, utilizamos os
conceitos de impulso e quantidade de movimento. Veremos que a
conservação da quantidade de movimento é mais comum e ampla
do que a conservação da energia mecânica.
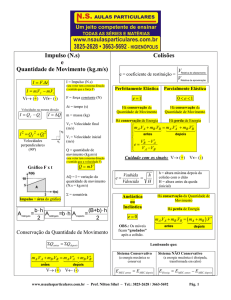
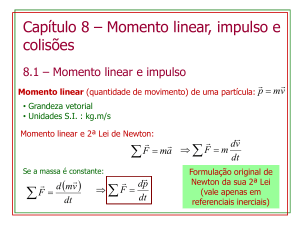
I. Quantidade de movimento
Quantidade de movimento (momento linear) é o vetor Q com as
seguintes características:
• Módulo: é definido pela expressão Q = m . v.
• Direção e sentido: coincidem com os do vetor velocidade instantânea.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
II. Impulso
SEBASTIEN NOGIER/REUTERS/LATINSTOCK
Grandeza física que relaciona a força aplicada a um corpo com o
tempo que dura a interação entre a força e o corpo.
Para conseguir golpes mais fortes, o
tenista procura manter a bola em
contato com a raquete o maior
tempo possível.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
II. Impulso
Força constante
O módulo do impulso é dado por:
Direção e sentido do impulso: coincidem com os da
força F aplicada.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
II. Impulso
Força variável
O impulso é numericamente igual à soma algébrica das áreas entre
o gráfico F x t e o eixo das abscissas.
As áreas sob o eixo contribuem
negativamente para o impulso.
Nesse caso temos:
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
II. Impulso
Impulso: resultado da variação do
movimento provocado pela aplicação
de uma força
No bloqueio, a força exercida pela
jogadora, ao receber uma cortada, altera a
quantidade de movimento da bola e muda sua
direção. Quanto maior o tempo de contato entre a
mão e a bola, maior a força com que esta
retorna ao outro lado da quadra.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
PATRICK STRAUB/EPA/CORBIS/LATINSTOCK
Teorema do impulso
IV. Colisões unidimensionais
MATTHIAS KULKA/ZEFA/CORBIS/LATINSTOCK
Numa colisão mecânica, supondo-se que a massa dos corpos não
se altere, ocorrem duas etapas:
 deformação (a energia cinética dos corpos antes do choque se
transforma em energia potencial elástica, energia sonora – ruído –
e energia térmica – calor);
 restituição (toda ou parte da energia transformada retorna na
forma de energia cinética).
A colisão da bola de boliche
com os pinos é praticamente elástica.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
V. Velocidade relativa em uma dimensão
Para as situações 1 e 2, temos:
Supondo vA > vB, a velocidade relativa
nas situações 3 e 4 será:
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
VI. Quantidade de movimento em uma dimensão
Nas situações 5 e 6, temos:
Nas situações 7 e 8, temos:
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
+
VI. Quantidade de movimento em uma dimensão
Coeficiente de restituição: razão entre o módulo da velocidade
relativa dos corpos posterior à colisão e o anterior à colisão.
 Colisão:
• perfeitamente elástica: e = 1; energia se conserva.
• inelástica (maior perda de energia): e = 0; não ocorre restituição;
corpos permanecem unidos após a colisão.
• parcialmente elástica: 0 < e < 1; restituição de energia parcial.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
EXERCÍCIOS ESSENCIAIS
2
(U. Braz Cubas-SP)
A força que age em um corpo variou segundo o gráfico dado.
O impulso que a força imprimiu ao corpo foi de:
a) 150 N . s.
b) 300 N . s.
RESPOSTA: A
.
c) 40 N s.
d) 20 N . s.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO – NO VESTIBULAR
EXERCÍCIOS ESSENCIAIS
5
(UFC-CE)
Na superfície de um lago congelado (considere nulo o atrito), um
menino de 40 kg empurra um homem de 80 kg.
Se este adquirir a velocidade de 0,25 RESPOSTA: C
m/s, o menino:
a) escorregará, em sentido contrário,
com velocidade igual em módulo.
b) ficará parado.
c) deslizará, em sentido oposto, com
velocidade de 0,50 m/s.
d) deslizará, para trás, com
velocidade de 2 m/s.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO – NO VESTIBULAR
EXERCÍCIOS ESSENCIAIS
7
(UFMS)
Uma esfera de massa m se movimenta sobre um apoio plano horizontal sem atrito com velocidade 
v e choca-se frontalmente

com outra, de massa 2 m, que se movimenta com velocidade -2v.
Sabendo-se que a colisão foi inelástica, a velocidade do conjunto
constituído pelas duas esferas será:

a) – 2 v .
2
RESPOSTA: D

b) – 2 3v .
4

c) – v .
3
v.
d) – 
e)

v .
3
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO – NO VESTIBULAR
EXERCÍCIOS ESSENCIAIS
13
(Ufes)
Um bloco A é lançado em um plano horizontal com
velocidade de módulo vA = 4,0 m/s. O bloco A tem
massa mA = 2,0 kg e colide frontalmente com uma
esfera B de massa mB = 5,0 kg. Inicialmente, a esfera
encontra-se em repouso e suspensa por um fio ideal de
comprimento L, fixo em O, como mostra a figura ao
lado. Após a colisão, a esfera atinge uma altura máxima
de hB = 0,20 m. Os atritos do bloco A e da esfera B com
a superfície são desprezíveis.
RESPOSTA:
Com essas informações:
a) determine o módulo da velocidade
da esfera B, imediatamente após a
colisão;
b) determine o módulo e o sentido da
velocidade do corpo A, após a colisão;
c) determine a diferença entre a
energia cinética do sistema, antes e
após a colisão;
d) responda se a colisão foi ou não
perfeitamente elástica. Justifique
a sua resposta.
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO – NO VESTIBULAR