Exercícios - Angelfire

Pindyck & Rubinfeld, Capítulo 9, Mercados Competitivos :: EXERCÍCIOS
1. Em 1996, o Congresso dos EUA discutiu se o salário mínimo deveria subir
de $4,25 para $5,15 por hora. Algumas pessoas sugeriram que um subsídio do
governo concedido aos empregadores poderia ajudar a financiar os salários
mais elevados. Este exercício examina o aspecto econômico de um salário
mínimo e de subsídios de salário. Suponha que a oferta de mão de obra não
qualificada seja expressa pela equação
L
S
= 10w
onde LS é a quantidade de trabalho não qualificado (em milhões de pessoas
empregadas a cada ano) e w é o salário (em dólares por hora). A demanda por
trabalho é dada por
L
a.
D
= 80 - 10w .
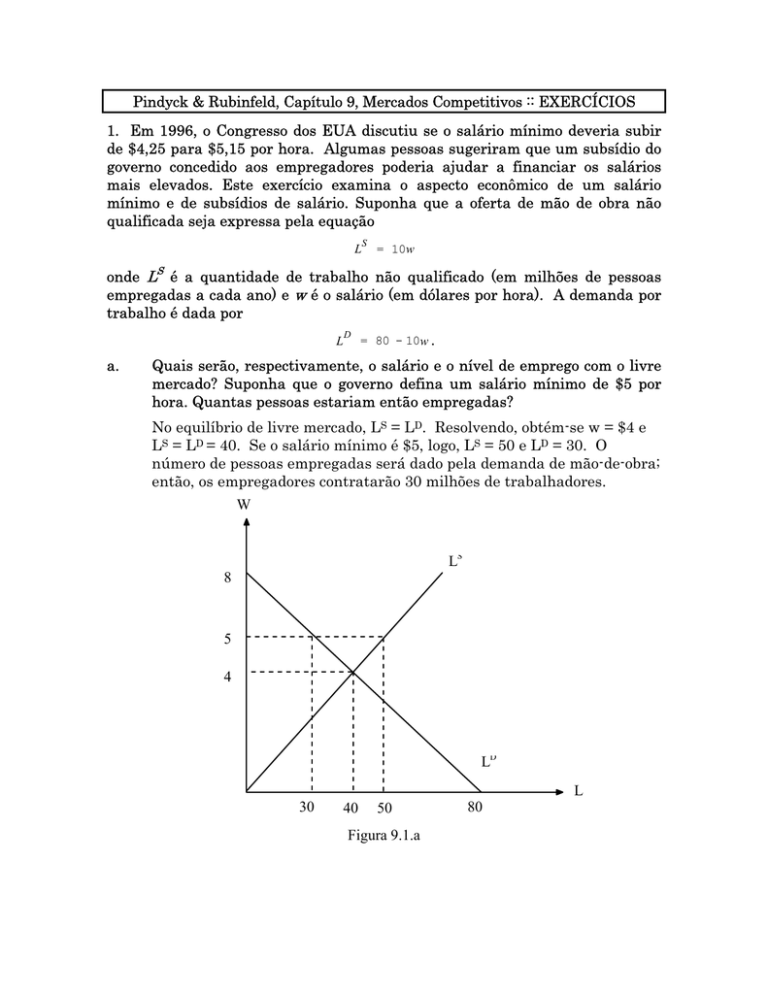
Quais serão, respectivamente, o salário e o nível de emprego com o livre
mercado? Suponha que o governo defina um salário mínimo de $5 por
hora. Quantas pessoas estariam então empregadas?
No equilíbrio de livre mercado, LS = LD. Resolvendo, obtém-se w = $4 e
LS = LD = 40. Se o salário mínimo é $5, logo, LS = 50 e LD = 30. O
número de pessoas empregadas será dado pela demanda de mão-de-obra;
então, os empregadores contratarão 30 milhões de trabalhadores.
W
LS
8
5
4
LD
30
40
50
Figura 9.1.a
80
L
b.
Suponha que, em vez de definir um salário mínimo, o governo pagasse um
subsídio de $1 por hora a cada empregado. Qual seria agora o nível total
de emprego? Qual seria o salário de equilíbrio?
Seja w o salário recebido pelo empregado. Então, o empregador,
recebendo o $1 de subsídio por hora trabalhada, paga apenas w-1
para cada hora trabalhada. Como mostrado na Figura 9.1.b, a
curva de demanda de trabalho se desloca para:
LD = 80 - 10 (w-1) = 90 - 10w,
onde w representa o salário recebido pelo empregado.
O novo equilíbrio será dado pela interseção da curva de oferta
original com a nova curva de demanda, ou seja, 90-10W** = 10W**,
ou W** = $4,5 por hora e
L** = 10(4,5) = 45 milhões de pessoas empregadas.
s
W
L = 10w
9
salário e emprego
após o subsídio
8
4.5
4
L
D
(subsídio)
= 90-10w
D
L = 80-10w
40
45
80
90
L
Figura 9.1.b
2. Suponha que o mercado de um certo bem possa ser expresso pela seguintes
equações:
Demanda: P = 10 - Q
Oferta: P = Q - 4
onde P é o preço em dólares por unidade e Q é a quantidade em milhares de
unidades.
a.
Quais são, respectivamente, o preço e a quantidade de equilíbrio?
O preço e a quantidade de equilíbrio podem ser encontrados
igualando a oferta à demanda e resolvendo, primeiro, para QEQ:
10 - Q = Q - 4, ou QEQ = 7.
e, em seguida, inserindo o valor calculado de QEQ na equação de
demanda ou na equação de oferta para obter PEQ.
ou
b.
PEQ = 10 - 7 = 3,
PEQ = 7 - 4 = 3.
Suponha que o governo crie um imposto de $1 por unidade a fim de
reduzir o consumo desse bem e elevar a receita do governo. Qual passará
a ser a nova quantidade de equilíbrio? Qual o preço que o comprador
passará a pagar? Qual o valor que o vendedor passará a receber por cada
unidade?
A cobrança de um imposto de $1,00 por unidade desloca a curva de
demanda para a esquerda: para cada preço, o consumidor deseja
comprar menos. Em termos algébricos, a nova função de demanda
é:
P = 9 - Q.
A nova quantidade de equilíbrio pode ser calculada da mesma
forma que no item (2a):
9 - Q = Q - 4, ou Q* = 6,5.
Para determinar o preço pago pelo comprador, PB* , use o valor de
Q* na equação de demanda:
PB* = 10 - 6,5 = $3,50.
Para determinar o preço pago pelo vendedor, PS* , use o valor de Q*
na equação de oferta:
PS* = 6,5 - 4 = $2,50.
c.
Suponha que o governo mude de opinião a respeito da importância desse
bem para a satisfação do público. Dessa forma, o imposto é removido e um
subsídio de $1 por unidade é concedido a seus produtores. Qual será a
nova quantidade de equilíbrio? Qual o preço que o comprador passará a
pagar? Qual o valor que o vendedor passará a receber (incluindo o
subsídio) por cada unidade? Qual será o custo total para o governo?
A curva de oferta original era P = Q - 4. Com um subsídio de $1,00
para os produtores, a curva de oferta se desloca para a direita.
Lembre-se de que a curva de oferta de uma empresa é sua curva de
custo marginal. Com um subsídio, a curva de custo marginal se
desloca para baixo na magnitude do subsídio. A nova função de
oferta é:
P = Q - 5.
Para obter a nova quantidade de equilíbrio, considere a nova curva
de oferta igual à curva de demanda:
Q - 5 = 10 - Q, ou Q = 7,5.
O comprador paga P = $2,50, e o vendedor recebe esse valor mais o
subsídio, isto é, $3,50. Com a quantidade de 7.500 e um subsídio de
$1,00, o custo total do subsídio para o governo será de $7.500.
3. Os produtores japoneses de arroz têm custos de produção extremamente
elevados, em parte devido ao alto custo de oportunidade da terra e à sua
capacidade de tirar proveito da produção em grande escala. Analise as seguintes
políticas destinadas a garantir a preservação da produção de arroz pelos
japoneses: (1) concessão de um subsídio para cada libra de arroz produzido pelos
agricultores, ou (2) criação de um imposto incidindo sobre cada libra de arroz
importado. Mostre em gráficos de oferta e demanda o preço e a quantidade de
equilíbrio, o nível da produção doméstica de arroz, a receita ou despesa
governamental e o peso morto decorrente de cada política. Qual será a política
que o governo japonês provavelmente preferirá? Qual será a política que os
agricultores japoneses provavelmente preferirão?
A Figura 9.3.a mostra os ganhos e perdas gerados por um subsídio
por libra produzida. S é a oferta doméstica, D a demanda
doméstica, PS o preço subsidiado, PB o preço pago pelos
compradores e PEQ o preço de equilíbrio na ausência de subsídio,
supondo que não haja importações. Com a concessão do subsídio, os
compradores demandam Q1. Os agricultores ganham quantias
equivalentes às áreas A e B  que correspondem ao aumento no
excedente do produtor. Os consumidores ganham o equivalente às
áreas C e F  que correspondem ao aumento no excedente do
consumidor. O peso morto é igual à área E. O governo paga um
subsídio igual às áreas A + B + C + F + E.
A Figura 9.3.b mostra os ganhos e perdas gerados por um imposto
de importação por libra do produto. PW é o preço mundial e PEQ é o
preço de equilíbrio. Com o imposto, dado por PEQ - PW, os
compradores demandam QT,, os agricultores ofertam QD, e QT - QD
é a quantidade importada. Os agricultores obtêm um excedente
equivalente à área A. Os consumidores perdem o equivalente às
áreas A, B e C  o que corresponde à redução no excedente do
consumidor. O peso morto é igual às áreas B e C.
Preço
S
PB
A
B
E
PEQ
C
F
PS
D
Q1
QEQ
Quantidade
Figura 9.3.a
Preço
S
PEQ
A
B
C
PW
D
QD
QEQ
QT
Quantidade
Figura 9.3.b
Na ausência de informações adicionais acerca da magnitude do
subsídio e do imposto, bem como das equações de oferta e demanda,
parece razoável supor que o governo japonês preferiria a adoção do
imposto de importação, enquanto que os agricultores japoneses
prefeririam o subsídio.
4. Em 1983, a administração Reagan lançou um novo programa agrícola
baseado no pagamento em espécie (denominado Payment-in-Kind Program).
Para examinar a forma de funcionamento desse programa, vamos considerar o
mercado do trigo.
a.
Suponha que a função de demanda seja QD = 28 - 2P e função de oferta
seja QS = 4 + 4P, onde P é o preço do trigo em dólares por bushel e Q é a
quantidade em bilhões de bushels. Calcule o preço e a quantidade de
equilíbrio para o livre mercado.
Igualando a demanda e a oferta, QD = QS, obtemos
28 - 2P = 4 + 4P, ou P = 4.
Para determinar a quantidade de equilíbrio, usamos o valor de P =
4 na equação de oferta ou na equação de demanda:
QS = 4 + 4(4) = 20
e
QD = 28 - 2(4) = 20.
b.
Agora suponha que o governo queira reduzir a oferta de trigo em 25%, a
partir do equilíbrio de livre mercado, mediante pagamento aos produtores,
para que retirem suas terras da produção. Entretanto, o pagamento será
feito com trigo em vez de dólares; daí decorre o nome do programa. Este
trigo virá da vasta reserva governamental resultante dos programas de
suporte de preços anteriormente praticados. A quantidade de trigo paga
será igual à que poderia ter sido colhida nas terras que foram retiradas de
produção. Os produtores encontram-se livres para vender esse trigo no
mercado. Qual será a quantidade produzida pelos agricultores de agora
em diante? Qual a quantidade indiretamente fornecida ao mercado pelo
governo? Qual será o novo preço de mercado? Qual será o ganhos dos
produtores? Os consumidores estarão ganhando ou perdendo?
Tendo em vista que, no livre mercado, a oferta dos agricultores é de
20 bilhões de bushels, a redução de 25% estabelecida pelo programa
de pagamento em espécie implicaria uma produção de 15 bilhões de
bushels. Para incentivar os agricultores a deixar de cultivar a
terra, o governo deveria dar a eles 5 bilhões de bushels, que eles
venderiam no mercado.
A oferta total de mercado continua sendo de 20 bilhões de bushels;
logo, o preço de mercado não se altera, permanecendo em $4 por
bushel. Os agricultores recebem do programa governamental $20
bilhões, ou seja, ($4)(5 bilhões de bushels), que correspondem a um
ganho líquido, pois eles não incorrem em nenhum custo para
ofertar no mercado o trigo recebido do governo. O programa
governamental não afeta os consumidores no mercado de trigo, pois
eles continuam comprando a mesma quantidade e pagando o
mesmo preço da situação de livre mercado.
c.
Se o governo não tivesse devolvido o trigo aos agricultores, ele precisaria
tê-lo armazenado ou então destruído. Os contribuintes ganham com a
implementação desse programa? Quais são os problemas potenciais
criados pelo programa?
Dado que o governo não precisa manter estoques de trigo, os
contribuintes ganham com o programa. Aparentemente, todos
ganham com o programa; entretanto, esta situação só pode
perdurar enquanto as reservas de trigo do governo não são
exauridas. O programa pressupõe que as terras que deixaram de
ser cultivadas poderão voltar a ser utilizadas na produção de trigo
assim que as reservas governamentais acabarem; entretanto, caso
isso não seja possível, é possível que os consumidores passem a
pagar mais caro pelos produtos à base de trigo no futuro. Cabe
observar, por fim, que os agricultores também são contribuintes;
dado que a produção de trigo envolve custos, o programa lhes
proporciona um lucro inesperado.
5. Cerca de 100 milhões de libras de confeitos são anualmente consumidos nos
EUA, e o seu preço tem sido de cerca $0,50 por libra. Entretanto, como os
produtores desse bem acham que seus rendimentos estão muito baixos,
conseguiram convencer o governo de que uma política de suporte de preços seria
adequada. Em conseqüência, o governo passará a adquirir a quantidade
necessária de confeitos para que o preço seja mantido no nível de $1 por libra.
Mas a equipe econômica do governo está preocupada com o impacto econômico
desse programa, pois não dispões de nenhuma estimativa para as elasticidades
da oferta ou da demanda de confeitos.
a.
Esse programa poderia custar ao governo mais do que $50 milhões por
ano? Sob quais condições? Esse programa poderia custar menos do que
$50 milhões por ano? Sob quais condições? Ilustre sua resposta por meio
de um diagrama.
O custo do programa é dado por (QS-QD)*$1. Se as quantidades
demandadas e ofertadas forem muito sensíveis a mudanças no
preço, é possível que o programa do governo custe mais do que $50
milhões. De fato, nesse caso a mudança no preço causará grandes
variações nas quantidades ofertadas e demandadas, sendo provável
que QS-QD seja maior do que 50 milhões e que, portanto, o governo
pague mais do que 50 milhões de dólares  conforme mostra a
Figura 9.5.a.i. Por outro lado, se a oferta e a demanda forem
relativamente inelásticas em relação ao preço, a mudança no preço
resultará em pequenas variações nas quantidades ofertadas e
demandadas, de modo que (QS-QD) será inferior a $50 milhões,
conforme mostrado na Figura 9.5.a.ii.
P
S
1.00
.50
D
Q
QD
QS
100
Figura 9.5.a.i
P
S
1.00
.50
D
QD
100
QS
Q
Figura 9,5.a.ii
b.
Este programa poderia custar aos consumidores (em termos de perda de
excedente do consumidor) mais do que $50 milhões por ano? Sob quais
condições? Este programa poderia custar aos consumidores menos do que
$50 milhões por ano? Sob quais condições?
resposta por meio de um diagrama.
Novamente, ilustre sua
Se a curva de demanda for perfeitamente inelástica, a perda no
excedente do consumidor será de $50 milhões, igual a ($0,5)(100
milhões de libras), que representa a maior perda possível para os
consumidores. Se a curva de demanda não for perfeitamente
inelástica, a perda no excedente do consumidor será menor que $50
milhões. Na Figura 9.5.b, a perda no excedente do consumidor é
dada pela área A mais a área B, no caso da curva de demanda ser
D, e dada apenas pela área A, no caso da curva de demanda ser D’.
P
D
1.00
A
S
B
.50
D’
Q
100
Figura 9,5.b
6. Uma determinada fibra vegetal é comercializada em um mercado mundial
altamente competitivo e seu preço mundial é de $9 por libra. Quantidades
ilimitadas encontram-se disponíveis para importação por parte dos EUA a esse
preço. Apresentamos a seguir a oferta e a demanda nos EUA para diversos
níveis de preço.
Preço
Oferta nos EUA
(milhões de
libras)
Demanda nos EUA
(milhões de libras)
3
6
2
4
34
28
9
12
15
18
6
8
10
12
22
16
10
4
Responda as seguintes questões relativas ao mercado nos EUA:
a.
Mostre que a curva de demanda é dada por QD=40-2P, e que a curva de
oferta é dada por QS=2/3P.
Para determinar a equação da demanda, é necessário encontrar
uma função linear QD= a + bP tal que a reta que ela representa
passe por dois dentre os pontos apresentados na tabela, tais como
(15,10) e (12,16). A inclinação, b, é igual à variação na quantidade
dividida pela variação no preço:
∆Q 10 − 16
=
= −2 = b.
∆P 15 − 12
Inserindo, na função linear, o valor de b acima e os valores de Q e P
para um dos pontos  por exemplo, (15, 10) , podemos resolver
para a constante, a:
10 = a − 2(15), ou a = 40.
Logo, QD = 40 − 2P.
De forma análoga, podemos calcular a equação de oferta QS= c + dP
que passa por dois pontos da tabela, tais como (6,4) e (3,2). A
inclinação, d, é dada por
Resolvendo para c:
2
Logo, QS =   P.
 3
b.
∆Q 4 − 2 2
=
= ..
∆P 6 − 3 3
2
4 = c +   ( 6), ou c = 0.
 3
Mostre que, na ausência de restrições ao comércio, os EUA importariam
16 milhões de libras da fibra vegetal.
Na ausência de restrições ao comércio, o preço nos EUA seria igual
ao preço mundial de $9,00. A partir da tabela, podemos ver que, ao
preço de $9,00, a oferta doméstica seria de 6 milhões de libras e a
demanda doméstica seria de 22 milhões de libras. As importações
seriam a diferença entre a demanda doméstica e a oferta doméstica:
22 - 6 = 16 milhões de libras.
c.
Se os EUA impusessem um imposto de importação de $9 por libra, qual
seria o preço no mercado doméstico e o nível de importação? Qual seria a
receita governamental advinda do imposto? Qual seria o tamanho do peso
morto?
Com um imposto de $9,00, o preço nos EUA seria de $15 (preço
doméstico de equilíbrio), e não haveria importações. Por não haver
importações, a receita do governo seria zero. O peso morto seria
igual a
(0,5)(16 milhões de libras)($6,00) = $48 milhões,
onde 16 é a diferença entre as quantidades demandada e ofertada
ao preço de $9, ou seja, 22 - 6, e $6 é a diferença entre $15 e $9.
d.
Se, no lugar de um imposto de importação, os EUA estabelecessem uma
quota de importação de 8 milhões de libras, qual seria o preço doméstico
nos EUA? Qual seria o custo dessa quota para os consumidores norteamericanos da fibra vegetal? Qual seria o ganhos dos produtores norteamericanos?
Com uma quota de importação de 8 milhões de libras, o preço
doméstico seria $12. A esse preço, a diferença entre a demanda
doméstica e a oferta doméstica seria de 8 milhões de libras, isto é,
16 milhões de libras menos 8 milhões de libras. Observe que o
preço de equilíbrio também poderia ser encontrado igualando-se a
demanda à soma da oferta mais a quota, isto é:
2
40 − 2P = P + 8.
3
O custo da quota para os consumidores é igual à área A+B+C+D na
Figura 9.6.f, que é
(12 - 9)(16) + (0,5)(12 - 9)(22 - 16) = $57 milhões.
O ganho dos produtores domésticos é igual à área A na Figura
9.6.d, que é
(12 - 9)(6) + (0,5)(8 - 6)(12 - 9) = $21 milhões.
P
S
20
15
12
A
9
D
C
B
D
6
8
10
16
22
40
Q
Figura 9.6.d
7. Um determinado metal é comercializado em um mercado mundial altamente
competitivo e seu preço mundial é de $9 por onça. A este preço, quantidades
ilimitadas encontram-se disponíveis para importação por parte dos EUA. A
oferta desse metal a partir das empresas de mineração norte-americanas pode
ser representada pela equação QS = 2/3P, onde QS é a produção norte-americana
em milhões de onças e P é o preço no mercado doméstico. A demanda desse
metal nos EUA é expressa pela equação QD = 40 - 2P, onde QD é a demanda
doméstica em milhões de onças.
Nos últimos anos, a indústria norte-americana tem sido protegida por um
imposto de importação $9 por onça. Devido à pressão exercida por outros
governos, os EUA estão planejando reduzir para zero esse imposto de
importação. Sob a ameaça dessa mudança, a indústria norte-americana pleiteia
que seja aprovado um acordo de restrição voluntária capaz de limitar as
importações norte-americanas a 8 milhões de onças por ano.
a.
Sob o imposto de importação de $9, qual seria o preço desse metal no
mercado norte-americano?
Com um imposto de $9, o preço do metal importado no mercado
norte-americano seria de $18, igual ao preço mundial de $9 mais o
imposto. Para determinar o preço doméstico de equilíbrio, iguale a
oferta doméstica à demanda doméstica:
2
P = 40 - 2P, ou
3
P = $15.
A quantidade de equilíbrio é obtida inserindo-se o preço de $15
acima na equação de demanda ou de oferta:
QD = 40 − (2)(15) = 10
e
 2
S
Q =   (15) = 10.
3
A quantidade de equilíbrio é igual a 10 milhões de onças. Dado que
o preço doméstico de $15 é menor do que o preço mundial mais o
imposto, $18, não há importações.
b.
Caso os EUA venham a eliminar o imposto de importação e seja aprovado
o acordo de restrição voluntária, qual deverá ser o preço no mercado
doméstico norte-americano?
Sob o acordo de restrição voluntária, a diferença entre a oferta
doméstica e a demanda doméstica estaria limitada a 8 milhões de
onças, isto é QD - QS = 8. Para determinar o preço doméstico do
metal, resolva para P a partir da equação QD - QS = 8:
2
(40 − 2 P) − P = 8 , ou P = $12.
3
Para um preço de $12, QD = 16 e QS = 8; a diferença de 8 milhões de
onças será suprida por importações.
8. Entre as propostas fiscais examinadas pelo Congresso, existe um imposto
adicional sobre bebidas alcóolicas destiladas. Tal imposto não incidiria sobre a
cerveja. A elasticidade-preço da oferta de bebidas alcóolicas destiladas é de 4,0, e
a elasticidade-preço da demanda é de -0,2. A elasticidade cruzada da demanda
da cerveja em relação ao preço das bebidas alcóolicas destiladas é de 0,1.
a.
Se o novo imposto for criado, a maior parte dessa carga fiscal estará
recaindo sobre os produtores ou sobre os consumidores de bebidas
alcóolicas? Por quê?
A Seção 9.6 fornece uma fórmula para o "repasse" do imposto, isto
é, a fração do imposto que recai sobre o consumidor. Essa fração é
ES
, onde
ES − E D
ES é a elasticidade-preço da oferta e ED é a
elasticidade-preço da demanda. Substituindo ES e ED, a fração do
"repasse" é
4
4
=
≈ 0.95.
4 − (−0.2) 4.2
Logo, 95% do imposto é repassado aos consumidores porque a oferta
é relativamente elástica e a demanda é relativamente inelástica.
b.
De que forma o novo imposto afetaria o mercado da cerveja, supondo que
sua oferta seja infinitamente elástica?
Com o aumento de preço das bebidas alcoólicas destiladas (devido
ao grande repasse do imposto), alguns consumidores passarão a
consumir cerveja, deslocando a curva de demanda da cerveja para a
direita. Com uma oferta infinitamente elástica para a cerveja (uma
curva de oferta horizontal), o preço de equilíbrio da cerveja não
mudará.
9. No Exemplo 9.1, calculamos os ganhos e perdas decorrentes do controle de
preços exercido sobre o gás natural e descobrimos a existência de um peso morto
de $1,4 bilhão. Este cálculo baseou-se em um preço de $8 por barril de petróleo.
Se o preço do petróleo fosse de $12 por barril, qual teria sido o preço do gás
natural no livre mercado? Qual o valor do peso morto resultante caso o preço
máximo permitido para o gás natural tivesse sido de $1,00 por mil pés cúbicos?
O Exemplo 9.1 mostra que as seguintes equações fornecem boas
aproximações para as curvas de oferta e de demanda para o gás
natural nos anos 70:
e
QS = 14 + 2PG + 0.25PO
QD = -5PG + 3.75PO,
onde PG é o preço do gás e PO é o preço do petróleo.
Com o preço do petróleo a $12 por barril, essas curvas se tornam,
e
QS = 17 + 2PG
QD = 45 - 5PG.
Considerando a quantidade demandada igual à quantidade
ofertada,
17 + 2PG = 45 - 5PG, ou PG = $4.
A este preço, a quantidade de equilíbrio é de 25 mil pés cúbicos
(Tcf).
Se um teto de $1 fosse imposto, os produtores ofertariam 19 Tcf e os
consumidores demandariam 40 Tcf. O ganho dos consumidores
corresponde à área A - B = 57 - 3,6 = $53,4 bilhões, na figura
abaixo. A perda dos produtores corresponde à área -A - C = -57 - 9 =
$66,0 bilhões. O peso morto é igual à área C + B, que é igual à
$12,6 bilhões.
Preço
6
D
S
5,2
B
4
C
3
A
2
1
Preço = $1,00
10
19
30
40
Quantidade
50
Figura 9.9
10. O Exemplo 9.5 descreve os efeitos da quota do açúcar. Em 1997, as
importações estavam limitadas a 5,5 bilhões de libras, o que elevou o preço no
mercado norte-americano para $0,22 por libra. Suponha que as importações
tivessem aumentado para 6,5 bilhões de libras.
a. Qual teria sido o novo preço no mercado doméstico dos EUA?
Dadas as equações da demanda total de mercado para o açúcar
nos EUA. e da oferta dos produtores dos EUA:
QD = 27,45 - 0,29P
QS = -7,83 + 1,07P.
A diferença entre a quantidade demandada e ofertada, QD-QS, é a
quantidade de açúcar importado que é restringido pela quota. Se
a quota for aumentada de 5,5 bilhões de libras para 6,5 bilhões de
libras, teremos QD - QS = 6,5 e poderemos resolver para P:
(27,45-.29P)-(-7,83+1,07P)=6,5
35,28-1,36P=6,5
P=21,2 centavos por libra.
Para um preço de $ 0,212 por libra, QS = -7,83 + (1,07)(21,2) =
14,85 bilhões de libras e QD = QS + 6,5 = 21,35 bilhões de libras.
b.
Quanto ganhariam os consumidores e quanto perderiam os produtores?
P
94.7
S
22
21.2
12
a
c
f
b
e
d
g
D
14.8 15.71
21.07 21.3
Q
Figura 9.10.b
O ganho do excedente do consumidor é o equivalente à área a+b+c+d na
Figura 9.10.b. A perda dos produtores domésticos é igual à área a.
Em termos numéricos:
a = (22-21,2)(14,8)+(15,71-14,8)(22-21,2)(0,5)=12,2
b = (15,71-14,8)(22-21,2)(0,5)=0,36
c = (22-21,2)(21,07-15,71)=4,3
d = (22-21,2)(21,3-21,07)(0,5)=0,1.
Esses números estão expressos em bilhões de centavos, ou dezenas de
milhares de dólares.
Logo, o excedente do consumidor aumenta em $169,6 milhões, enquanto
o excedente do produtor doméstico diminui em $122 milhões.
c.
Qual seria o efeito sobre o peso morto e sobre os produtores estrangeiros?
Quando a quota é de 5,5 bilhões de libras, o lucro obtido pelos produtores
estrangeiros pode ser representado pela área c+f na Figura 9.10.b (o
preço mundial do açúcar é presumido em $ 0,12 por libra). Quando a
quota aumenta para 6,5 bilhões, o lucro pode ser, então, representado
pela área e+f+g. Sendo assim, a mudança nos lucros para os produtores
estrangeiros é (e+f+g)-(c+f) ou e+g-c. Em termos numéricos:
e=(15,71-14,8)(21,2-12)=8,37
g=(21,3-21,07)(21,2-12)=2,12
c=(21,07-15,71)(22-21,2)=4,29.
Logo, o lucro obtido pelos produtores estrangeiros aumenta em
$62 milhões. O peso morto da quota diminui o equivalente à área
b+e+d+g, que é igual à $109,5 milhões.
11. Reveja o Exemplo 9.5 das quotas de açúcar. Durante meados dos anos 90,
os produtores de açúcar norte-americanos tornaram-se mais eficientes,
causando um deslocamento da curva de oferta doméstica para a direita. Vamos
examinar as implicações desse deslocamento. Suponha que a curva de oferta se
desloque para a direita em 5,5 bilhões de libras, de tal forma que a nova curva
de oferta seja dada por
Qs = -2,33 + 1,07P.
a.
Mostre que, se a curva de demanda permanece a mesma do Exemplo 9.5, a
demanda doméstica se iguala à oferta doméstica ao preço de $0,219 por
libra. Então, o preço doméstico poderia ser mantido em $0,219 sem
importações.
Para um preço P=0,219 centavos por libra,
QD= 27,45-.29(21,9) = 21,1 bilhões de libras, e
QS= -2,33+1,07(21,9) = 21,1 bilhões de libras.
b.
Suponha que, sob pressão dos produtores estrangeiros, o governo norteamericano permita importações de 2,5 bilhões de libras, requerendo que
os produtores domésticos de açúcar reduzam sua produção no mesmo
montante. Desenhe as curvas de oferta e demanda e calcule o benefício
resultante para os consumidores, o custo para os produtores domésticos
e o ganho dos produtores estrangeiros. Há algum peso morto associado a
essa mudança de política?
Se for permitida uma importação de 2,5 bilhões de libras, então, o
preço doméstico cairá até a diferença entre a quantidade ofertada
e a quantidade demandada ser de 2,5 bilhões de libras. À medida
que o preço cair, a quantidade ofertada diminuirá e a quantidade
demandada aumentará, resultando em uma mudança na
quantidade ofertada menor do que 2,5 bilhões. Para calcular o
preço de equilíbrio e a quantidade, neste caso, observe,
novamente, que a quantidade demandada será igual à quantidade
ofertada mais 2,5:
QD = 27,45 − 0,29 P = −2,33 + 1,07 p + 2,5 = QS + 2,5 ⇒
P = $0,20,
QS = 19,1,
QD = 21,6
A Figura 9.11.b.i ilustra esses resultados.
P
94.6
S
21.9
20
12
a
b
c
d
e
D
19.1
21.6
27.45
Q
Figura 9.11.b.i
Na figura 9.11.b.i, o ganho dos consumidores corresponde à área
a+b (38,7 ou $387 milhões), a perda para os produtores é a área b
(1,4 ou $14 milhões), e o ganho dos produtores estrangeiros é o
equivalente à área c (20 ou $200 milhões). Ocorre uma redução no
peso morto porque há um aumento das importações. Ainda
presumindo que o preço mundial seja igual à 12, o peso morto,
associado à manutenção de um preço de 21,9 e excluindo todas as
importações, corresponde à área b+c+d+e (65,3 ou $653 milhões).
Quando as importações são de 2,5 e o preço cai para 20, o peso
morto é reduzido à área d+e (43,84 ou $438,4 milhões).
Se o governo quisesse reduzir a produção doméstica em
exatamente 2,5 bilhões de libras, então, a situação seria um pouco
diferente. A curva de oferta total corresponde à curva de oferta
doméstica até a quantidade de 21,1-2,5=18,6; nesse ponto, a curva
de oferta se torna horizontal, até atingir a quantidade de
18,6+2,5=21,1, quando se torna vertical  pois não existe mais
importação nem a produção doméstica é permitida. Se a
quantidade total ofertada é de 21,6 bilhões de libras, as empresa
domésticas e estrangeiras podem vender sua produção pelo preço
de 21,9. Neste caso, não há mudança no excedente do consumidor,
os produtores perdem a área a, as empresas estrangeiras ganham
a área a+b+c, e o peso morto é reduzido o equivalente à área b+c,
como ilustrado na figura 9.11.b.ii.
P
S’
S
21.9
a
b
19.6
c
12
D
18.6
21.1
Q
Figura 9.11.b.ii
12. As curvas de oferta e demanda domésticas de um tipo especial de feijão, o
hula bean, são as seguintes:
Oferta: P = 50 + Q
Demanda: P = 200 - 2Q
onde P é o preço em centavos por libra e Q é a quantidade em milhões de libras.
O mercado doméstico norte-americano é pequeno quando comparado com o
mercado mundial desse feijão, no qual o preço corrente é de $0,60 por libra
(preço mundial insensível a mudanças no mercado norte-americano).
O
Congresso está estudando um imposto de importação de $0,40 por libra. Calcule
o preço desse feijão no mercado doméstico norte-americano resultante da
implementação do imposto. Calcule também o ganho ou a perda em dólares para
os consumidores e produtores domésticos, e qual seria a arrecadação do governo
mediante esse imposto de importação.
Para analisar a influência do imposto de importação no mercado
doméstico do feijão hula bean, comece resolvendo para um preço e
quantidade domésticos de equilíbrio. Primeiro, iguale a oferta à
demanda para determinar a quantidade de equilíbrio:
50 + Q = 200 - 2Q, ou QEQ = 50.
Logo, a quantidade de equilíbrio é de 50 milhões de libras.
Substituindo, QEQ = 50 na equação de demanda ou na equação de
oferta para determinar o preço, encontramos:
PS = 50 + 50 = 100 e PD = 200 - (2)(50) = 100.
O preço de equilíbrio P é $1. Entretanto, o preço mundial de
mercado é de $0,60. A este preço, a quantidade doméstica ofertada
é de 60 = 50 - QS, ou QS = 10, e, da mesma forma, a demanda
doméstica ao preço mundial, é de 60 = 200 - 2QD, ou QD = 70. A
importação é igual à diferença entre a demanda e a oferta
doméstica, ou 60 milhões de libras. Se o Congresso impusesse um
imposto de importação de $0,40, o preço efetivo dos importados
aumentaria para $1. Ao preço de $1, os produtores domésticos
satisfazem a demanda doméstica e as importações caem para zero.
Como mostrado na Figura 9.12, o excedente do consumidor, antes
da imposição do imposto de importação, é igual à área a+b+c, ou
(0,5)(200 - 60)(70) = 4.900 milhões de centavos ou $49 milhões. Após
a imposição do imposto, o preço aumenta para $1,00 e o excedente
do consumidor diminui para a área a, ou
(0,5)(200 - 100)(50) = $25 milhões, uma perda de $24 milhões. O
excedente do produtor aumentará o equivalente à área b, ou (10060)(10)+(0,5)(100-60)(50-10)=$12 milhões.
Finalmente, devido à produção doméstica ser igual à demanda
doméstica ao preço de $1, nenhum hula bean é importado e o
governo não obtém receita. A diferença entre a perda do excedente
do consumidor e o aumento no excedente do produtor é o peso morto
que, neste caso, é igual à $12 milhões. Veja a Figura 9.12.
P
S
200
a
100
b
c
60
50
D
Q
10
50
70
100
Figura 9.12
13. Atualmente, a contribuição para o seguro social nos EUA é dividida entre
empregados e empregadores. Os empregadores devem recolher 6,2% sobre o
salário que pagam e os empregados, 6,2% dos salários que recebem. Suponha
que as regras mudem e os empregadores passem a pagar o total de 12,4% e os
empregados nada paguem. Os empregados estariam em uma situação melhor?
Se o mercado de mão-de-obra é competitivo, isto é, se empregadores e
empregados tomam o salário como dado, então a transferência do
imposto dos empregados para os empregadores não afetará a quantidade
de trabalho empregado e o salário líquido de impostos obtido pelos
empregados. A quantidade de trabalho de equilíbrio é determinada pelo
imposto total pago por empregados e empregadores, correspondente à
diferença entre o salário pago pelo empregador e o salário recebido pelo
empregado. Desde que o imposto total não mude, a quantidade de
trabalho empregada e o salário pago pelo empregador e recebido pelo
empregado (líquido de impostos) se mantém inalterados. Logo, o bemestar dos empregados não aumentaria nem diminuiria se os
empregadores passassem a pagar o total da contribuição para a
seguridade social.
14. Você sabe que, se um imposto passar a incidir sobre um determinado
produto, a correspondente carga fiscal é compartilhada por produtores e
consumidores. Você também sabe que a demanda de automóveis envolve um
processo de ajuste de estoques. Suponha que um imposto de 20% passe
subitamente a incidir sobre as vendas de automóveis. A proporção da carga fiscal
paga pelos consumidores apresentaria uma elevação, uma redução, ou
permaneceria constante ao longo do tempo? Explique de forma sucinta. Repita
a questão para o caso da incidência de um imposto de $0,50 por galão de
gasolina.
No caso de produtos cuja demanda envolva um processo de ajuste
de estoques, a curva de demanda é mais inelástica no longo prazo
do que no curto prazo, pois os consumidores podem postergar as
compras desses bens no curto prazo. Por exemplo, diante de uma
elevação do preço, os consumidores podem continuar a usar a
antiga versão do produto, que eles já possuem; no longo prazo,
porém, o novo produto deve ser adquirido. Logo, a curva de
demanda de longo prazo é mais inelástica do que a curva de curto
prazo.
Vejamos o que acontece no caso de um imposto de 20% sobe as
vendas de automóveis no curto e no longo prazo. Em primeiro lugar,
o imposto causa um deslocamento da curva de demanda, pois os
consumidores devem pagar um preço mais elevado pelo produto.
Tendo em vista que se trata de um imposto ad valorem, a curva de
demanda não se desloca de forma paralela à curva original, pois o
imposto por unidade é relativamente mais elevado para preços
mais elevados.
A carga fiscal do imposto é transferida dos produtores para os
consumidores à medida que nos movemos do curto prazo (Figura
9.14.a) para o longo prazo (Figura 9.14.b). Nessas figuras, PO é o
preço ao consumidor, PS é o preço ao produtor, e PO - PS é o valor do
imposto. É razoável supor que os consumidores tenham uma curva
de demanda mais inelástica no longo prazo, pois eles são menos
capazes de ajustar sua demanda às variações no preço;
conseqüentemente, eles absorvem uma proporção maior da carga
fiscal. Em ambas as figuras, a curva de oferta é igual no curto e no
longo prazo. Se a curva de oferta for mais elástica no longo prazo,
uma proporção ainda maior da carga fiscal será transferida aos
consumidores.
Curto Prazo
Preço
D
PO
S
D*
PEQ
PS
Q1
Q0
Quantidade
Figura 9.14.a
Longo Prazo
Preço
D
D*
S
PO
PEQ
PS
Q1 Q0
Quantidade
Figura 9.14.b
Diferentemente do que ocorre no mercado de automóveis, a curva
de demanda de gasolina não é caracterizada por um processo de
ajustamento de estoques. A curva de demanda é mais elástica no
longo prazo do que no curto prazo, pois no longo prazo produtos
substitutos da gasolina se tornam disponíveis (por exemplo, gasóleo
ou propano). O efeito do imposto sobre o mercado de gasolina
também está associado a um deslocamento da curva de demanda;
nesse caso, porém, trata-se de um deslocamento paralelo, pois o
imposto é definido em termos de unidades.
Nas Figuras 9.14.c e 9.14.d, a carga fiscal é transferida dos
consumidores para os produtores à medida que nos movemos do
curto para o longo prazo.
A elasticidade da demanda é
relativamente maior no longo prazo (que é o caso mais comum), o
que resulta em menor consumo de gasolina e na transferência de
parte da carga fiscal de volta para os consumidores. Cabe observar
que, nas figuras, foram considerados apenas deslocamentos da
curva de demanda, sob a hipótese de que a carga fiscal recai sobre o
consumidor. Os mesmos resultados poderiam ser obtidos através do
deslocamento da curva de oferta, supondo-se que as empresas
paguem o imposto.
Curto Prazo
Preço
S
PO
PEQ
PS
D* D
Q1 Q0
Figura 9.14.c
Quantidade
Longo Prazo
Preço
S
PO
PEQ
PS
D
D*
Q1 Q0
Quantidade
Figura 9.14.d
15. Em 1998, os norte-americanos fumaram 23,5 bilhões de maços de cigarros,
pagando um preço médio no varejo de $2 por maço.
a.
Dada uma elasticidade da oferta de 0,5 e uma elasticidade da demanda
de -0.4, derive curvas lineares para a demanda e a oferta de cigarros.
Suponha que as curvas de demanda e oferta tenham,
respectivamente, as seguintes formas gerais: Q=a+bP e Q=c+dP,
onde a, b, c, e d são constantes cujo valor deve ser determinado a
partir das informações acima. Em primeiro lugar, lembre da
fórmula da elasticidade-preço da demanda:
P ∆Q
D
EP =
.
Q ∆P
Conhecemos o valor da elasticidade, P e Q, o que significa que
podemos resolver para a inclinação da curva de demanda, b:
− 0,4 =
2 ∆Q
23,5 ∆P
∆Q
 23,5 
= −0,4
 = −4,7 = b
∆P
 2 
Para calcular a constante, a, devemos inserir os valores de Q, P e b
na equação da curva de demanda: 23,5=a-4,7*2, de modo que
a=32,9. A equação da demanda é, portanto, Q=32,9-4,7P. Para
encontrar a curva de oferta, podemos partir da fórmula da
elasticidade da oferta e seguir o mesmo procedimento acima:
P ∆Q
Q ∆P
2 ∆Q
0,5 =
23,5 ∆P
E PS =
∆Q
 23,5 
= 0,5
 = 5,875 = d
∆P
 2 
Para calcular a constante, c, devemos inserir os valores de Q, P e d
na equação da curva de oferta: 23,5=c+5,875*2, de modo que
c=11,75. A equação da oferta é, portanto, Q=11,75+5,875P.
b.
Em Novembro de 1998, após aceitar um acordo judicial numa ação
movida por 46 estados norte-americanos, as três maiores empresas fabricantes
de cigarros aumentaram o preço do maço do cigarro no varejo em $0,45. Quais
são os novos preço e quantidade de equilíbrio? Quantos maços de cigarros a
menos são vendidos?
O novo preço do maço de cigarros é $2,45. Pela curva de demanda
vemos que, para esse preço, a quantidade demandada é de 21,39
bilhões de maços, o que representa uma redução de 2,11 bilhões de
maços. Observe que esse resultado poderia ser obtido através da
fórmula da elasticidade:
%∆Q %∆Q
ε Dp =
=
⇒ %∆Q = 9%.
%∆P 22.5%
A nova quantidade demandada é, então, 23,5*0,91=21,39 bilhões
de maços.
c.
Os cigarros estão sujeitos a um imposto federal, cujo valor em 1998 era
de cerca de $0,25 por maço. O valor desse imposto deverá aumentar em $0,15
em 2002. De que forma deverão mudar o preço e a quantidade de equilíbrio?
O imposto de $0,15 causa um deslocamento da curva de oferta
para cima nesse mesmo valor. Para encontrar a nova curva de
oferta, reescrevamos a equação da curva de oferta como uma
função de Q em vez de P:
QS
11,75
QS = 11,75 + 5,875 P ⇒ P =
−
5,875 5,875
A nova curva de oferta é, então:
QS
11,75
P=
−
+ 0,15 = 0,17QS − 1,85
5,875 5,875
Para encontrar a quantidade de equilíbrio, devemos igualar a
nova equação de oferta à equação de demanda. Primeiro,
precisamos reescrever a demanda como uma função de Q em vez
de P:
QD = 32,9 − 4,7 P ⇒ P = 7 − 0,21Q D
Igualando a oferta e a demanda e resolvendo para a quantidade de
equilíbrio:
0,17Q − 1,85 = 7 − 0,21Q ⇒ Q = 23,12
Inserindo a quantidade de equilíbrio na equação de demanda,
obtemos um preço de equilíbrio de $2,09.
Cabe observar que estamos supondo que os itens (b) e (c) desta
questão sejam independentes. Se a informação do item (b) fosse
usada no item (c), a curva de oferta passaria ser $0,60 (0,45+0,15)
mais alta do que a curva de oferta original.
d.
Que proporção do imposto federal será paga por consumidores e
produtores?
Dado que o preço aumentou em $0,09, os consumidores deverão pagar $0,09 dos
$0,15 de imposto, ou seja, 60% do imposto, e os produtores pagarão os restantes
$0,06, ou 40% do imposto.