20 100 20 500 100 500 500 400 - = - = - =

RESOLUÇÃO DA PROVA DE MATEMÁTICA VESTIBULAR DA UNICAMP 2016 FASE 1.
POR PROFA. MARIA ANTÔNIA CONCEIÇÃO GOUVEIA
QUESTÃO 41
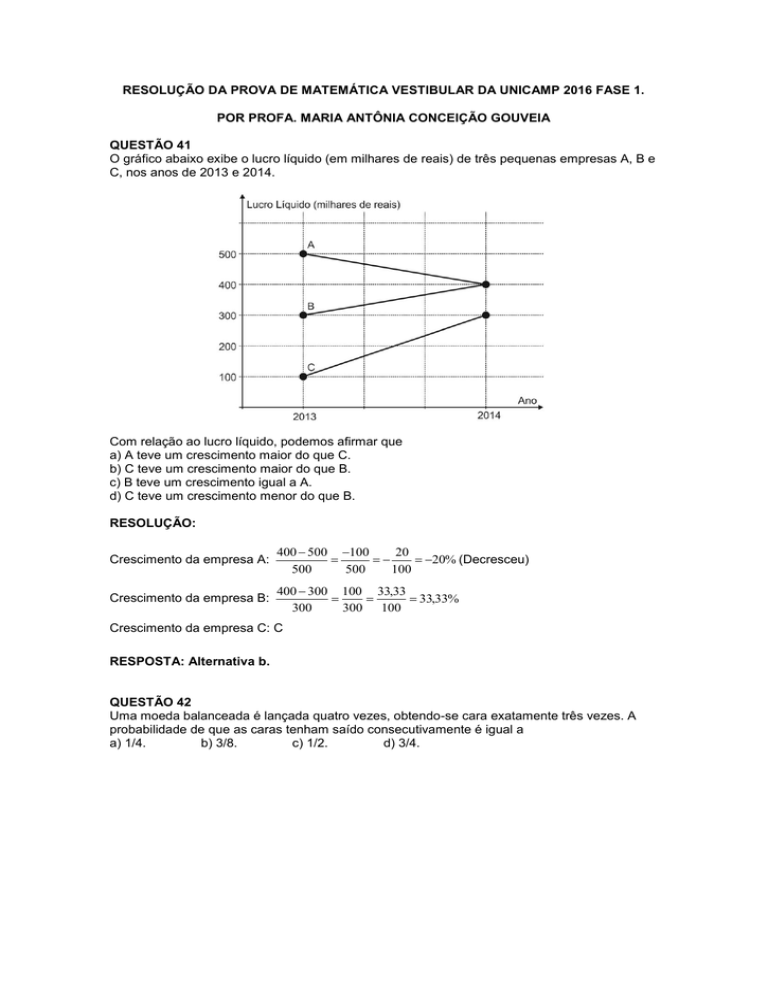
O gráfico abaixo exibe o lucro líquido (em milhares de reais) de três pequenas empresas A, B e
C, nos anos de 2013 e 2014.
Com relação ao lucro líquido, podemos afirmar que
a) A teve um crescimento maior do que C.
b) C teve um crescimento maior do que B.
c) B teve um crescimento igual a A.
d) C teve um crescimento menor do que B.
RESOLUÇÃO:
Crescimento da empresa A:
400  500 100
20


 20% (Decresceu)
500
500
100
Crescimento da empresa B:
400  300 100 33,33


 33,33%
300
300 100
Crescimento da empresa C: C
RESPOSTA: Alternativa b.
QUESTÃO 42
Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A
probabilidade de que as caras tenham saído consecutivamente é igual a
a) 1/4.
b) 3/8.
c) 1/2.
d) 3/4.
RESOLUÇÃO:
Possibilidades de se obter cara exatamente três vezes:
1
2
3
4
C
C
C
Co
C
C
Co
C
C
Co
C
C
Co
C
C
C
São 4 as possibilidades de ocorrência, mas apenas em duas as caras saíram
2 1
consecutivamente. Logo a probabilidade pedida é:  .
4 2
RESPOSTA: Alternativa c.
QUESTÃO 43
Em uma matriz, chamam-se elementos internos aqueles que não pertencem à primeira nem à
última linha ou coluna. O número de elementos internos em uma matriz com 5 linhas e 6
colunas é igual a
a) 12.
b) 15.
c) 16.
d) 20.
RESOLUÇÃO:
 
 a
1

 a5

 a9
 



a2 a3 a4
a6 a7 a8
a10 a11 a12









Uma matriz com 5 linhas e 6 colunas tem 5 × 6 = 30 elementos.
Destes elementos, o número de internos é (6 – 2) × (5 – 2) = 12,
conforme o exemplo ao lado:
RESPOSTA: Alternativa a.
QUESTÃO 44
Considere o gráfico da função y = f (x) exibido na figura a seguir.
-1
O gráfico da função inversa y = f (x) é dado por
a)
b)
c)
d)
RESOLUÇÃO:
-1
Se a função f tem inversa, então os gráficos de y = f(x) e y = f (x) são reflexões um do outro
em relação a reta y = x; isto é, cada um é a imagem especular do outro com relação àquela
reta.
RESPOSTA: Alternativa c.
QUESTÃO 45
Considere a função afim f (x) = ax + b definida para todo número real x , onde a e b são
números reais. Sabendo que f (4) = 2 , podemos afirmar que f ( f (3) + f (5)) é igual a
a) 5.
b) 4.
c) 3.
d) 2.
RESOLUÇÃO:
f (4) = 2  4a + b = 2  b = 2 – 4a 
f (x) = ax + 2 – 4a.
A partir dessa equação de f(x):
 f (3) = 3a + 2 – 4a  f (3) = –a + 2.
 f (5) = 5a + 2 – 4a  f (5) = a + 2.

f(3) + f(5) = –a + 2 + a + 2 = 4  f(f(3) + f(5)) = f(4)


f(4)= 4a + 2 – 4a  f(4) = 2 
f(f(3) + f(5)) = 2.
RESPOSTA: Alternativa d.
QUESTÃO 46
A solução da equação na variável real x, logx ( x + 6) = 2 , é um número
a) primo.
b) par.
c) negativo.
d) irracional.
RESOLUÇÃO:
Domínio da função:
x  0, x  1
x  0, x  1
 
 D(f)  x  0, x  1

x  6  0
x  6
log x (x  6)  2  x  6  x 2  x 2  x  6  0  (x  3)(x  2)  0 
x  3 ou x  2 (não convém)
A solução da equação é x = 3.
RESPOSTA: Alternativa a.
QUESTÃO 47
Seja (a,b,c) uma progressão geométrica de números reais com a ≠ 0 . Definindo s = a + b + c ,
o menor valor possível para s / a é igual a
a) 1/2.
b) 2/3.
c) 3/4.
d) 4/5.
RESOLUÇÃO:
2
Sendo (a,b,c) uma progressão geométrica de números reais com a ≠ 0, b =aq e c = aq .
Então s = a + aq + aq 
2
s a(1  q  q 2 )

 q 2  q  1.
a
a
s
o
 q 2  q  1 ,é uma função do 2 , seu menor valor é aquele
a

 1  4 3

 .
que assume no vértice:
2
4 1
4
4  coeficient e de q
Como
RESPOSTA: Alternativa c.
QUESTÃO 48
 x  y  1,

Considere o sistema linear nas variáveis reais x , y , z e w,  y  z  2,
w  z  3.

Logo, a soma x + y + z + w é igual a
a) 2.
b) 0.
c) 6.
d) 8.
RESOLUÇÃO:
 x  y  1,
 x  y  1,
 y  z  2,


y

z

2
,
(L

L

L
)



1
2
3
w  z  3.
w  z  3,

  
 y  z  2,

 x  y  z  w  ( x  w)  ( y  z )  6  2  8
 x  w  6.
RESPOSTA: Alternativa d.
QUESTÃO 49
 cos x 0  sen x 
Considere a matriz quadrada de ordem 3, A   0
1
0  , onde x é um número real.
sen x 0 cos x 
Podemos afirmar que
a) A não é invertível para nenhum valor de x .
b) A é invertível para um único valor de x .
c) A é invertível para exatamente dois valores de x .
d) A é invertível para todos os valores de x .
RESOLUÇÃO:
Para que A seja invertível é necessário que detA  0.
cos x 0  sen x
det A 
0
1
sen x 0
0  det A  cos2 x  sen 2 x  det A  1
cos x
RESPOSTA: Alternativa d.
QUESTÃO 50
2
2
Considere o círculo de equação cartesiana x + y = ax + by , onde a e b são números reais
não nulos. O número de pontos em que esse círculo intercepta os eixos coordenados é igual a
a) 1.
b) 2.
c) 3.
d) 4.
RESOLUÇÃO:

Fazendo x = 0 em x 2  y 2  ax  by  0 , tem-se
y 2  by  0  y( y  b)  0  y  0 ou y  b .

A circunferência passa pelos pontos (0,0) e (0,b).
Fazendo y = 0 em x 2  y 2  ax  by  0 , tem-se
x 2  ax  0  x( x  a)  0  x  0 ou x  a .
A circunferência passa pelos pontos (0,0) e (a,0).
Conclusão: A circunferência intercepta os eixos coordenados nos pontos (0,0), (a, 0) e (0, b).
RESPOSTA: Alternativa c.
QUESTÃO 51
A figura abaixo exibe um quadrilátero ABCD, onde AB = AD e BC = CD = 2 cm. A área do
quadrilátero ABCD é igual a
a) 2cm 2
b) 2cm2
c) 2 2cm 2
d) 3cm2
RESOLUÇÃO:
Ao triângulo BCD aplicando a lei dos cossenos:
2
x 2  4  4  2.2.2. cos 45  x 2  8  8.
 x2  8  4 2
2
Do triângulo retângulo ABD:
x2  2 y2  2 y2  8  4 2  y 2  4  2 2
SABCD = SABD + SBCD  SABCD =
y2 1
42 2
2
 .2.2.sen45  SABCD =
 2.

2 2
2
2
SABCD = 2  2  2  SABCD = 2 .
RESPOSTA: Alternativa b
QUESTÃO 52
Um cilindro circular reto, cuja altura é igual ao diâmetro da base, está inscrito numa esfera. A
razão entre os volumes da esfera e do cilindro é igual a
a) 4 2 / 3
b) 4 / 3.
c) 3 2 / 4 .
d)
2 .
RESOLUÇÃO:
Sendo o cilindro equilátero, o diâmtro da base e a sua altura são
iguais a 2r. Considerando R a medida do raio da esfera na qual
está inscrito.
O triângulo retângulo AOB, na figura ao lado tem R e r como
medidas, respectivamente, da hipotenusa e dos catetos.
Determinando o valor de R em função de r:
R 2  r 2  r 2  R 2  2r 2  R  r 2 .
O volume do cilindro é: Vcil  r 2  h  r 2  2r  2r 3 .
O volume da esfera é: Vesf
 
4R 3 4 r 2


3
3
3
4r 3  23 
3

  8r 2 .

3
3
A razão entre os volumes da esfera e do cilindro é :
8r 3 2
8r 3 2
1
4 2
 2r 3 


.
3
3
3
3
2r
RESPOSTA: Alternativa a.
QUESTÃO 53
3
2
Considere o polinômio cúbico p(x) = x + x − ax − 3 , onde a é um número real. Sabendo que r
e −r são raízes reais de p(x) , podemos afirmar que p(1) é igual a
a) 3.
b) 1.
c) 2.
d) 4.
RESOLUÇÃO:
Considerando t como a terceira raiz do polinômio e aplicando as relações de Girard:
1
r  (r )  t 
 t  1
1
A terceira raiz é 1.
Substituindo esse valor em p(x): p(1) = 0  1 + 1 + a – 3 = 0  a = 3 
p(x) = x + x − 3x – 3  p(1) = 1 + 1 – 3 – 3 = – 4.
3
2
RESPOSTA: Alternativa d.
QUESTÃO 54
1  ai
, onde a é um número real e i é a unidade imaginária,
a i
2
2016
isto é, 1 = −1. O valor de z
é igual a
2016
a) a
b) 1.
c) 1+ 2016i .
d) i .
Considere o número complexo z 
RESOLUÇÃO:
z


1  ai 1  ai a  i 
a  i  a 2i  a a 2i  i i a 2  1

z
 2
 2
i
a  i a  i 
a i
a i
a 1
a 2  i 2
Sabe-se que: i 0  1; i1  i; i 2  1; i 3  i; i 4  1; i 5  i;.....
A partir de i 4 repete-se a sequência dos resultados: 1; i;  1;  i; 1; i; i;  1;  i; 1; i;.....
Sabe-se que 2016 é um múltiplo de 4, então o resto da divisão de 2016 por 4 é zero e
z 2016  i 2016  i 0  1 .
RESPOSTA: Alternativa b.