Aula 08

Mecânica I (FIS-14)
Prof. Dr. Ronaldo Rodrigues Pelá
Sala 2602A-1
Ramal 5785
[email protected]
www.ief.ita.br/~rrpela
Journal Club
Nature Mat. 12, 779 (2013)
Onde estamos?
●
Nosso roteiro ao longo deste capítulo
–
Cinemática retilínea: movimento contínuo
–
Cinemática retilínea: movimento irregular
–
Movimento curvilíneo geral
–
Movimento curvilíneo: componentes retangulares
–
Movimento de um projétil
–
Movimento curvilíneo: componentes normal e tangencial
–
Movimento curvilíneo: componentes cilíndricas
–
Análise do movimento absoluto dependente de duas partículas
–
Movimento relativo de duas partículas usando eixos de translação
–
Movimento relativo de duas partículas usando eixos de rotação
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Motivação
–
Movimento restringido por meio do controle de
uma distância radial e de uma posição angular
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Motivação
–
Movimento restringido por meio do controle de
uma distância radial e de uma posição angular
Braço robótico para efetuar pintura
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Motivação
–
Movimento restringido por meio do controle de
uma distância radial e de uma posição angular
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Motivação
–
Movimento é observado por medidas de uma
distância radial e de uma posição angular
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Motivação
–
Movimento é observado por medidas de uma
distância radial e de uma posição angular
2.8 – Movimento curvilíneo:
componentes cilíndricas
Às vezes, o movimento da partícula está restrito a uma trajetória que
é mais bem descrita utilizando-se coordenadas cilíndricas. Se o
movimento é restrito ao plano, então coordenadas polares são
usadas.
Coordenadas polares
Podemos especificar a posição da partícula
utilizando uma coordenada radial r, que se
estende para fora a partir da origem fixa O
até a partícula, e a coordenada transversal
θ, que é o ângulo no sentido anti-horário
entre uma linha de referência fixa e o eixo r.
2.8 – Movimento curvilíneo:
componentes cilíndricas
Posição
Em qualquer instante, a posição da partícula é definida pelo vetor
posição:
Velocidade
A variação temporal de ur é, então, ur. Para ângulos θ pequenos
esse vetor tem uma intensidade Δur ≈ 1 (Δθ) e age na direção uθ.
Portanto, Δur = Δθuθ, e assim,
2.8 – Movimento curvilíneo:
componentes cilíndricas
Velocidade
A velocidade pode ser escrita na forma de componentes como:
onde:
2.8 – Movimento curvilíneo:
componentes cilíndricas
Aceleração
2.8 – Movimento curvilíneo:
componentes cilíndricas
Aceleração
Podemos escrever a aceleração na forma de componentes como:
onde:
Visto que ar e aθ são sempre
perpendiculares, a intensidade
da aceleração é simplesmente
o valor positivo de:
2.8 – Movimento curvilíneo:
componentes cilíndricas
Coordenadas cilíndricas
As derivadas temporais deste vetor são
zero, e, portanto, a posição, velocidade
e aceleração da partícula podem ser
escritas em termos das suas coordenadas cilíndricas, como a seguir:
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo: A barra OA gira no plano horizontal de tal maneira que
Ao mesmo tempo, o anel B está escorregando para fora ao
longo de OA de maneira que
Se em ambos os casos t é dado em s, determine a velocidade e
a aceleração quando t = 1,00 s.
2.8 – Movimento curvilíneo:
componentes cilíndricas
Para t = 1,00 s
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo: A rotação do braço com uma ranhura radial é dada por
onde  é dado em radianos e t é dado em segundos. Simultaneamente, o
parafuso no braço movimenta o cursor B e controla sua distância a partir
de O de acordo com
onde r é dado em metros e t é em segundos. Calcule os módulos da
velocidade e da aceleração do cursor para o instante em que t = 3,00 s.
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo:
Para t = 3,00 s
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo: Devido à rotação da barra
bifurcada, a bola desloca-se pela fenda,
descrevendo uma trajetória que em parte
está no formato de uma cardioide,
Onde  é dado em radianos. Se a
velocidade da bola é 1,20 m/s e sua
aceleração é 9,00 m/s2 no instante em que
=180°, determine a velocidade angular e
a aceleração angular da bifurcação.
2.8 – Movimento curvilíneo:
componentes cilíndricas
Para  = 180°:
Como v = 1,20 m/s
Como a = 9,00 m/s2
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
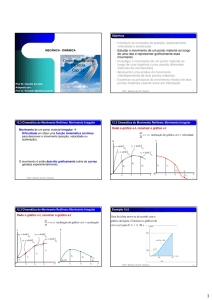
Exemplo: Um radar de rastreamento situase no plano vertical da trajetória de um
foguete que está se deslocando em um
voo sem propulsão acima da atmosfera.
Para o instante mostrado em que  =
30,0°, os dados de rastreamento fornecem
r = 80,0 km, = 1200 m/s e = 0,800°/s. A
aceleração do foguete é devida apenas à
atração gravitacional e para sua altitude
em particular é 9,20 m/s2 verticalmente
para baixo. Para estas condições
determine a velocidade v do foguete e os
valores de e .
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo:
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo: Cada cavalo em um carrossel segue uma trajetória complexa. O poste no qual o cavalo está
preso circula em torno do centro, ao mesmo tempo que o cavalo oscila para cima e para baixo ao longo do
poste. O passeio não é para ser extremamente excitante, de modo que as acelerações precisam ser
limitadas. A sua tarefa é analisar a intensidade da aceleração sentida por uma pessoa montada e construir
um gráfico que indica níveis de aceleração máxima como uma função da distância rh do poste ao centro do
carrossel e da frequência angular  com a qual o carrossel gira. A posição vertical do cavalo é dada por
Suponha que o cavalo oscile com o dobro da frequência do carrossel. z1 = 0,400 m e rh pode variar de 2,44
m a 4,88 m. O tempo que o carrossel leva para completar uma revolução varia entre 3,00 e 5,00 s.
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo:
Dados numéricos
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo:
Maxima
plot3d (w^2*sqrt(r^2+2.56), [w, 1.25, 2.10], [r, 2.44, 4.88])$
2.8 – Movimento curvilíneo:
componentes cilíndricas
●
Exemplo:
Maxima
plot3d (w^2*sqrt(r^2+2.56), [w, 1.25, 2.10], [r, 2.44, 4.88], [mesh_lines_color,
false], [elevation, 0], [azimuth, 0], [colorbox, true], [grid, 150, 150])$