s = s0 +vt - Estruturas.UFPR

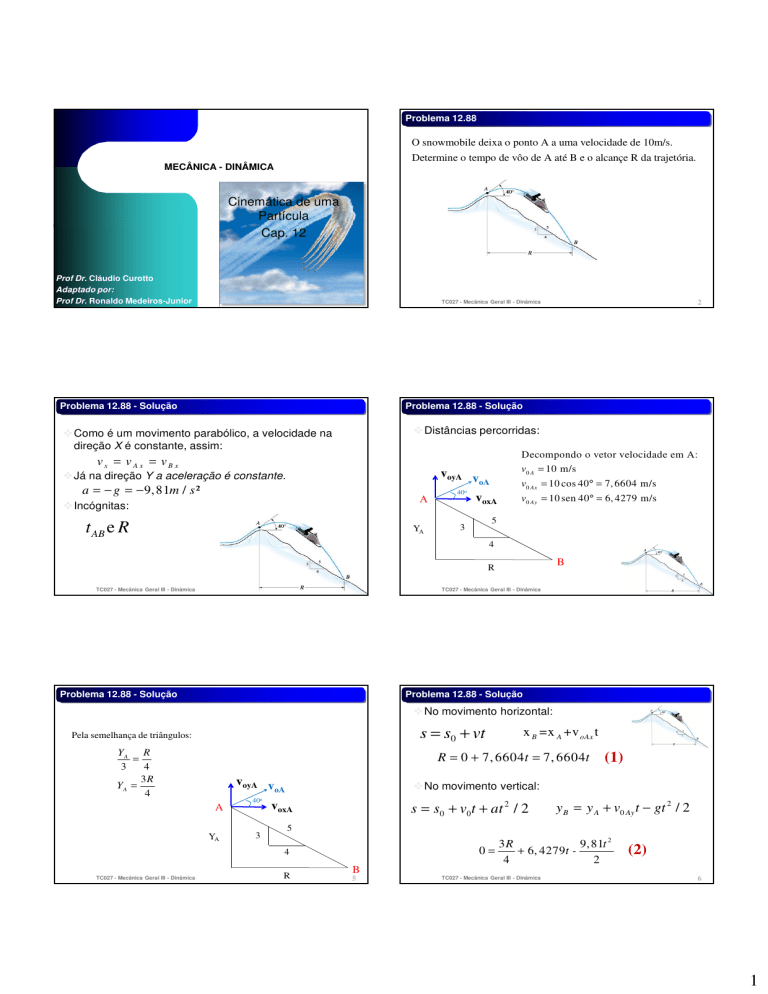
Problema 12.88
O snowmobile deixa o ponto A a uma velocidade de 10m/s.
Determine o tempo de vôo de A até B e o alcançe R da trajetória.
MECÂNICA - DINÂMICA
Cinemática de uma
Partícula
Cap. 12
Prof Dr. Cláudio Curotto
Adaptado por:
Prof Dr. Ronaldo Medeiros-Junior
TC027 - Mecânica Geral III - Dinâmica
Problema 12.88 - Solução
2
Problema 12.88 - Solução
Distâncias percorridas:
Como é um movimento parabólico, a velocidade na
direção X é constante, assim:
vx = vA x = vB x
Decompondo o vetor velocidade em A:
v0 A = 10 m/s
voyA v
oA
Já na direção Y a aceleração é constante.
a = − g = − 9,81m / s ²
A
Incógnitas:
t AB e R
YA
40o
v0 Ax = 10 cos 40° = 7, 6604 m/s
voxA
v0 Ay = 10 sen 40° = 6, 4279 m/s
5
3
4
B
R
TC027 - Mecânica Geral III - Dinâmica
3
Problema 12.88 - Solução
TC027 - Mecânica Geral III - Dinâmica
4
Problema 12.88 - Solução
No movimento horizontal:
s = s0 + vt
Pela semelhança de triângulos:
YA R
=
3
4
3R
YA =
4
R = 0 + 7, 6604 t = 7, 6604t
voyA v
oA
A
YA
40o
3
(1)
No movimento vertical:
s = s0 + v0t + at 2 / 2
voxA
y B = y A + v0 Ay t − gt 2 / 2
5
0=
4
TC027 - Mecânica Geral III - Dinâmica
x B =x A +v oAx t
R
B
5
3R
9, 81t 2
+ 6, 4279t 4
2
TC027 - Mecânica Geral III - Dinâmica
(2)
6
1
Problema 12.88 - Solução
Problema 12.14
Quando o esquiador alcança o ponto A de sua trajetória parabólica, ele
tem uma velocidade escalar de 7 m/s que está aumentando à taxa
constante de 3 m/s2. Determine a direção de sua velocidade e a aceleração
a (módulo, direção e sentido) no instante considerado. Despreze o
tamanho do esquiador.
Substituindo (1) em (2):
3( 7, 6604t)
+ 6, 4279 t - 4, 905t 2 = 0
4
5, 7453t + 6, 4279 t − 4, 905t 2 = 0
y = (1/30)x2
2
− 4, 905t + 12,1732t = 0
Com isso, temos:
t=0
t=
12,1732
∴ t = 2, 4818 s ∴ t = 2, 48 s
4, 9 05
Substituindo em (1):
R = 7, 6604 ( 2, 4818 ) ∴ R = 19 m
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
7
Problema 12.14
8
Problema 12.14
Sistema de coordenadas. A origem A, tomada no esquiador, bem como
as direções e os sentidos dos eixos n e t, estão mostrados na Figura.
Logo, em A, v forma com o eixo x um ângulo ϴ = tg-1(0,667) = 33,7o.
Velocidade: Por definição, a velocidade é sempre tangente à trajetória.
vA = 7 m/s
33,7o
Obs: A derivada da função de y em x é justamente o coeficiente angular
do ponto em questão.
y=
1 2 dy
1
x ∴
=
x
30
dx 15
y = (1/30)x2
y = (1/30)x2
Para x = 10:
dy 10
=
= 0, 667
dx 15
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
9
Problema 12.14
10
Problema 12.14
2
v 
Aceleração: A aceleração é determinada por a = v u t + 
 un
 p 
Raio de curvatura da trajetória em A (10 m, 5 m):
Aceleração:
3/2
1+ ( dy / dx)2 

ρ= 2
2
d y / dx
72 
 un
 26, 04 
 v2 
 un
 p 

a A = 3u t + 
a A = v u t + 
a A = {3 u +1,882u
t
y=
(1/30)x2
n
}m / s2
y = (1/30)x2
Logo:
3/2
  1 2 
1+  x  
  15  
ρ=
1/15
aA =
(3)
2
2
+ (1, 882 ) = 3, 54 m / s 2
Para x = 10:
ρ = 26,04
TC027 - Mecânica Geral III - Dinâmica
11
TC027 - Mecânica Geral III - Dinâmica
12
2
Problema 12.14
Objetivos
Aceleração:
φ = tg − 1 (
φ = tg − 1 (
an
)
at
Ângulo que a aceleração faz
com o eixo tangencial a
trajetória
1, 882
) = 32,1o
3
ϕ
y = (1/30)x2
a A = 3, 54 m / s 2
1,6o
33,7o- 32,1o
= 1,6o
33,7o
a
33,7o
Ângulo que a aceleração faz
com a horizontal
32,1o
TC027 - Mecânica Geral III - Dinâmica
Introduzir os conceitos de posição, deslocamento,
velocidade e aceleração
Estudar o movimento de um ponto material ao longo
de uma reta e representar graficamente esse
movimento
Investigar o movimento de um ponto material ao
longo de uma trajetória curva usando diferentes
sistemas de coordenadas
Apresentar uma análise do movimento
interdependente de dois pontos materiais
Examinar os princípios do movimento relativo de dois
pontos materiais usando eixos em translação
TC027 - Mecânica Geral III - Dinâmica
13
12.8 Movimento Curvilíneo: Componentes Cilíndricos
14
2.5 Vetores Cartesianos
Vetor Unitário:
A direção e o sentido de A pode ser
especificado por um vetor unitário uA
Expressar a posição de um ponto material em
termos de coordenadas cilíndricas: r, ϴ, z.
Coordenadas Polares
Se o problema é restrito ao plano, usam-se as
coordenadas polares r e ϴ.
A
A
⇒ A = Au A
uA =
r coordenada radial, que se estende da origem O ao ponto P.
ϴ coordenada transversal, que é o ângulo medido no sentido
anti-horário, entre uma linha de referência fixa e o eixo r.
u A é um vetor adimensional, que define a direção e o sentido de A
A (escalar positivo) define o módulo de A
TC027 - Mecânica Geral III - Dinâmica
15
12.8 Movimento Curvilíneo: Componentes Cilíndricos
TC027 - Mecânica Geral III - Dinâmica
16
12.8 Movimento Curvilíneo: Componentes Cilíndricos
Velocidade
Coordenadas Polares
vr componente radial, que é uma medida da taxa de aumento ou decréscimo do
comprimento da coordenada radial r.
Vetor de posição: r = r u r
Velocidade: v = r
v=
d ( r ur )
d (r
=
dt
dt
v = r u r + r u r
Como:
u = θ u
)u
e vr = r
θ
r
Então:
v = vr u r + vθ uθ
r
+r
vϴ componente transversal, que é a taxa de variação do movimento ao longo de
uma circunferência de raio r.
d (ur )
dt
dθ
Em particular, o termo θ =
é denominado velocidade angular (rad/s), pois indica
dt
a taxa temporal de variação do ângulo ϴ.
e
vθ = r θ
TC027 - Mecânica Geral III - Dinâmica
Deduções no livro, análogas as
expostas em sala na aula anterior
Obs. A direção de v é a da tangente à
trajetória em P.
17
TC027 - Mecânica Geral III - Dinâmica
18
3
12.8 Movimento Curvilíneo: Componentes Cilíndricos
12.8 Movimento Curvilíneo: Componentes Cilíndricos
Velocidade
Velocidade
RESUMINDO
Escrevendo em função das componentes cartesianas:
v = vr u r + vθ uθ
vr = vr cos θ + vr sen θ
sendo:
v=
2
( vr ) + ( vθ )
2
=
( r )
2
( )
+ r θ
2
vx
TC027 - Mecânica Geral III - Dinâmica
19
TC027 - Mecânica Geral III - Dinâmica
12.8 * Aceleração
12.8 * Aceleração
Derivando v = vr u r + vθ uθ
a = v = ar u r + aθ uθ
Deduzindo
ar = r − r θ 2
aθ = r θ + 2r θ
a=
( ar ) + ( aθ )
2
=
(
r − r θ 2
2
) (
+ r θ + 2r θ
)
20
Derivando v = vr u r + vθ uθ = vr u r + rθuθ
a = v = ar u r + aθ uθ
a = v = vr u r + vr u r + r θuθ + rθuθ + rθu θ
a = ru + r θu + r θu + rθu + rθ −θu
onde
2
vy
vθ = −vr sen θ + vr cos θ
vr = r e vθ = r θ
(
r
2
(
θ
)
)
θ
(
θ
Como:
u r = θ uθ
u = −θ u
θ
r
r
)
a = r − r θ 2 u r + r θ + 2r θ uθ
(
)
2
vθ
r denominado aceleração angular (rad/s ),
pois mede, em cada instante, a taxa temporal de
variação da velocidade angular
TC027 - Mecânica Geral III - Dinâmica
21
12.8 Movimento Curvilíneo: Componentes Cilíndricos
TC027 - Mecânica Geral III - Dinâmica
22
12.8 Movimento Curvilíneo: Componentes Cilíndricos
Coordenadas Cilíndricas
Expressar a posição de um ponto material em
termos de coordenadas cilíndricas: r, ϴ, z.
O vetor uz define a direçã de z;
A posição, velocidade e aceleração podem ser escritas em
termos de suas coordenadas cilíndricas como se segue:
Coordenadas Cilíndricas
Se o problema não é restrito ao plano, usam-se
as coordenadas cilíndricas r, ϴ, z.
r p = ru r + zu z
z coordenada identica a utilizada para as coordenadas cartesianas.
v = r p = ru r +rθuθ + zu z
r coordenada radial, que se estende da origem O ao ponto P.
(
TC027 - Mecânica Geral III - Dinâmica
)
a = v = rp = r − rθ 2 u r + rθ + 2rθ uθ + zu z
ϴ coordenada transversal, que é o ângulo medido no sentido
anti-horário, entre uma linha de referência fixa e o eixo r.
23
(
TC027 - Mecânica Geral III - Dinâmica
)
24
4
Exemplo 12.17
Exemplo 12.17 - Solução
Um brinquedo de um parque de diversões consiste numa cadeira
que gira numa trajetória circular horizontal de raio r presa a um
braço OB que possui velocidade angular θ e aceleração angular
θ. Determine os componentes radiais e transversais da velocidade
vr = r
e aceleração do passageiro. Despreze o tamanho do passageiro.
2
2
ar = r − r θ = − r θ
a = r θ + 2r θ = r θ
Como r = constante: r = 0, logo:
v = 0 e v = r θ
r
θ
θ
TC027 - Mecânica Geral III - Dinâmica
25
TC027 - Mecânica Geral III - Dinâmica
26
5