Cinemática de uma Partícula Cap. 12

Objetivos
Introduzir os conceitos de posição, deslocamento,
velocidade e aceleração
Estudar o movimento de um ponto material ao longo
de uma reta e representar graficamente esse
movimento
Investigar o movimento de um ponto material ao
longo de uma trajetória curva usando diferentes
sistemas de coordenadas
Apresentar uma análise do movimento
interdependente de dois pontos materiais
Examinar os princípios do movimento relativo de dois
pontos materiais usando eixos em translação
MECÂNICA - DINÂMICA
Cinemática de uma
Partícula
Cap. 12
Prof Dr. Cláudio Curotto
Adaptado por:
Prof Dr. Ronaldo Medeiros-Junior
TC027 - Mecânica Geral III - Dinâmica
12.3 Cinemática do Movimento Retilíneo: Movimento Irregular
2
12.3 Cinemática do Movimento Retilíneo: Movimento Irregular
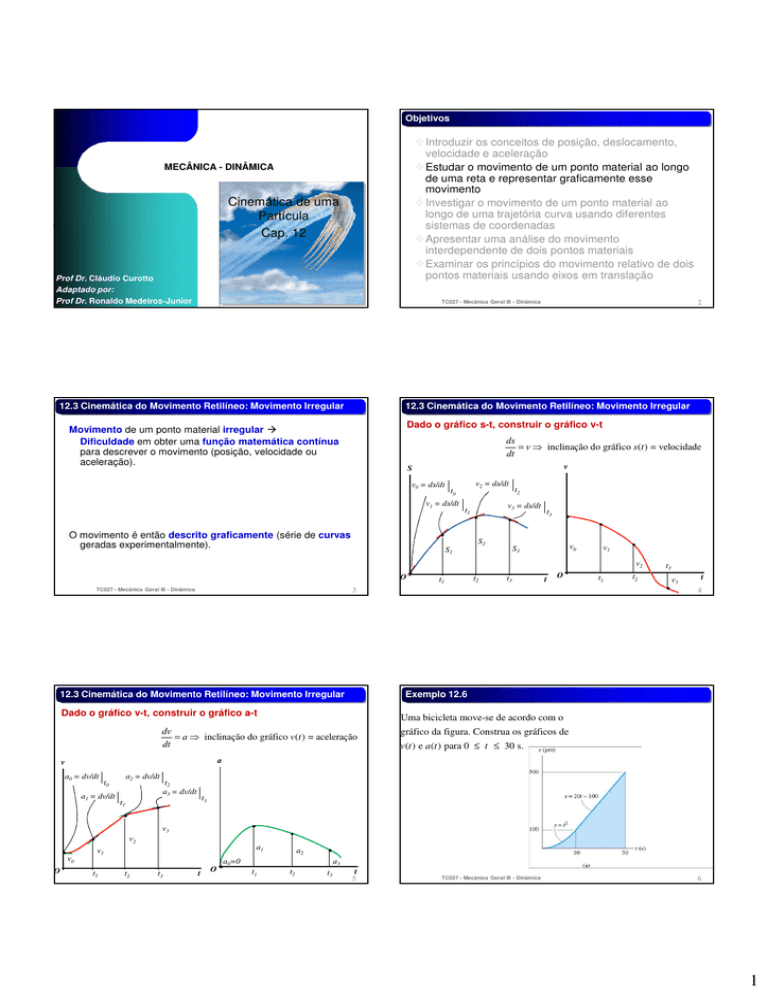
Dado o gráfico s-t, construir o gráfico v-t
Movimento de um ponto material irregular Dificuldade em obter uma função matemática contínua
para descrever o movimento (posição, velocidade ou
aceleração).
ds
= v ⇒ inclinação do gráfico s (t ) = velocidade
dt
v
S
v0 = ds/dt
v2 = ds/dt
t0
v1 = ds/dt
O movimento é então descrito graficamente (série de curvas
geradas experimentalmente).
t2
v3 = ds/dt
t1
S2
t3
v0
S3
S1
v1
v2
O
TC027 - Mecânica Geral III - Dinâmica
3
12.3 Cinemática do Movimento Retilíneo: Movimento Irregular
t1
t2
t3
t
O
TC027 - Mecânica Geral III - Dinâmica
t1
t2
t3
v3
t
4
Exemplo 12.6
Dado o gráfico v-t, construir o gráfico a-t
dv
= a ⇒ inclinação do gráfico v(t ) = aceleração
dt
Uma bicicleta move-se de acordo com o
gráfico da figura. Construa os gráficos de
v(t ) e a (t ) para 0 ≤ t ≤ 30 s.
a
v
a0 = dv/dt
a2 = dv/dt
t0
a1 = dv/dt
t2
a3 = dv/dt
t3
t1
v3
v2
a1
v1
v0
O
a2
a0=0
t1
t2
t
TC027 - Mecânica
Geral 3III - Dinâmica
t
O
a3
t1
t2
t3
t
5
TC027 - Mecânica Geral III - Dinâmica
6
1
Exemplo 12.6 - solução
Problema 12.12
Quando um trem está se deslocando a 2 m/s num trecho retilíneo
0 ≤ t < 10 s: s = t 2 pés
(
)
da estrada, ele começa a acelerar segundo a expressão a = 60v −4 m/s 2 ,
ds
∴ v = 2t pés/s
dt
dv
2
a=
∴ a = 2 pés/s
dt
10 s ≤ t ≤ 30 s: s = 20t − 100 pés
ds
v = ∴ v = 20 pés/s
dt
dv
∴a = 0
a=
dt
v=
onde v é dado em m/s. Determine sua velocidade e posição 3 s após o
início da aceleração.
TC027 - Mecânica Geral III - Dinâmica
7
Exercício 50
TC027 - Mecânica Geral III - Dinâmica
8
Objetivos
Introduzir os conceitos de posição, deslocamento,
velocidade e aceleração
Estudar o movimento de um ponto material ao longo
de uma reta e representar graficamente esse
movimento
Investigar o movimento de um ponto material ao
longo de uma trajetória curva usando diferentes
sistemas de coordenadas
Apresentar uma análise do movimento
interdependente de dois pontos materiais
Examinar os princípios do movimento relativo de dois
pontos materiais usando eixos em translação
Um objeto não identificado percorre uma curva
definida pela equação s = (t3 – 3t2 + 2t) m, onde t está
em segundos. Desenhe os gráficos s-t, v-t, e a-t para
essa partícula no intervalo de tempo 0 ≤ t ≤ 3 s.
TC027 - Mecânica Geral III - Dinâmica
9
12.4 Movimento Curvilíneo Geral (trajetória = curva)
TC027 - Mecânica Geral III - Dinâmica
10
2.2 Operações com Vetores
Adição Vetorial:
Dois vetores adicionados formam o vetor resultante R
⇒ A + B = B + A = R
(comutativo)
r = Vetor de posição
r' = r + ∆s
∆s = r' – r
Velocidade
Lei do paralelogramo
Regra do triângulo
TC027 - Mecânica Geral III - Dinâmica
11
TC027 - Mecânica Geral III - Dinâmica
12
2
2.2 Operações com Vetores
12.4 Movimento Curvilíneo Geral (trajetória = curva)
Adição Vetorial:
Regra do triângulo (extremidade-para-origem)
Conectar a extremidade de A à origem de B. O R resultante se estende da
origem de A à extremidade de B.
r = Vetor de posição
v méd =
TC027 - Mecânica Geral III - Dinâmica
13
12.4 Movimento Curvilíneo Geral (trajetória = curva)
∆r
∆t
r' = r + ∆s
∆s = r' – r
 ∆r 
v = lim∆t →0  
 ∆t 
Velocidade
v=
dr
dt
TC027 - Mecânica Geral III - Dinâmica
14
12.4 Movimento Curvilíneo Geral
Curva gerada pelas extremidades do vetor velocidade
r = Vetor de posição
r' = r + ∆s
∆s = r' – r
Velocidade
Aceleração
v=
dr
dt
∆r aproxima
aproxima--se do comprimento do
arco ∆s no limite de ∆t 0, logo:
v=
ds
dt
Velocidade escalar
a méd =
∆v
∆t
 ∆v 
a = lim∆t →0  
 ∆t 
a=
dv
dt
∆v se aproxima da tangente ao hodógrafo
TC027 - Mecânica Geral III - Dinâmica
15
TC027 - Mecânica Geral III - Dinâmica
16
12.4 Movimento Curvilíneo Geral
Curva gerada pelas extremidades do vetor velocidade
dv
a=
dt
E
dr
v=
dt
d 2r
a= 2
dt
Obs.: v é tangente à trajetória, enquanto a é tangente ao hodógrafo
TC027 - Mecânica Geral III - Dinâmica
17
3