lim ( ) 35 P x =

UNIVERSIDADE FEDERAL DA PARAÍBA
CAMPUS IV-CCAE
CURSO
DISCIPLINA
LICENCIATURA EM MATEMÁTICA
CÁLCULO DIFERENCIAL E INTEGRAL I
José Elias Dos Santos Filho
PROFESSOR
Limite de uma Função
I) Introdução ao Limite de uma Função
Você já deve ter tido a experiência de tentar calcular o custo aproximado de um produto. Imagine
você perguntando a um amigo sobre o custo do quilo do feijão carioquinha nos mercados de sua cidade e
obtém a seguinte resposta: “O custo do feijão carioquinha nos mercados de nossa cidade, eu não sei ao
certo, mas sei que é de aproximadamente R$5,00.”
Veja que se você necessita de 7 quilos de feijão carioquinha, o que teremos é uma estimativa de
quanto você vai gastar para obter os 7 quilos de feijão, isto é, quanto mais próximo de R$5,00 estiver o
custo do feijão, o valor a ser pago pelos 7 quilos estará cada vez mais próximo do valor de R$35,00.
Observe que se “ x ” representa o custo do quilo do feijão carioquinha e “ P ” representa o valor a
ser pago pro 7 quilos de feijão, então
anteriormente, vemos que se
x  5 ), teremos P( x)
x
P( x)  7 x .
Note que, pela situação problema descrito
estiver cada vez mais próximo do valor 5 (denotaremos isso da forma
cada vez mais próximo de 35 (denotaremos isso da forma
P( x)  35 ).
Podemos representar esse fato da seguinte forma:
lim P( x)  35
x5
A notação acima nos diz que se
P( x)  7 x
x
é um valor suficientemente próximo de 5, então o valor da função
estará cada vez mais próximo do valor 35.
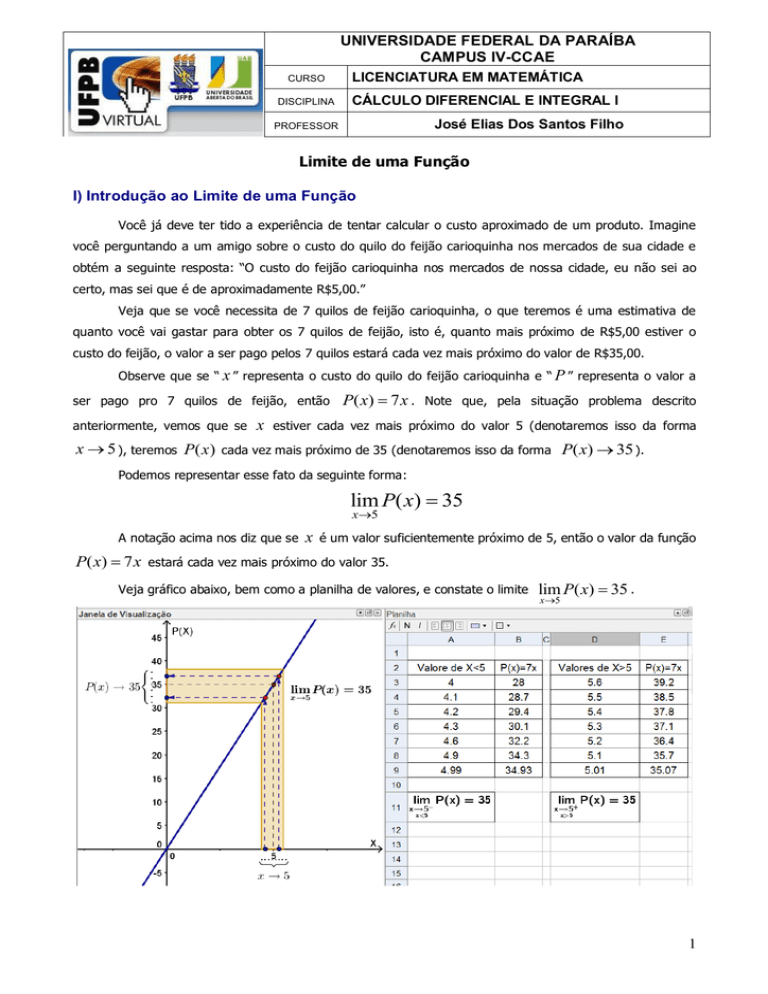
Veja gráfico abaixo, bem como a planilha de valores, e constate o limite
lim P( x)  35 .
x5
1
II) Noção Intuitiva do Limite
O que faremos agora é estudar o que acontece com os valores de uma função
valor de
x
estiver suficientemente próximo de um ponto
dos valores de
a,
xa,
ou seja, se
f ( x)
quando o
qual o comportamento
f ( x) .
Para ficar mais claro o estudo do limite de uma função num ponto, considere a função
x2  1
x2  1
, onde Dom( f )  IR  {1} , ou seja, f ( x) 
f ( x) 
x 1
x 1
Vamos ver o comportamento dos valores de
abaixo com valores de
x2  1
x 1
x
x 1.
tende 1, ou seja,
estarão cada vez mais próximos de 2, isto é,
Desta forma, diremos que o limites de
da forma
quando
x 1.
Para isso, observe a tabela
x  1 (tanto valores x<1 quanto x>1) e os respectivos valores de f ( x) .
Observamos pela tabela acima que se
f ( x) 
f ( x) ,
não esta definida para
f ( x)  2
x2  1
f ( x) 
x 1
quando
x 1
sempre que
x 1
então os valores de
x 1.
é 2 e denotaremos este fato
x2  1
lim f ( x)  lim
 2.
x 1
x 1 x  1
Veja graficamente a ilustração do limite da função
x2  1
f ( x) 
x 1
quando
x 1.
2
Pelo gráfico da função, observe que se o valor de
valor de
f ( x)
x
estiver suficientemente próximo do valor 1, o
estará cada vez mais próximo do valor 2. Assim, diremos que o limite de
tende a 1 é 2 e denotaremos da forma
L
próximos de
L , sempre que x
quando
x
lim f ( x)  2 .
x1
De um modo geral, dizemos que o limite da função
número real
f ( x)
se, e somente se, os números reais
f ( x) , quando x
f ( x) , para
estiver suficientemente próximo de
tende ao valor
os infinitos valores de
x
a,
é igual ao
permanecerem
a.
Notação:
lim f ( x)  L
x a
III) Limites Laterais
Note que quando estudamos o limite da função
considerar valores de
menores que 1 quanto valores de
x
x2  1
quando x  1 , tivemos que
f ( x) 
x 1
x maiores que 1, ou seja, valores x<1 e valores
x>1. Vamos rever novamente a tabela que nos ajudou a determinar o limite
Na tabela na qual temos
Analogamente, na
tabela
lim f ( x)  lim f ( x)  lim
x 1
x 1
x 1
x  1 com x<1, notamos que
x 1
na
qual
x2  1
2.
x 1
temos
x1
x2  1
lim f ( x)  lim f ( x)  lim
 2.
x 1
x 1
x 1 x  1
x 1
x 1
Desta forma, se
lim f ( x)  2 .
com
x 1,
x>1, também
verificamos
que
seja com valores x<1 ou x>1,
x2  1
 2.
x 1 x  1
lim f ( x)  lim
teremos
x 1
O limite
quando
f ( x) 
lim f ( x)  2
x1
x  1 (x<1)
x2  1
x 1
é denominado de limite lateral pela esquerda da função
e o limite
quando
lim f ( x)  2
x1
x2  1
f ( x) 
x 1
é denominado de limite lateral pela direita da função
x  1 (x>1).
3
De uma forma geral, se
simplesmente pela sua direita, e
x
se aproxima de
f ( x)  L
a
através de valores maiores que
a (x  a)
ou
a ( x  a)
ou
escrevemos
lim f ( x)  L . (Esse limite é chamado de limite lateral à direita de a )
x a 
Analogamente, se
se aproxima de
x
f ( x)  M
simplesmente pela sua esquerda, e
a
através de valores menores que
escrevemos
lim f ( x)  M (Esse limite é chamado de limite lateral à esquerda de a )
xa 
Teorema: O limite lim f ( x)  L , se, e somente se, os limites laterais lim f ( x) e lim f ( x )
x a
existirem e forem iguais a
x a
x a
L.
Simplificando:
Note que, para a função
lim f ( x)  L  lim f ( x)  lim f ( x)  L
xa
f ( x) 
xa
x2  1
x 1
temos que
xa
lim
x 1
x2  1
x2  1
 2  lim
x 1 x  1
x 1
e assim
x2  1
lim f ( x)  lim
 2.
x 1
x 1 x  1
Observação Importante:
Se lim f ( x)  lim f ( x) , então não existe lim f ( x) .
xa
x a
xa
Exemplos
1) Calcule o limite
lim g ( x) , caso exista, sabendo que g ( x)  x 2  3x .
x 2
Resolução:
Note que, quando
com x<2) o valor de
x2
x  2 , isto é, x
estará cada vez mais próximo de 4.
Analogamente, quando
esquerda com x<2) o valor de
Assim, quando
mais próximo de
Portanto,
se aproxima de 2, (seja pela direita com x>2 ou pela esquerda
x  2 , isto é, x
3x
se aproxima de 2, (seja pela direita com x>2 ou pela
estará cada vez mais próximo de 6.
x  2 , isto é, x
se aproxima de 2, o valor de
g ( x)  x 2  3x
estará cada vez
4  6  2 , ou seja, g ( x)  x 2  3x  2 , quando x  2 .
lim g ( x)  lim( x 2  3x)  4  6  2 .
x2
x2
Dica para Você: Baixe o arquivo, “Limite g(x).ggb” e veja o gráfico da função
g ( x)  x 2  3x
e do limite
lim g ( x)  2 .
x2
4
2) Considere a função
 x 2  1, se x  1

h( x)   x  3, se 1  x  2
2 x  1, se x  2

Calcule, caso exista, os limites
, cujo gráfico esta representado abaixo.
lim h( x) e lim h( x) .
x1
x2
Resolução:
a) Note que quando consideramos
que quando
x  1 , devemos levar em conta o fato de que x<1 ou x>1. Assim, note
x  1 (x<1), a função é dada por h( x)  x 2  1 .
Logo,
lim h( x)  lim(
x 2  1)  1  1  2

x1
x1
Analogamente, note que quando
Logo,
Como
.
x  1 (x>1), a função é dada por h( x)   x  3 .
lim h( x)  lim(
 x  3)  1  3  2 .

x1
x1
lim h( x)  lim h( x)  2 , então lim h( x)  2 . Observe o gráfico da função e veja este
x1
x1
x1
limite graficamente.
b) Note que quando consideramos
que quando
x  2 , devemos levar em conta o fato de que x<2 ou x>2. Assim, note
x  2 (x<2), a função é dada por h( x)   x  3 .
Logo,
lim h( x)  lim ( x  3)  2  3  1
x2
x2
Analogamente, note que quando
Logo,
Como,
.
x  2 (x>2), a função é dada por h( x)  2 x  1 .
lim h( x)  lim (2 x  1)  4  1  3 .
x2
x2
lim h( x)  lim h( x) , então
x2
x2
o limite
lim h( x)
x 1
não existe.
Observe o gráfico da função e veja que há uma quebra no gráfico da função para valores próximo de
2.
Dica para Você: Baixo o Arquivo “Limite-h(x).ggb” e veja a animação gráfica dessa função.
5
IV) Propriedades do Limite
Suponhamos que lim f ( x)  L , lim g ( x)  M e k  IR .
x a
xa
I) Limite de uma constante
O limite de uma constante é a própria constante, isto é,
Exemplos: a)
lim3  3
b)
x4
lim k  k .
x a
2 2

x8 3
3
lim
II) Limite da soma ( ou da diferença )
O limite da soma (ou da diferença) de duas funções é igual à soma ( ou à diferença ) dos limites
dessas funções, isto é:
lim  f ( x)  g ( x)  lim f ( x)  lim g ( x)  L  M
xa
xa
xa
Exemplos:
a)
lim( x 2  3)  lim x 2  lim3  16  3  19
b)
lim( x  5)  lim x  lim5  2  5  3
x4
x4
x2
x4
x2
x2
II) Limite do produto
O limite do produto de duas funções é igual ao produto dos limites dessas funções, isto é:



lim  f ( x)  g ( x)  lim f ( x)  lim g ( x)  L.M
xa
Exemplo: lim 4 x
x2
2
x a
x a
 lim 4  lim x 2  4  4  16
x2
x2
III) Limite do quociente
O limite do quociente de duas funções é o quociente dos limites dessas funções (exceto quando o
limite do divisor for igual a zero), isto é:
lim
x a
f ( x)
f ( x) lim
L
 x a

g ( x)
lim g ( x) M
, desde que
lim g ( x)  M  0
xa
x a
Exemplo:
x  3) 5
x  3 lim(
 x 2

x 2 x  2
lim( x  2) 4
lim
x 2
IV) Limite de uma potência
O limite de uma potência enésima de uma função é igual à potência enésima do limite dessa função,
isto é:
n
lim[ f ( x)]n  lim f ( x)   Ln
x a
 x a

Exemplo:
2
lim  5 x   lim5 x   102  100
x 2
 x 2 
2
6
V) Limite de uma raiz
O limite da raiz enésima de uma função é igual à raiz enésima do limite dessa função, isto é:
lim n f ( x)  n lim f ( x)  n L , desde que
xa
Exemplo:
n
xa
L
exista.
lim 5 2 x 4  5 lim 2 x 4  5 32  2
x2
x2
-EXERCÍCIOS PROPOSTOS
1) Explique com suas palavras com suas palavras o significado da equação
lim f ( x)  5
x 2
É possível que a equação anterior seja verdadeira, mas que
f (2)  3 ? Explique.
2) Explique o que significa dizer que
lim f ( x)  5
x1
Nesta situação, é possível que
lim f ( x)
x1
e
lim f ( x )  7
x1
exista? Explique.
3) Considere uma função f x  cujo gráfico esta representada abaixo.
Com base no gráfico da função f x  acima, obtenha:
a) lim f  x 
b)lim f  x 
c) lim f  x 
d ) lim f  x 
g ) lim f  x 
h) lim f  x 
i ) lim f  x 
j ) lim f  x 
x 6
x 4
x 2
x 10
x 0
x 10
x 2
e)lim f  x 
x 4
x 6
7
4) Utilize o gráfico da função
limites não existem.
g ( x) para estimar os limites e os valores da função ou explique por que os
a ) lim g ( x)
b) lim g ( x)
c) lim g ( x)
d ) g ( 2)
e) lim g ( x)
f ) lim g ( x)
g ) lim g ( x)
h) g (1)
x 2
x 2
x 2
x 1
x 1
x 1
i ) lim g ( x)
j ) g (2)
x 2
5) Calcule o limite da função no ponto indicado.


a)lim x 2  x  1
x 2

x 2
c)lim x3  3x 2  4 x  2
x5  4 x  3
e)lim
x 0 2 x 3  4 x  2
f )lim x 4  1
x 1

d ) lim x  3 .  x  4 
2
6) Considere as funções
x a
a)lim f ( x) g ( x)
e
g
3
f x 
x  1 g  x 
x0
x a
e

lim g ( x )  2 . Determine:
b)lim 2 f ( x) g ( x)
x a


c) lim
x 2
lim f ( x)  5
f
x 1
b) lim f x .g x 
x 1
8) Os gráficos de
x 3
f x   2 x 2  3x  1 e g x   x 3  2 . Determine :
a) lim  f x   g x 
7) Suponha que

b) lim  3x  4 
c)lim  f ( x)  3g ( x) 
x a
d )lim
x a
f ( x)
f ( x)  g ( x)
são dados. Use-os para calcular cada limite. Caso não exista o limite, explique por
quê.
(a)lim  f ( x)  g ( x)
(b)lim  f ( x)  g ( x) 
(c)lim  f ( x).g ( x) 
 f ( x) 
(d ) lim 

x 1 g ( x)


(e)lim  x3 . f ( x) 
( f )lim  3  f ( x) 
x 1
x 2
x 1
x 2
x 0
8
9) Considere a função
2 x  4 ,

f  x    x  2 ,
 2
 x  4,
a) Calcule o valor da expressão
b) Calcule
se x  2
se  2  x  0 .
se x  0
f (3)  f (2)  f (0)  f (1) ;
lim f x  2.lim f x  lim f x ;
x 2 
x 0 
x 1
c) Represente graficamente essa função.
10) Esboce o gráfico de um exemplo de uma função
f
que satisfaça todas as condições dadas em cada
caso.
a) lim f ( x)  2,
x 1
b) lim g ( x)  1,
x 0
lim g ( x)  0,
x  2
lim f ( x)  2,
x 1
lim g ( x)  1,
x 0 
f (2)  1,
f (1)  2.
lim g ( x)  0,
x  2
f (0) não está definida.
9
UNIVERSIDADE FEDERAL DA PARAÍBA
CAMPUS IV-CCAE
CURSO
LICENCIATURA EM MATEMÁTICA
DISCIPLINA
CÁLCULO DIFERENCIAL E INTEGRAL I
PROFESSOR
José Elias Dos Santos Filho
Limites Infinitos e Limites no Infinito
I-Limites Infinitos
Inicialmente, considere a função
f ( x) 
1
x2
. Note que,
Vamos ver o que acontece com os valores de
f ( x) 
Dom( f )  IR  {0} .
1
x2
, quando
x  0.
Para isso, observe a
tabela abaixo.
Observe que se
f ( x) 
1
x2
x
estiver suficientemente próximo de zero, ou seja, se
cresce indefinidamente, ou seja,
Veja o gráfico da função
f ( x) 
1
x2
f ( x) 
x  0 , então os valores de
1
1
  . Assim, lim f ( x)  lim 2  .
2
x0
x0 x
x
para visualizar o limite
1
 .
x0 x 2
lim f ( x)  lim
x0
1
Veja agora o gráfico da função
g ( x) 
1
, onde Dom( g )  IR  {0} .
x
Observe que se
x  0 , os valores de g ( x) 
x0
Analogamente, observe que quando
g ( x) 
1
x
cresce
lim g ( x)   .
indefinidamente, ou seja,
de
1
x
decresce
x  0 ,
indefinidamente,
os valores
ou
seja,
lim g ( x)   .
x0
Note que não podemos concluir que
nem que
De ponto de vista mais informal, as expressões
que
x0
lim f ( x)  
xa 
respectivamente. Se ambas são verdadeiras, então escrevemos
De forma análoga, as expressões
lim f ( x)  
xa 
decresce indefinidamente, sem cota inferior quando
Se ambas são verdadeiras, então escrevemos
x0
lim g ( x)   .
xa
cresce indefinidamente, sem cota superior quando
f ( x)
lim g ( x)  
xa
e
lim f ( x )  
xa 
significam
pela esquerda ou pela direita,
lim f ( x)   .
xa
e
lim f ( x )  
xa 
significam que
f ( x)
pela esquerda ou pela direita, respectivamente.
lim f ( x)   .
xa
-Dicas Importantes para Você
Considere
n  IN
e
C  IR, com C  0 . Podemos ter assim, os seguintes limites infinitos.
C C
   
n
 x
0
x 0
C C
II ) lim n     se n for PAR.
0
x 0  x
I ) lim
ou
C
C
    se n
lim
n
0
x 0 x
for IMPAR.

Exercícios Resolvidos:
1) Calcule os seguintes limites, caso existam:
a) lim
x 0 
2
x3
b)
lim
x 1
3
x 1
c) lim
x 2
2x  1
x2
d ) lim
x 1
3
x2 1
Resolução:
a) Temos que,
lim
x 0

2
2


3
x3 lim
x 0  x
x0
2
0
  .
Valor Próximo de 0
mas positivo, pois,
x3 0.
2
b) Temos que,
3
3
0

lim
x

1
x 1

  .
x 1 então
x 10
x 2 , então
2 x 15
c) Temos que,
2x  1
5
0

lim
x 2 x  2

  .
x 2 então
x  2 0 
d) Inicialmente note que se
x  1 , então x2  1  0
Assim, devemos calcular os seguintes limites laterais,
x  1 , então x2  1  0 .
e se
3
lim
2
x 1 x  1
e

conclusão sobre o limite
Note que,
3
, antes de tirar alguma
lim
2
x 1 x  1

3
.
lim
2
x 1 x  1
3
3
3
3
    e que lim 2     .
lim
2
x

1
0
0
x 1
x 1 x  1


Portanto, como os limites laterais são diferentes, então
3
lim
2
x 1 x  1
não existe.
-Assíntotas Verticais
Observe o gráfico da função
f ( x) 
8
, onde Dom( f )  IR  {2, 2} .
( x  4)
2
Dica para Você: Baixe o Arquivo “Limite Assíntotas Verticais.ggb” para visualizar o gráfico desta função no
Geogebra.
3
Note que existem duas retas verticais, a saber, a reta
x2
e a reta
x  2 dividem
o gráfico da
função em três partes.
Observe que quando
mais próximo da reta
x  2
x  2
vez mais próximo da reta
x  2
ou
x  2
8
( x  4)
2
estará cada vez
é denominada assíntota vertical da função
f ( x) 
o gráfico da função
x  2 . Desta forma, a reta x  2
8
( x 2  4)
f ( x) .
estará cada
também é denominada assíntota vertical da
f ( x) .
lim f ( x)  
De uma forma geral, quando temos
x a 
ou
xa
Assíntoa
Vertical
f ( x)
f ( x) 
o gráfico da função
x  2 . Desta forma, a reta x  2
Analogamente, quando
função
ou
possui uma assíntota vertical que é a reta
lim f ( x)   ,
x a 
então a função
xa
Assíntoa
Vertical
x  a.
-Exercícios Propostos:
1) Considere o gráfico da função
representado abaixo.
f ( x)
Com base no gráfico da função
f ( x)
ao lado
obtenha:
a) lim f ( x)
b) lim f ( x)
c) lim f ( x)
d ) lim f ( x)
e) lim f ( x)
f ) lim f ( x)
x 2
x 2
x 1
x 1
x 3
x 3
g ) as assíntotas verticais da função. Justifique
cada uma delas.
2) Calcule os seguintes limites, caso existam:
a) lim
x 0
2  3x
x3
b) lim
x 1
1  2x
 x  1
c) lim
2
x 2 
2x  1
x2
d ) lim
x3
4
x 9
2
3) Utilize o software Geogebra para esboçar os gráficos das funções abaixo. Que assíntotas verticais os
gráficos possuem? Por que as assíntotas verticais estão localizadas onde estão?
x2  4
( a ) f ( x) 
x 1
3
(b) g ( x)  x 
x
3
x3  x 2  1
(c)h( x) 
x2  1
(d )k ( x)  2sen( x) 
1
x
4
II- Limites no Infinito
Considere a função
f ( x) 
os valores de
1
,
x
f ( x) 
1
, onde Dom( f )  IR  {0} . Vejamos agora, o
x
quando os valores da variável
x
crescem indefinidamente, ou seja, quando
x   , como também, iremos verificar o que acontece com os valores de f ( x) 
da variável
x
decrescem indefinidamente, ou seja, quando
x   ,
os valores da função
1
 0.
x x
lim f ( x)  lim
x
quando
x   ,
f ( x) 
1
x
f ( x) 
1
x
x
cresce indefinidamente, ou
estão cada vez mais próximos de zero, isto é,
Analogamente, quando os valores de
os valores da função
1
, quando os valores
x
x   . Para isso, observe a tabela abaixo:
Com base na tabela acima, observamos que quando os valores de
seja, quando
que acontece com
x
decresce indefinidamente, ou seja,
estão cada vez mais próximos de zero, isto é,
1
 0.
x x
lim f ( x)  lim
x
De um ponto de vista mais informal, se os valores de uma função
próximos de um número
L
à medida que
lim f ( x)  L , ou seja, f ( x)  L
x
x
x
quando
x   .
f ( x)
ficam cada vez mais próximos de um número
L
decresce sem parar, então escrevemos:
lim f ( x)  L , ou seja, f ( x)  L
x
ficam cada vez mais
cresce sem parar, então escrevemos:
Analogamente, se os valores de uma função
à medida que
f ( x)
quando
x   .
Abaixo veremos uma ilustração gráfica dos limites no infinito.
5
- Dicas Importantes para você
Se
I ) lim
x 
C  IR
C

xn
é uma constante qualquer então:
C

0
II ) lim
x 
Isso significa que x
crece ou decresce
indefinidamente
C

xn
C

0
Isso significa que x
crece ou decresce
indefinidamente
-Exercícios Resolvidos
1) Calcule os seguintes limites:
a) lim
4
3
x   x  1
b) lim
x   x  2 x
2


c) lim x 2  2 x  1
x  
Resolução:
(a) Temos que, note que se
(b) Temos que,
(c) Observe que
3
x  
então
x2  2 x       . Assim,
4
4

0.
lim
2

x  x  2 x
3

 0.
lim

x  x  1
x2  2 x  1  
quando
x   . Assim,
x
lim
x 
2

 2 x  1   .
Abaixo você terá uma ilustração do gráfico de cada uma dessas funções.
6
- Dica Importante para Você:
Limites de polinômios quando x  
O comportamento de um polinômio qualquer
com
P( x)  an xn  an1x n1 
 a2 x 2  a1x  a0 ,
an  0 , coincide com o comportamento final de seu termo de maior grau an x n .
Resumindo, se
P( x)  an xn  an1x n1 
lim (an x n  an1x n1 
x
 a2 x 2  a1x  a0 , com an  0 , então
 a2 x 2  a1x  a0 )  lim an x n
x
e
lim (an x n  an1x n1 
x
 a2 x 2  a1x  a0 )  lim an x n
x
-Exercícios Resolvidos
1)Calcule os seguintes limites, caso existam.
3x  5
x 6 x  8
4 x2  x
x 2 x3  5
(a) lim
(b) lim
5 x3  2 x 2  1
x
1  3x
(c) lim
(d ) lim
3
x
3x  5
6x  8
Resolução:
(a) Pela dica acima, temos que
Assim,
lim (3x  5)  lim 3x
x
x
e que
lim (6 x  8)  lim 6 x .
x
x
3x  5
3x
3 3
 lim
 lim  .
x 6 x  8
x  6 x
x  6
6
lim
(b) Temos que,
4 x2  x
4x2
4
4

lim
 lim

0.
3
3
x  2 x  5
x  2 x
x 2 x

(c) Temos que,
5 x3  2 x 2  1
5 x3
5 x 2 
 lim
 lim

  .
x 
x  3 x
x  3
1  3x
3
(d) Temos que,
lim
lim
lim
x 
3
3x  5 3
3x  5
 lim

x 6 x  8
6x  8
3
3x

x 6 x
lim
3
3 33 31


x 6
6
2
lim
.
7
-Assíntotas Horizontais
Sabemos que função
f ( x) 
8
,
( x  4)
x2
assíntotas verticais, que são as retas
Dom( f )  IR  {2, 2} ,
2
onde
e a reta
x  2 . Um dos argumentos para afirmar que a reta
lim f ( x)   , e
x  2é
uma assíntota vertical da função é o fato de que
x  2
é uma assíntota vertical da função é pelo fato de que
Observe o gráfico da função
função quando
de que
8
( x  4)
2
para afirmarmos que a reta
lim f ( x)   .
x2
e verifique que a reta
y0
limita o gráfico da
x   , ou quando x   . Essa limitação é devido ao fato de que lim f ( x)  0
x
e
lim f ( x)  0 .
x
Assim, diremos que a reta
lim f ( x) 
x 
f ( x) 
x2
apresenta duas
0
y 0
Assíntota
Horizontal
então a função
f ( x)
y0
é uma assíntota horizontal da função
. De uma forma geral, quando temos
lim f ( x) 
x 
possui uma assíntota horizontal que é a reta
L
yL
Assíntota
Horizontal
f ( x) 
ou
8
,
( x  4)
2
lim f ( x) 
x 
pois
,
L
yL
Assíntota
Horizontal
y  L.
8
-Exercícios Resolvidos:
f ( x) 
1) Considere a função
2 x2  4 x  4
. Determinar se a função possui assíntotas horizontais.
x2  2 x
Resolução:
Para verificarmos se a função possui assíntotas horizontais é necessário calcularmos os limites
lim f ( x)
x
e
lim f ( x ) .
x
Assim,
(I)
(II)
2 x2  4 x  4
2 x2
lim f ( x)  lim
 lim 2  lim 2  2 .
x 
x 
x  x
x 
x2  2 x
2 x2  4 x  4
2 x2

lim
 lim 2  2 .
x 
x  x 2
x 
x2  2 x
lim f ( x)  lim
x 
Pelos resultados acima, verificamos que a função
assíntota horizontal que é a reta
Note que a função
x  2
e
x  0.
y  2.
f ( x) 
2 x2  4 x  4
f ( x) 
x2  2 x
possui apenas uma
Veja o gráfico da função abaixo e constate esse fato.
2 x2  4 x  4
x2  2 x
também possui assíntotas verticais que são as retas
x2  2 x
Observe que x=2 e x=0 são as raízes da equação
. Mostre que
Denominador
lim f ( x)   ,
x2
lim f ( x)   , lim f ( x)  
x2
provando que as retas
x  2
x0
e
x0
e
lim f ( x )  
x0
e assim você estará
são as assíntotas verticais da função.
9
- Exercícios Propostos
4) Determine o limite de cada uma das funções quando (a)
2x  3
a ) f ( x) 
5x  7
3x 2  6 x
e) f ( x ) 
4x  8
x 1
b) f ( x )  2
x 3
2 x5  3
f ) f ( x)  2
x  x
x  
e (b)
x   .
1  12 x3
7 x3
c) f ( x)  2
d ) f ( x)  3
4 x  12
x  3x 2  6 x
2 x3  2 x  3
g ) f ( x)  3
3x  3x 2  5 x
5) Para cada uma das funções do exercício (4), determinar as assíntotas horizontais da função.
6) Com base no gráfico da função
g ( x)  2 
sen( x)
x
abaixo, determinar as assíntotas horizontais da
função justificando cada uma delas.
7) Esboce o gráfico de uma função
y  f ( x)
que satisfaça as condições dadas. Nenhuma fórmula é
necessária, simplesmente indique os eixos cartesianos e trace uma curva apropriada.
(a) f (0)  0, f (1)  2, f (1)  2, lim f ( x)  1 e lim f ( x)  1.
x 
x 
(b) f (0)  0, lim f ( x)  0, lim f ( x)  lim f ( x)  , lim f ( x)   e lim f ( x)  .
x 
x 1
x 1
x 1
x 1
8) Utilize o software Geogebra para esboçar os gráficos das funções abaixo. Em cada caso, determine o que
se pede com base no gráfico da função.
( a ) f ( x) 
sen x
;
x
Calcule, caso exista,
1
(b) g ( x)  sen   ;
 x
lim f ( x)
x0
Calcule, caso exista,
(c )
No mesmo plano cartesiano represente
que
f ( x)  h( x)  g ( x)
e
lim g ( x)
x0
lim f ( x ) .
x
.
f ( x)  x , g ( x)   x e h( x)  x .sen( 1x ) .
e com isso estime o valor do limite
(c) Represente graficamente a função
2 x2
g ( x) 
.
3x  6
Verifique
lim h( x) .
x0
A reta x=-2 é uma assíntota vertical da função?
Essa função possui assíntota horizontal? Com base no gráfico, é possível afirmar que a função possui uma
reta com inclinação positiva que representa uma assíntota da função de forma inclinada?
10
UNIVERSIDADE FEDERAL DA PARAÍBA
CAMPUS IV-CCAE
LICENCIATURA EM MATEMÁTICA
CURSO
CÁLCULO DIFERENCIAL E INTEGRAL I
DISCIPLINA
José Elias Dos Santos Filho
PROFESSOR
Limites Indeterminados
-Introdução
f ( x)  x 2  4
Sabemos que para calcular o limite da função
quando
g ( x)  x 2  x  2
e da função
x  2 , procedemos da seguinte forma:
lim f ( x)  lim( x 2  4)  4  4  0
x2
x2
lim g ( x)  lim( x 2  x  2)  4  2  2  0
x2
x2
Isto significa que os valores de
próximo de 0(zero) sempre que
Lembre-se
que
x
f ( x) ,
bem como os valores de
g ( x) ,
estarão suficientemente
estiver suficientemente próximo de 2.
f ( x)  0 e g ( x)  0 ,
pois
x2.
Na
verdade,
o
que
teremos
é
x2
f ( x)  0 e g ( x)  0
sempre que
x  2.
Vejamos agora tentar, de forma direta, calcular o limite da função
f ( x)
x2  4
 2
g ( x) x  x  2
quando
x  2 , vejamos:
lim
x 2
f ( x)
x2  4
44
0
 lim 2

 .
g ( x ) x 2 x  x  2 4  2  2 0
Veja que temos uma expressão da forma
lim
x 2
f ( x) 0
 ,
g ( x) 0
o que significa que tanto o numerador
quanto o denominador, são valores suficientemente próximos de 0(zero) e assim não temos como saber o
comportamento da divisão
0
.
0
Esse limite
lim
x 2
f ( x) 0

g ( x) 0
é denominado de limite indeterminado.
Observe a tabela abaixo e veja o que acontece com os valores de
f ( x)
g ( x)
quando
x  2.
1
Pela tabela acima, vemos que
f ( x)  x2  4  ( x  2)( x  2)
e que
Logo, podemos calcular o limite
lim
x 2
lim
x 2
f ( x)
 0,5 .
g ( x)
De uma forma
mais analítica, note que,
g ( x)  ( x  1)( x  2) .
lim
x 2
f ( x)
g ( x)
da seguinte forma:
( x  2) ( x  2)
f ( x)
( x  2) 4
 lim
 lim
  0,5 .
g ( x) x2 ( x  6) ( x  2) x2 ( x  6) 8
-Limites Indeterminados 0 .
0
Estamos entrando em outra etapa sobre limites, este é conhecido por LIMITES INDETERMINADOS,
sempre que tivermos uma indeterminação do tipo:
0

,
,  -  , 0   , 00 ,  0 , 1
0

Teremos que fazer uso dos nossos conhecimentos algébricos, onde os mais conhecidos são:
Fatoração de Polinômios, Divisão de Polinômios e Multiplicação pelo Conjugado.
Faremos aqui alguns exercícios sobre limites indeterminados. Ante de iniciarmos faremos duas
discussões, uma sobre DIVISÃO ENTRE POLINÔMIOS e outra sobre MULTIPLICAÇÃO OELO CONJUGADO.
-EXERCÍCIOS RESOLVIDOS
1) Seja
f ( x)  x 2  x . O valor do lim
h0
Resolução:
Temos que,
I)
f ( a  h)  ( a  h) 2  ( a  h) 
 a 2  2ah  h2  a  h
II)
f (a)  a 2  a
f ( a  h)  f ( a )
h
é:
Foi feito o seguinte passo aqui: Onde tinha (x) eu
troquei por (a + h), pois estou analisando f(a + h)
Foi feito o seguinte passo aqui: Onde tinha (x) eu
troquei por (a), pois estou analisando f(a)
Agora, substituímos os valores de

f ( a  h)
e
f (a) , para calcular o limite, observe:
 

a 2  2ah  h 2  a  h  a 2  a
f ( a  h)  f ( a )
lim
 lim

h 0
h 0
h
h
a 2  2ah  h 2  a  h a 2 a
2ah  h 2  h
 lim
 lim

h 0
h 0
h
h
 2a h h 2 h 
 lim 

   lim(2a  h  1)  2a  1.
h 0
h
h
h  h 0

f ( a  h)  f ( a )
 2a  1.
Portanto, lim
h0
h
2
2) Calcule o limite
Resolução:
x 2  3x  2
.
x 2
x3  8
lim
Poderemos usar para sair da indeterminação
por usar Fatoração de Polinômios.
0
, a Divisão entre Polinômios ou Fatoração. Neste caso, vamos optar
0
Sabemos pelos produtos notáveis que
I) x2 – a2 = (x – a)(x + a)
II) x3 – a3 = (x – a)(x2 + ax + a2)
Sabendo que
x3  8  x3  23 , e por (II) temos que x3  8  ( x  2)( x 2  2 x  4) .
Com relação ao numerador da fração
são
x1  2 ou x2  1.
x 2  3x  2
2
, vamos determinar as raízes da equação x  3x  2  0 , que
3
x 8
ax2  bx  c  a( x  x1 )( x  x2 )
Como,
então
x2  3x  2  ( x  2)( x  1) .
Assim,
( x  2) .( x  1)
x 2  3x  2
( x  1)
(2  1)
1
lim

lim

lim


.
x 2
x2 ( x  2) .( x 2  2 x  4)
x2 ( x 2  2 x  4)
x3  8
(22  2.2  4) 12
3) Calcule o limite indeterminado
Resolução:
Como as raízes da equação
x2  5x  4
x 4
x4
lim
.
x2  5x  4  0 , são os valores x1  4 ou x2  1, então
x2  5x  4  ( x  4).( x  1).
Desta forma teremos:
( x  4) .( x  1)
x2  5x  4
 lim
¨ lim( x  1)  4  1  3.
x 4
x 4
x 4
x4
( x  4)
lim
Portanto,
x2  5x  4
lim
 3.
x 4
x4
3
MULTIPLICAÇÃO PELO CONJUGADO
Suponha que queremos calcular o limite indeterminado
lim
x 0
x 1  1 x
x
.
Em muitos casos como estes, é de grande importância que nos livremos do termo que envolve a
radiciação e que neste caso é
( x 1 
( x  1  1  x ) . O conjugado do termo ( x  1  1  x )
é o termo
1 x).
Sinal
oposto
ao
anterior
x 1  1 x
x
O que fazemos na prática para calcular o limite, é a multiplicar a fração
fração


pela
 que representa o valor 1.
1 x 
x 1  1 x
x 1 
Assim teremos o seguinte cálculo:
x 1  1 x
lim
 lim
x0
x0
x

x 1  1 x
x
.

,
1 x 
x 1  1 x
x 1 
A intenção de se fazer isso, é produzir a “Diferença de Dois Quadrado”, veja:
( a b )

lim
x 1  1 x
x0
a2
( a b )
x
.

  lim 
1 x 
x 1  1 x
x 1 
b2
 
2
x 1 
x 0
1 x

x
2
.
Efetuando as operações devidas iremos obter o resultado do limite, veja a resolução completa
abaixo:
( a b )
lim
x 0
x 1  1 x
 lim
x 0
x
a2

 lim
x 0

x 1  1 x
x
( a b )
.


1 x 
x 1  1 x
x 1 
b2
 
2
x 1 
x
1 x

2
( x  1)  (1  x)

x 0 x.( x  1  1  x )
 lim
x 1 1  x
2x
 lim

x 0 x.( x  1  1  x )
x 0 x .( x  1  1  x )
2
2
2
 lim

 1
x 0 ( x  1  1  x )
1 1 2
 lim
4
EXERCÍCIOS RESOLVIDOS
1) Determine o valor numérico do limite
lim
x 1
Resolução:
x 1
.
x 1
0
.
0
( x  1)
Observe que se trata de um limite indeterminado
Usaremos a multiplicação pelo Conjugado de
Observe:
que é
 
( x  1) .
2
x  12
x 1
( x  1) ( x  1)
lim
 lim
.
 lim

x 1 x  1
x 1 ( x  1) ( x  1)
x 1 ( x  1).( x  1)
 lim
x 1
( x  1)
( x  1) .( x  1)
Portanto,
lim
x 1 1
 .
x 1 2
lim
y2
.
y 2
x 1
2) Calcule
y 2
1
1
1

 .
x 1 ( x  1)
1 1 2
 lim
Resolução:
Vamos multiplicar a fração
y2
y 2
pelo termo
y 2
, observe os cálculos feitos:
y 2
 y  2   lim ( y  2)  y  2  
 y  2  y  2
 y    2
( y  2)  y  2 
 lim
 lim  y  2   2  2  2
( y  2)
lim
( y  2)
y 2
y 2
Portanto,
.
y 2
y 2
lim
y 2
2
2
2.
y2
 2 2.
y 2
5
-Limites Indeterminados    .
Considere a função
Logo,
teremos
f ( x)  x 4  x 2 .
lim f ( x)  lim ( x 4  x 2 )     ,
x
x
x4  
e
resultado da subtração
x2   ,
.
que é uma indeterminação, pois quando
x  
ou seja, crescem indefinidamente e assim, não podemos estimar o
Para resolver esse tipo de indeterminação, usaremos o fato de que o comportamento de um
P( x)  an xn  an1x n1 
polinômio qualquer
comportamento
seja,
final
de
lim (an x n  an1x n1 
seu
 a2 x 2  a1x  a0 ,
termo
de
maior
 a2 x 2  a1x  a0 )  lim an x n
x
lim f ( x)  lim ( x 4  x 2 )
x
an  0 ,
coincide com o
an x n ,
grau
ou
.
x
Assim, vamos calcular o limite
com
x
da seguinte forma:
lim f ( x)  lim ( x 4  x 2 )  lim x 4   .
x
x
x
- Exercícios Resolvidos
1) Calcule o seguinte limite
3
.
x  2 x  4 x  5
lim
4
Resolução:
Observe que pelo cálculo direto do limite teremos,
3
3

x  2 x  4 x  5
  
lim
.
4
Indeterminação
Vamos usar o fato de que quando
comportamento de
Assim,
o polinômio
2 x4  4 x  5
possui o mesmo
2x 4 .
3
3
3
 lim 4 
 0.
x 2 x  4 x  5
x 2 x

lim
4
-Limites Indeterminados
Considere a função
2 x  3x  2  
4
x  

.

g ( x) 
e que
2 x 4  3x  2
. Note que quando, x  
x3  4 x
x  4 x  
3
e assim teremos
então
2 x 4  3x  2 
lim

x 

x3  4 x
que também
representa um tipo de indeterminação.
6
2 x 4  3x  2
lim
x 
x3  4 x
Para calcular o limite
lim (an x n  an1x n1 
 a2 x 2  a1x  a0 )  lim an x n .
x
Assim,
iremos novamente utilizar o fato de que
x
2 x 4  3x  2
2 x4
2x

lim
 lim
 .
3
3
x 
x x
x 1
x  4x
lim
-Exercícios Resolvidos:
1) Calcule o limite
Resolução:
Temos que
2) Calcule o limite
2 x3  5 x  1
, caso exista.
x  x 4  5 x 3  3
lim
2 x3  5 x  1
2 x3
2
2

lim
 lim 
0.
4
3
4
x  x  5 x  3
x  x
x  x

lim
lim
x 
3x 4  2
x  3x  4
8
.
Resolução:
Temos que
lim
x 
3x 4  2
x8  3 x  4
 lim
x 
3x 4
x8
 lim
3 x4
x 
x4
 3 ¨.
8
x2
-Exercícios Propostos:
1) Para cada uma das funções abaixo determine o limite
os respectivos valores de
lim
h0
f ( a  h)  f ( a )
f ( x)  f (a )
e lim
x a
h
xa
para
a.
a) f ( x)  2 x, a  3;
b) f ( x)  x 2 , a  3;
d ) f ( x)  x 2  2 x, a  2; e) f ( x)  2 x 2  1, a  1;
g ) f ( x)  x3  1, a  1 h) f ( x)  2 x3 , a  2;
c) f ( x)  2 x 2 , a  1
f ) f ( x)  x 3 , a  2
i ) f ( x)  x 3  x 2 , a  3
2) Calcule os seguintes limites:
4 x5  9 x  7
a) lim 6
x 1 3 x  x 3  1
x2  5x  6
d ) lim
x 2
x2  4
x2  9
g ) lim 2
x 3 x  3 x
8  x3
x 2 x 2  2 x
j ) lim
m) lim
x 0
x4 2
x
3x 2  4 x
b) lim
x 2 4 x 2  14
x2  9
e) lim 2
x 3 x  5 x  6
(2  h) 2  4
h) lim
h 0
h
k ) lim
x 1
x 1
6 x 2  3  3x
c) lim
4 x2  1
x2  2
x2  5x  4
f ) lim 2
x 1 x  4 x  3
2 x
i ) lim
x 2 2  2 x
x 3
l ) lim
x 0
9  5x  4 x2  3
x
2 x 3
x 1 x 2  49
n) lim
7
3) Calcule os seguintes limites no infinito:
2 x3  5 x  1
x  x 4  5 x 3  3
a) lim
x
2
x  x  3 x  1
x3x
h) lim
x  x 2  3
d ) lim
k ) lim
x 
x4  2
x3
b) lim
x 
e) lim
x 
3x 4  2
x8  3 x  4
x2  1
3x  2

i ) lim x  x 2  1
x 
x2  2x  3
x  3 x 2  x  1
c) lim
g ) lim
x 

3x 4  x  1
l ) lim
x 
x4  5
j ) lim
x 

x2  1
3x  2
x 1  x  3

x9  1
m) lim 9
x  x  x 6  x 4  1
4) Calcule os seguintes limites infinitos:
x3  3x  1
a) lim 2
x  2 x  x  1
d ) lim (5  4 x  x 2  x5 )
x 
2x  1
x 0
x
x2  4
j ) lim 2
x 2 x  4 x  4
g ) lim
x 2  3x
b) lim 2
x 2 x  4
5 x3  6 x  1
e) lim
x  6 x 2  x  1
2x  3
h) lim 2
x 1 x  1
x 2  3x
k ) lim 2
x 3 x  6 x  9
x3  1
c) lim 2
x 1 x  2 x  1
5
f ) lim
x 3 3  x
2x  3
i ) lim 2
x 1 x  1
x 1
l ) lim
x 1
x 1
8
UNIVERSIDADE FEDERAL DA PARAÍBA
CAMPUS IV-CCAE
CURSO
DISCIPLINA
LICENCIATURA EM MATEMÁTICA
CÁLCULO DIFERENCIAL E INTEGRAL I
José Elias Dos Santos Filho
PROFESSOR
Funções Contínuas
- Introdução
 x2  1
x 1
, se x  1

, h( x)  x  1 , e a
, g ( x)   x  1
f ( x) 
x 1
 1,
se x  1

2
Inicialmente considere as funções
função
funções
 x  1, se  1
k ( x)  
. Abaixo você poderá observar as semelhanças entre os gráficos das
x

2,
se
x

1

f , g, k e h .
Gráfico da função
Observações sobre o Gráfico
Note que
f (1)
não existe, já que
Dom( f )  IR  {1} . Isso faz com que
tenhamos uma quebra no gráfico da função
no ponto
x  1 , na qual você pode observar.
Dizemos assim, que a função
contínua no ponto
não é
x 1.
Observe ainda que
lim f ( x)  2  f (1) .
x1
Note que agora, que temos
que
f ( x)
g (1)  1 ,
já
Dom( g )  IR , mas, no entanto, ainda
continuamos com uma quebra no gráfico da
função no ponto
x  1 , na qual você pode
observar. Dizemos assim, que a função
g ( x)
não é contínua no ponto
Observe ainda que
x 1.
lim g ( x)  2  g (1) .
x1
1
Observe que o gráfico da função
k ( x)
possui uma quebra no seu gráfico de forma
mais clara, isso é devido ao fato de que
lim k ( x)  lim k ( x) , ou seja, lim k ( x)
x1
x 1
x1
não existe. Dizemos assim que a função
k ( x)
não é contínua no ponto
Note ainda que a função
no ponto
k ( x)
x 1.
esta definida
x  1 , a saber,
k ( x)  2  lim k ( x) .
x1
Obseve que a função
h( x )
não apresenta
quebra no gráfico no ponto
x 1
diremos que a função
é continua no
ponto
h( x )
x  1.
A continuidade da função
ponto
e assim
x 1
h(1)  2
h( x)  x  1
no
é devido ao fato de que
e que
lim h( x)  2 , ou seja,
x1
lim h( x)  2  h(1) .
x1
- Funções Contínuas
Com base nos gráfico apresentados anteriormente podemos apresentar a definição de continuidade
de uma função num ponto.
Definição: Dizemos que uma função
(I)
f (a)
(II)
lim f ( x)
(III)
x a
f
é contínua em
xa
se as seguintes condições forem satisfeitas:
existe
existe
lim f ( x)  f (a)
xa
Exemplo 1: Podemos verificar que a função
não esta definida no ponto
contínua no ponto
x2  1
f ( x) 
x 1
x  1 , ou seja, f (1)
não é contínua no ponto
não existe. Portanto a função
x  1 , pois a função
f ( x) 
x2  1
x 1
não é
x  1 . (Veja o gráfico na tabela anterior)
2
Exemplo 2: Considerando a função
mas
lim k ( x)
x 1
existe, ou seja,
k (1)  2 ,
 x  1, se  1
lim k ( x)  lim k ( x) . Portanto a função k ( x)  
x1
x1
 x  2, se x  1
não existe, já que
é contínua no ponto
 x  1, se  1
, vemos que k (1)
k ( x)  
 x  2, se x  1
não
x  1 . (Veja o gráfico na tabela anterior)
Exemplo 3: Considere a função
 x2  1
, se x  1

.
g ( x)   x  1
 1,
se x  1

Note que,
(I)
g (1)  1 existe
(II)
lim g ( x)  2
x1
existe
No entanto, note que
Portanto a função
lim g ( x)  2  g (1) .
x1
 x2  1
, se x  1

g ( x)   x  1
 1,
se x  1

não é contínua no ponto
x  1 . (Veja o gráfico na
tabela anterior)
Exemplo 4: Considerando a função
(I)
h(1)  2
(II)
(III)
h( x)  x  1 teremos:
existe
lim h( x)  lim( x  1)  2
x1
x1
existe
lim h( x)  h(1)  2
x1
Portanto a função
h( x)  x  1 é contínua no ponto x  1 . (Veja o gráfico na tabela anterior)
Uma função é contínua em um intervalo
[a, b] se e somente se for contínua em cada ponto do
intervalo. Uma função contínua é aquela que é contínua em cada ponto de seu domínio.
Note que o gráfico da função
função
h( x)  x  1 é uma reta que não possui quebra no gráfico. Assim, a
h( x)  x  1 é contínua em todos os pontos do domínio da função Dom(h)  IR , ou
simplesmente,
h( x)  x  1 é uma função contínua.
- Continuidade dos Polinômios
Se
P( x)  an xn  an1x n1 
lim P( x)  P(c)
xc
para todo
 a2 x 2  a1x  a0 , com an  0
é um polinômio qualquer, então
c  IR , ou seja, um polinômio qualquer é contínuo para todo ponto
x  c  IR .
3
-Propriedades de Funções Contínuas
Se as funções
f g
(I)
f
e
g
são contínuas em
x  c;
é contínua em
(II)
f g
(III)
f .g
(IV)
f
g
é contínua em
x  c;
x  c;
é contínua em
é contínua em
x  c , então :
x  c , se g (c)  0 .
-Composta de Funções Contínuas
Se
f
é contínua
xc
e
f ( x)
cujo gráfico está representado abaixo:
g
é contínua em
f (c) , então a composta g ( f ( x))
é composta em
x  c.
-Exercícios Resolvidos
1) Considere uma função
Com base no gráfico da função responda:
a)
f ( x)
é contínua no ponto
x  2 ? Justifique.
b)
f ( x)
é contínua no ponto
x  1 ? Justifique.
c) Qual é o domínio da função
f ( x)
e m quais pontos de seu domínio a função é contínua?
Resolução:
a) Com base no gráfico da função temos que:
(I)
f (2)  1 , existe
Como
(II)
lim f ( x)  1  lim f ( x) , ou seja, lim f ( x)  1
x2
x 2
x2
existe.
lim f ( x)  1  f (2) , então a função é contínua em x  2 .
x2
Graficamente vemos que o gráfico da função não possui quebra no ponto
é contínua em
x  2 , ou seja, a função
x  2.
b) Pelo gráfico da função teremos:
(I)
f (1)  2
(II)
lim f ( x)  1  lim f ( x)  3 , ou seja, lim f ( x)
x1
Portanto, a função
f ( x)
x1
x1
não é contínua no ponto
não existe.
x  1.
4
c) Vemos que a função
f ( x)
esta definida no intervalo
Já vimos que a função não é contínua no ponto
existe uma quebra no gráfico da função no ponto
[5, 4]
x 1
e assim,
Dom( f )  [5,4] .
e com base no gráfico, vemos que também
x  2 , ou seja, f ( x)
também não é contínua no ponto
x  2 .
Veja que
f (2)  0
diferente do limite
Portanto,
lim f ( x)
x2
não existe, já que
lim f ( x)  3
x2
que é
lim f ( x)  0 .
x2
é continua no conjunto
f ( x)
2) Mostre que a função
Resolução: Se
existe, mas no entanto
g ( x)  1  1  x 2
C  [5,4]  {2,1} .
é contínua no intervalo
[1,1] .
1  a  1, então, usando as Propriedades dos Limites, temos


x a
xa
se
lim g ( x)  lim 1  1  x 2  1  lim 1  x 2  1  lim(1  x 2 )  1  1  a 2  g (a)
xa
Assim,
xa
g ( x)
é contínua em
Vamos agora verificar se a função
x a
1  a  1.
g ( x)  1  1  x 2
é contínua nos extremos do intervalo
[1,1] , ou seja, x  1 e x  1 .
Para o ponto
x  1 temos que lim g ( x)  g (1) . Veja que não faz sentido calcular
x1
lim g ( x) . (Veja o gráfico abaixo)
x1
Analogamente, para o ponto
x 1
temos que
lim g ( x)  g (1) . Veja que não faz sentido calcular
x1
lim g ( x) . (veja o gráfico abaixo)
x1
Portanto,
g ( x)  1  1  x 2
é contínua no intervalo
[1,1] . Veja o Graco da função abaixo.
5
3)Determinar
Resolução:
(I) Temos que
 x 2  5 x  4, se x  4
m  IR de modo que f ( x)  
, se x =4
3m
seja contínua em x = 4.
f (4)  3.4  12
(II) Cálculo do limite de
f ( x) :
lim f ( x)  lim( x 2  5x  4)  42  5  4  6  2
x4
x4
(III) Para que a função seja contínua em x = 4, devemos ter
lim f ( x)  f (4)  2  3m  m 
x 4
lim f ( x)  f (4)
x4
2
.
3
Portanto, para que a função seja contínua em x=4 devemos ter
4) Verificar se a função
f ( x) 
x2  4
x2
e assim:
m
2
.
3
é contínua no ponto em x =3 e no ponto x=2.
Resolução:
(I) Temos
(II)
32  4
f (3) 
 5.
3 2
( x  2) ( x  2)
x2  4
 lim
 lim( x  2)  5
x3 x  2
x3
x3
( x  2)
lim
Logo, f(x) é contínua em x=3.
Observe que
f ( x)
não é contínua em x=2, pois, não existe
f (2) .
6
-Exercícios Propostos:
1) Complete a afirmação:
“A função
f
é contínua em
2) Considere as funções
xc
se estiver definida
1, se x  4
f ( x)  
1, se x  4
e
f ( x)
é contínua em
x  4 ? Justifique.
b) A função
g ( x)
é contínua em
x  4 ? Justifique.
c) A função
f ( x)  g ( x)
d) A função
g ( f ( x))
4) Considere a função
Com base no gráfico de
x  4 ? Justifique.
x , se houver, a função f ( x) 
h( x )
e ____________________.”
x  4 ? Justifique.
é contínua em
3) Para quais valores de
xc
4 x  10, se x  4
.
g ( x)  
6, se x  4
a) A função
é contínua em
f (c) , existir lim f ( x)
x 2  16
x2  5x  4
é descontínua?
cujo gráfico esta representado abaixo:
h( x )
responda:
a) Qual o domínio da função?
b) A função é contínua no ponto
x  0 ? E no ponto x  1 ? Justifique.
c) Em quais pontos a função é contínua?
5) Encontre um valor para a constante
7 x  2, se x  1
a ) f ( x)   2
se x  1
kx ,
k , se possível, que faça a função ficar contínua em toda parte.
kx 2 , se x  2
b) g ( x )  
2 x  k , se x  2
 x2  9
, se x  3

c ) h( x )   x  3
 k,
se x  3

7