COLÉGIO PEDRO II - UNIDADE SÃO CRISTÓVÃO III
MATEMÁTICA – 1ª SÉRIE – AULA DE APOIO
COORDENAÇÃO: COORDENADORA: MARIA HELENA M. M. BACCAR
LISTA DE EXERCÍCIOS DE APOIO – 2ª CERTIFICAÇÃO - GABARITO
1
, sen45° = cos45° =
2
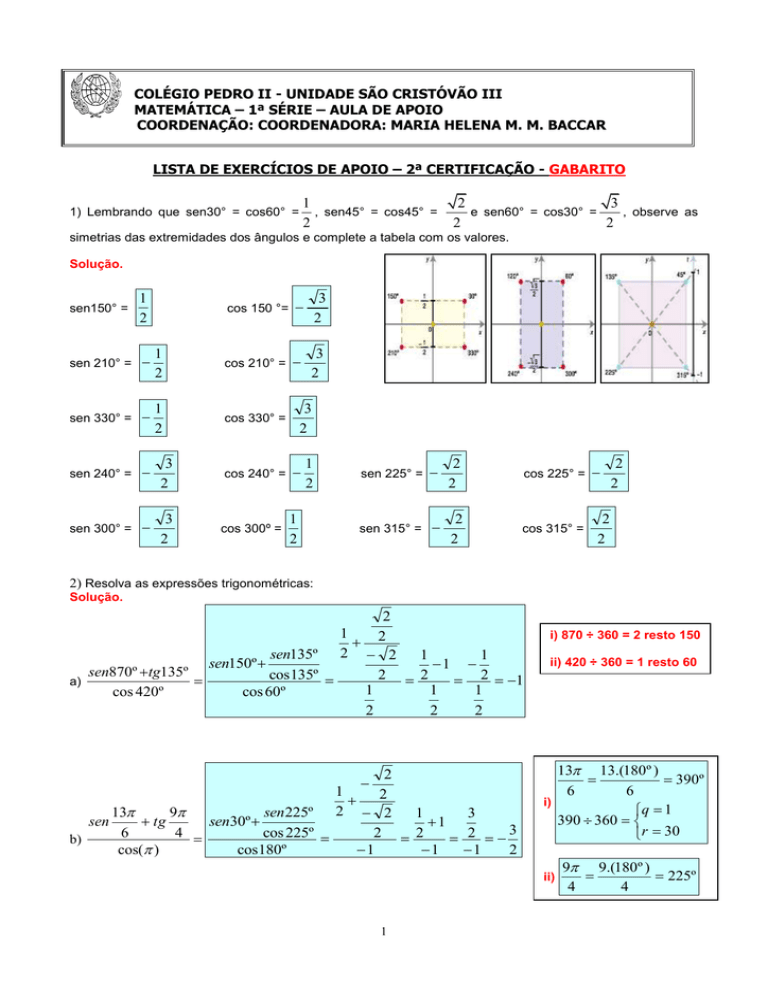
1) Lembrando que sen30° = cos60° =
2
3
e sen60° = cos30° =
, observe as
2
2
simetrias das extremidades dos ângulos e complete a tabela com os valores.
Solução.
sen150° =
1
2
cos 150 °=
3
2
3
2
sen 210° =
1
2
cos 210° =
sen 330° =
1
2
cos 330° =
3
2
sen 240° =
3
2
cos 240° =
sen 300° =
3
2
cos 300º =
1
2
1
2
sen 225° =
2
2
cos 225° =
sen 315° =
2
2
cos 315° =
2
2
2
2
2) Resolva as expressões trigonométricas:
Solução.
2
1
2
sen135º 2 2
1
1
sen150º
1
sen870º tg135º
cos135º
2 2
2 1
a)
1
1
1
cos 60º
cos 420º
2
2
2
2
1
2
2
sen 225º
13
9
2
1
3
sen
tg
sen30º
1
3
6
4
cos 225º
2 2
2
b)
cos180º
1
1
1
2
cos( )
i) 870 ÷ 360 = 2 resto 150
ii) 420 ÷ 360 = 1 resto 60
13 13.(180º )
390º
6
6
i)
q 1
390 360
r 30
ii)
1
9 9.(180º )
225º
4
4
3) Um pêndulo tem 15 cm de comprimento e, no seu movimento, suas posições extremas formam um ângulo
de 60º. Qual é o comprimento do arco que a extremidade do pêndulo descreve?
Solução. Repare que a questão está em encontrar o comprimento do arco determinado por um ângulo
central de 60º em uma circunferência de raio 15cm. Exprimindo 60º em radianos, temos:
3
rad . A
fórmula s = r. permite calcular: s = 15.(3,14)/3 ~ 15,7cm ou 5cm.
4) Qual é o comprimento de um arco correspondente a um ângulo central de 60º contido numa circunferência
de raio 1,5cm?
Solução. A fórmula com comprimento do arco é: S = r.rad. No caso do ângulo de 60º devemos passálo para radianos. Temos: S (1,5).
6
1,57cm
5) Ache o perímetro de um triângulo que possui lados de 5cm e 7 cm, entre os quais se forma um ângulo cujo
3
seno vale
5
.
Solução. Para encontrar o terceiro lado aplicamos a lei dos cossenos. Aplicando a relação
fundamental: sen x cos x 1 descobrimos o cosseno do ângulo, com a informação sobre o valor
2
2
do seno:
4
cos x
9
16
3
5
sen 2 x cos 2 x 1 cos 2 x 1 cos x 1
. Substituindo na
25
25
5
cos x 4
5
2
Lei dos Cossenos, temos:
4
2
a 74 56 a 18 3 2 .
5
i) a 5 7 2(5)( 7).
2
2
2
O perímetro do triângulo é: 5 7 3 2 12 3 2 3(4
2 )cm
4
2
a 74 56 a 130 .
5
ii) a 5 7 2(5)( 7).
2
2
2
O perímetro do triângulo é:
5 7 130 12 130cm
6) Calcule as medidas dos ângulos B e C de um triângulo ABC, sendo  = 15º, a = 1 e b = 1+ 3 .
Solução. Conhecendo dois lados e um ângulo de um triângulo, podemos calcular os outros dois
aplicando a Lei dos Senos e a relação de Tales para o 3º ângulo. O sem 15º pode ser calculado pela
relação: sen15º sen (45º 30º ) sen 45º cos 30º sen30º cos 45º
1
1 3
senB
sen15º
senB
2 3 1 2
.
.
2 2 2 2
B 45º
6 2
2 2
2
.(1 3 )
4
4
2
B 135º
i) Se B = 45º então C = 180º - (45º + 15º) = 120º
ii) Se B = 135º então C = 180º - (135º + 15º) = 30º
2
6 2
. Logo,
4
7) No quadrilátero ABCD, em que os ângulos B e D são retos e os lados têm as medidas indicadas, o valor
de sen é:
Solução. Dividindo o quadrilátero da forma indicada aplicamos a Lei dos
cossenos e a Lei dos senos em relação ao lado após calcular o lado “b”
oposto ao ângulo reto.
i) b
ii)
iii)
(2 x) 2 x 2 5 x 2 x 5
A
A
A 2 5
x 2 4 x 2 5 x 2 2(2 x)( x 5 ) cos x 2 9 x 2 4 x 2 5 cos cos
.
5
2
2
2
x 5
sen90º
Logo,
x
x
5
A
sen
5
A
2 x 5
sen
2
A
A
A
A
A
A
2 5 5 4
A A
sen A sen sen cos sen cos 2.sen . cos 2.
.
.
2
2
2
2
2
2
5 5
5
2 2
8) Um triângulo ABC é tal que AB = 3
2 , Â = 45º e Ĉ = 30º. A soma dos lados AC e BC do triângulo é:
Solução. Pelas informações do problema, podemos aplicar a Lei dos Senos para o lado BC oposto ao
ângulo A e lado AB oposto a C:
i)
3 2
BC
BC
sen30º sen 45º
2
2 3 6
1
1
2
2
(3 2 ).
2
62 3 2 ( AC ) 2 2(3 2 ).( AC ). cos 45º
2
36 18 ( AC ) 2 2(3 2 ).( AC ).
2
ii)
2
2
36 18 ( AC ) 6 AC ( AC ) 6 AC 18 0
AC 3 3 3
(6) (6) 2 4((1)( 18) 6 108 6 6 3
AC
2(1)
2
2
AC 3 3 3; ( 0)
Logo AC + BC = 6 3 3 3(2
3)
3












