1. (UF-MG) Na figura, OAB, OBC e OCD são triângulos retângulos

9º
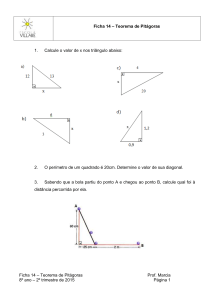
Geometria
Junior
Aval. Mensal
05/03/12
1. (UF-MG) Na figura, OAB, OBC e OCD são triângulos retângulos em A, B e C,
respectivamente. AO = AB = CD = 1m. Qual a medida do segmento OD?
2. Num losango as diagonais medem 16 cm e 12 cm. Determine a medida do lado
desse losango e o seu perímetro.
3. Determine a medida do lado de um quadrado cuja área é 5m 2.
4. Calcule a medida da diagonal de um quadrado cujo lado mede 1cm.
5. Você aprendeu que, dados três números, se a soma dos quadrados dos dois
menores for igual ao quadrado do maior, esses três números formam uma trinca
ou terno pitagórico, ou seja, representam as medidas dos três lados de um
triângulo retângulo.
Você viu também que o triângulo retângulo já era conhecido de povos anteriores
aos gregos. Inclusive há registros de tabelas contendo ternos pitagóricos. Uma
delas é a tableta babilônica Plimpton 322 – nome do arqueólogo inglês que a
descobriu. Nela há uns 15 ternos de números inteiros para os quais a soma de
dois quadrados deles é igual ao quadrado do terceiro. Essa tableta foi gravada
mais de 1 000 anos antes do nascimento de Pitágoras! Um desses ternos é 45,
60 e 75, que equivale à nossa famosa trinca 3, 4 e 5.
Encontre outro terno pitagórico.
6. O chamado Papiro Matemático Cairo foi desenterrado em 1938 e investigado em
1962. O papiro, que data de 300 a.C. aproximadamente, contém 40 problemas
de Matemática, nove dos quais lidam exclusivamente com o teorema de
Pitágoras, e mostra que os egípcios dessa época não só sabiam que o triângulo
3, 4, 5 é retângulo, mas que também acontecia o mesmo para os triângulos 5,
12, 13 e 20, 21, 29. Resolva um dos problemas desse papiro.:
Uma escada de 10 cúbitos está com seus pés a 6 cúbitos da parede. Que altura
a escada alcança?
7. (Fatec-SP) Na figura, ABCD é um retângulo. Qual a medida do segmento EF?
8. Problema “Bambu quebrado“, popular na China:
Se um bambu de 32 cúbitos de altura é quebrado pelo vento, de modo que a
ponta encontra o chão a 16 cúbitos da base, a que altura a partir do chão ele foi
quebrado?
9. Problema “O pavão e a cobra“:
No pé de um pilar de 15 cúbitos de altura há um buraco de cobra e em seu cume
está empoleirado um pavão. Vendo a cobra, a uma distância da coluna igual ao
triplo da altura do pilar, rastejando-se para o seu buraco, o pavão arremete contra
ela. A quantos cúbitos do buraco da cobra se encontram, se ambos percorrem
distâncias iguais?
10. Uma escada de 2,5m deverá alcançar uma luminária a 2m numa parede. A
quantos metros da parede deverá ficar o pé da escada? Faça um desenho para
representar a situação dada.