Capítulo 25: Capacitância

Capítulo 25:
Capacitância
Cap. 25: Capacitância
Índice
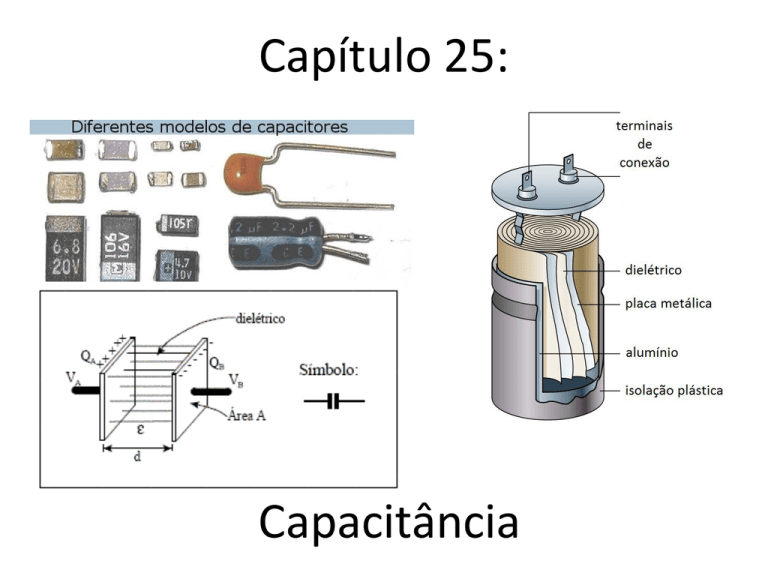
 Capacitor
Capacitância
 Calculo da capacitância
 Capacitores em paralelo e em série
 Energia armazenada em um campo elétrico
 Capacitor com dielétrico
 Dielétricos: uma visão atômica
 Dielétricos e a Lei de Gauss
Cap. 25: Capacitância
Capacitor
Dois condutores isolados entre si e do ambiente, formam um capacitor. Quando
este dispositivo está carregado, as cargas nos condutores ou placas, tem o mesmo
valor absoluto q, e sinais opostos. Este tipo de dispositivo serve para armazenar
cargas elétricas e fornecê-las em um momento futuro.
Cap. 25: Capacitância
Capacitância
 Sempre podemos escrever a diferença de potencial V, em termos da carga q.
V q
C
 C é uma constante geométrica denominada de Capacitância. No SI sua unidade
de medida é o coulomb por volt denominado de farad [C/V = F].
Cap. 25: Capacitância
Capacitância
• Quando a chave S é fechada passa a ter corrente elétrica entre os terminais devido
ao campo elétrico criado pela bateria.
• Os elétrons se deslocam da placa a do capacitor para o terminal positivo da
bateria e a placa a fica positivamente carregada.
• Os elétrons se deslocam do terminal negativo da bateria para a placa b e ela fica
negativamente carregada. O capacitor está completamente carregado quando a
diferença de potencial do capacitor atingir o mesmo valor da bateria.
Obs: Para análise futura: as cargas não podem passar de uma placa para a outra e o capacitor
conserva a carga.
Cap. 25: Capacitância
Cálculo da Capacitância
Capacitor de placas paralelas
 Calcular o campo elétrico, E, entre as placas
em função de q.
 
qint
 E  ndA 
q   0 EA
0
 Calcular a diferença de potencial V entre as
placas em função de E.
  d
V    E  ds   Eds
V  Ed
0
E = cte entre as placas e
tem sentido oposto ao
de ds.
 Calcular C a partir dos valores de q e V.
V q
C
Cq
V

 0 EA
Ed
C
0 A
d
A é a área de uma das placas do Capacitor e d é a distância que separa as placas.
Cap. 25: Capacitância
Cálculo da Capacitância
Capacitor Cilíndrico
 Calcular o campo elétrico, E, entre as placas em
função de q.
 
qint
 E  ndA 
0
q   0 EA
q   0 E 2rL
 Calcular a diferença de potencial V entre as placas
em função de E.
 
V   E  ds
V
q
2 0 L
ln r |ba
 Calcular C a partir
dos valores de q e V.
a
V 
b
V
q
2 0 rL
q
2 0 L
Cq
V
(dr )
 a
ds  -dr
ln b

q
q
2 0 L
 a
ln b
C
2 0 L
 a
ln b
Cap. 25: Capacitância
Cálculo da Capacitância
Capacitor Esférico
 Calcular o campo elétrico, E, entre as placas em função
de q.
q   0 EA
 
qint
 E  ndA 
E
q   0 E 4r
0
2
q
4 0 r 2
 Calcular a diferença de potencial V entre as placas em
função de E.
 
V   E  ds
a
V 
b
q
4 0 r
2
(dr )
q ba
V


4 0  ab 
q 1 1
V
| 
  
4 0 r
4 0  a b 
q
a
b
 Calcular C a partir
dos valores de q e V.
Cq
ds  -dr
V

q
q ba


4 0  ab 
 ab 
C  4 0 

ba
Cap. 25: Capacitância
Cálculo da Capacitância
A Esfera Isolada
Consideremos um capacitor esférico com a casca
esférica externa de raio infinito!
b
 ab 
C  4 0 

ba
a
C  4 0
1 a

C  4 0 R
b

R é o raio da esfera, neste caso R = a.
Cap. 25: Capacitância
Capacitores em Paralelo
Capacitores ligados em paralelo: A diferença de
potencial é a mesma em todos os capacitores,
inclusive no capacitor equivalente!
 A carga total armazenada no circuito (carga do
capacitor equivalente) é igual à soma da carga de
cada um dos capacitores!
Calculando as cargas em cada capacitor.
q1  C1V
q2  C2V
q3  C3V
q  q1  q2  q3
CV  C1V  C2V  C3V
C  C1  C2  C3
n
Ceq   C j
j 1
Cap. 25: Capacitância
Capacitores em Série
 Capacitores ligados em série: A carga em cada um dos
capacitores é igual, inclusive no capacitor equivalente.
 A diferença de potencial do capacitor equivalente é
definida pela soma das diferenças de potencial de cada
um dos capacitores.
q  CV
Calculando a diferença de potencial.
q
V  V1  V2  V3
1
Ceq
Ceq
 1
1
C1
 q
 1
C1
C2
n
Ceq
 1
j 1
Cj
q
 1
C2
C3
q
C3
Cap. 25: Capacitância
Cálculo da Capacitância
Exemplo 2) pg. 119
a) Determine a capacitância equivalente da combinação de capacitores que
aparece na figura abaixo, na qual, C1 = 12 F, C2 = 5,30 F e C3 = 4,50 F.
Passo 1: Em paralelo.
Ceq p  C1  C2  12  5,3  17,3F
Passo 2: Em série.
1
Ceq
 1
Ceq p
 1
C3
Ceq  3,57F
b) Determine a carga acumulada no capacitor C1
quando a diferença de potencial é de 12,5 V.
Encontrar a carga equivalente emC123 que será a mesma em C3 e Ceq p
Calcular a diferença de potencial entre A e B.
q123  CeqV  (3,57 106 )12,5  44,6C
q123  q12  Ceq pVab
Vab  q12 / Ceq p  2,58V
q1  C1Vab  31C
Cap. 25: Capacitância
Cálculo da Capacitância
Exemplo 3) pg. 120
O capacitor 1, com C1 = 3,55 F, é carregado por uma bateria com
diferença de potencial de 6,3 V. A bateria é removida e o
capacitor é ligado, como na figura ao lado, a um capacitor 2 com
C2 = 8,95 F. Determine a carga dos capacitores depois que o
equilíbrio é atingido.
5
• Calcular q0 quando apenas o capacitor 1 é carregado. q0  C1V  2,24 10 C
• Após a chave ser fechada, sem a bateria, q0 = q1 + q2, assim como, V1 = V2 (Circuito em
Paralelo).
q1
q1
C1
q1 
C1


q2
C2
(q0  q1 )
C1q0
q1  6,35C
C2
(C2  C1 )
q2  q0  q1  16C
Cap. 25: Capacitância
Energia armazenada em um
campo elétrico
 A energia potencial armazenada em um capacitor carregado está associado
ao campo elétrico que existe entre as placas.
Para transferir uma carga dq’ ao capacitor
(imaginando o carregamento do capacitor), é
necessário que um agente externo realize um
trabalho dW descrito como:
V
q
Wag
q
q
q'
q2
 dWag  0 Vdq'  0 C dq'  2C
q2
Wag 
2C
Como o capacitor estava inicialmente carregado, a variação
de Energia Potencial pode ser descrita pela energia final
acumulada no capacitor durante o processo de carga!
q2 1
U  Wag 
 CV 2
2C 2
Cap. 25: Capacitância
Densidade de Energia
 A densidade de energia, u, é definida pela razão entre a energia acumulada e
o volume necessário para acumulá-la.
U
u
Volume
 Para um capacitor de placas paralelas:
1
CV 2
2

V
u 2
 0 2
Ad
2d
C
1
u  0E2
2
0 A
d
Densidade de Energia
Cap. 25: Capacitância
Energia armazenada em um
campo elétrico
Exemplo 5) pg 124
Uma esfera condutora isolada de raio 6,85 cm possui uma carga de 1,25 nC. a)
Qual é a energia potencial armazenada no campo desse condutor? b) Qual a
densidade de energia na superfície da esfera?
Uma esfera isolada possui capacitância dada por:
U
q2
2(4 0 R)
C  4 0 R
 103mJ
Sabendo o Campo Elétrico na superfície da esfera, temos:
2
2


1
1
q
q
3

u   0 E 2   0 


25
,
4
mJ
/
m
2
2  4 0 R 2 
(32 2 0 R 4 )
Cap. 25: Capacitância
Capacitor com um Dielétrico
Michael Faraday, constatou que em um capacitor contendo um material dielétrico isolantes, plásticos, óleo mineral... – a capacitância é multiplicada por uma constante
dependente da composição do dielétrico. Essa constante é chamada de constante
dielétrica, . Sendo assim, sempre que uma região for totalmente preenchida por um
material dielétrico de constante dielétrica , o valor da permissividade do vácuo, 0, deve
ser substituído por  0 em todas as equações.
 0  0
C

C0
Vantagens do uso dos dielétricos em capacitores:
 Facilidade em manter as placas dos capacitores separados.
 Aumento na capacitância, e por consequência, aumento no
acumulo de cargas.
 Permite aumento na diferença de potencial entre as placas
sem que haja ruptura.
Rigidez dielétrica: Campo elétrico máximo que o material
pode tolerar sem que ocorra a ruptura.
Cap. 25: Capacitância
Capacitor com um Dielétrico
Exemplo 6) pg. 126
Um capacitor de placas paralelas cuja capacitância C é 13,5 pF é carregado por uma bateria
até que haja uma diferença de potencial V = 12,5 V entre as placas. A bateria é desligada e
uma placa de porcelana (κ = 6,5) é introduzida entre as placas. Qual a energia potencial do
capacitor (antes e depois) da introdução da placa cerâmica? (1100 pJ; 160 pJ)
Antes da introdução da placa:
1
U 0  C0V 2
2
U 0  1100 pJ
Depois da introdução da placa: A carga é a mesma da situação inicial!
U0
q2
q2
U


2C 2C0 
U  160 pJ
Cap. 25: Capacitância
Natureza dos Dielétricos
As moléculas dos materiais dielétricos podem ser polares ou apolares. Na presença de um
campo elétrico todas as moléculas de um dielétrico apresentam polarização. Sendo assim,
quando um campo elétrico é aplicado, os dipolos elétricos se alinham parcialmente na
direção do campo. Esse alinhamento é parcial, por causa da agitação térmica que tende a
desorientar os dipolos.
Cap. 25: Capacitância
Natureza dos Dielétricos
Do ponto de vista de um capacitor:
q1  C0V1
Se q = cte
Se V = cte
V diminui
q aumenta
q2  C0V2
Cap. 25: Capacitância
Natureza dos Dielétricos
Analise das cargas de um capacitor com a mesma diferença de potencial
Sem dielétrico
q0 +
+
+
+
+
Com dielétrico
-  q0
-
q0 = carga do capacitor sem polarizador
q = carga livre induzida na placa do
capacitor devido a inserção do dielétrico.
q’ = carga de polarização (fixa na sup. Do
dielétrico).
q0  q  q '
q
q
 q´
q´
Cap. 25: Capacitância
Natureza dos Dielétricos
Na presença de um material dielétrico, podemos escrever a lei de Gauss da seguinte
forma:
 
qint q  q'
 E  ndA  
0
E
q  q'
0 A
0
q é a carga livre (placa metálica).
q’ é a carga de polarização
(induzida no dielétrico).
Sabemos que na presença de um material
dielétrico o campo elétrico diminui:
E
q

q
0 A
 q  q'
 
q

E

n
dA


0
 
 D  ndA  q
E E0
E  E0 / 


D   0E
Vetor Deslocamento Elétrico
Cap. 25: Capacitância
Natureza dos Dielétricos
Exemplo 7) pg. 129
A figura ao lado mostra um capacitor de placas paralelas com área das placas A, distância
de separação d, carregado por meio de uma diferença de potencial V0 de uma bateria. A
bateria é removida e é introduzido um dielétrico de espessura b, com constante dielétrica
. Suponha que A = 115 cm2, d= 1,24 cm, V0 = 85,5 V, b = 0,78 cm e  = 2,61. Determine:
a) Qual a capacitância C0 antes da introdução do dielétrico?
C0 
0 A
d
C0  8,21 pF
b) Qual o valor da carga das placas?
q  C0V0
q  702 pC
c) Qual é o valor do campo elétrico entre as placas e o dielétrico?
 Na região sem a presença do dielétrico,  = 1, temos:
 
q
 E  ndA 
0
q
E
0 A
E  6,9kV / m
Cap. 25: Capacitância
Natureza dos Dielétricos
Exemplo 7) pg. 129 A = 115 cm2, d= 1,24 cm, V0 = 85,5 V, b = 0,78 cm e  = 2,61.
C0 = 8,21 pF, q = 702 pC e E0 = 6,9 kV/m.
d) Qual é o valor do campo elétrico dentro do dielétrico?
 
 0  E1  ndA  q
E1 
E1  2,64kV / m
q
0 A
e) Qual é a diferença de potencial entre as
placas depois da introdução do dielétrico?

 
V1   E  ds  E0 (d  b)  E1b

V1  52,3V
f) Qual é a capacitância do capacitor com o dielétrico?
 A carga antes e depois da inserção é a mesma!
C1  q
V1
 13,4 pF
Cap. 25: Capacitância
Lista de Exercícios
5, 7, 12, 13, 15, 17, 19, 25, 27, 29, 33, 35, 37,
45, 49, 50, 53, 54, 63.
Referências
HALLIDAY, D.; RESNICK, R.; WALKER, J.; Fundamentos
Eletromagnetismo. 8a ed. Rio de janeiro: LTC, 2009. v3.
de
Física:
TIPLER, P. A.; Física para Cientistas e Engenheiros. 4a ed, LTC, 2000. v2.
SEARS, F.; ZEMANSKY, M.W.; YOUNG, H.; FREEDMAN, R.A.; Física:
Eletromagnetismo. 12a ed. São Paulo: Pearson Addison Wesley, 2008. v3.