Lista - Revisão 2º Trimestre

Lista de Exercícios - Geometria Plana (1.ºAno)
Questão 1:(G1 - cps 2014) A Jornada Mundial da Juventude (JMJ) aconteceu no Rio de Janeiro, em julho
de 2013, e atraiu visitantes do Brasil e de vários outros países.
Segundo a Prefeitura do Rio, 3,2 milhões de pessoas compareceram à cerimônia de encerramento da
JMJ, que ocorreu na Praia de Copacabana.
(folha.uol.com.br/poder/2013/07/1318073-calculo-oficial-de-3-milhoes-de-pessoasem-copacabana-esuperestimado-diz-datafolha.shtml Acesso em: 16.08.2013. Adaptado)
A área da superfície ocupada pelas pessoas que compareceram à cerimônia de encerramento da JMJ
equivale à área da superfície de cerca de N campos de futebol do estádio do Maracanã.
Sabendo-se que o campo de futebol do Maracanã tem forma retangular com dimensões de 105 metros
por 68 metros e adotando-se que, em uma concentração de grande porte como essa, um metro
quadrado é ocupado por 4 pessoas, em média; então, considerando os dados apresentados, o número
inteiro positivo mais próximo de N será
a) 45.
b) 57.
c) 112.
d) 136.
e) 144.
Questão 2:(Enem 2013) O dono de um sítio pretende colocar uma haste de sustentação para melhor
firmar dois postes de comprimentos iguais a 6m e 4m. A figura representa a situação real na qual os
postes são descritos pelos segmentos AC e BD e a haste é representada pelo EF, todos perpendiculares
ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que
serão instalados.
Qual deve ser o valor do comprimento da haste EF?
a) 1m
b) 2 m
c) 2,4 m
d) 3 m
e) 2 6 m
Questão 3:(Enem 2012) Em 20 de fevereiro de 2011 ocorreu a grande erupção do vulcão Bulusan nas
Filipinas. A sua localização geográfica no globo terrestre é dada pelo GPS (sigla em inglês para Sistema
de Posicionamento Global) com longitude de 124° 3’ 0” a leste do Meridiano de Greenwich.
Dado: 1° equivale a 60’ e 1’ equivale a 60”.
PAVARIN, G. Galileu, fev. 2012 (adaptado)
A representação angular da localização do vulcão com relação a sua longitude da forma decimal é
a) 124,02°.
b) 124,05°.
c) 124,20°.
d) 124,30°.
e) 124,50°.
Questão 4:(Enem 2012) Em exposições de artes plásticas, é usual que estátuas sejam expostas sobre
plataformas giratórias. Uma medida de segurança é que a base da escultura esteja integralmente
apoiada sobre a plataforma. Para que se providencie o equipamento adequado, no caso de uma base
quadrada que será fixada sobre uma plataforma circular, o auxiliar técnico do evento deve estimar a
medida R do raio adequado para a plataforma em termos da medida L do lado da base da estatua.
Qual relação entre R e L o auxiliar técnico deverá apresentar de modo que a exigência de segurança seja
cumprida?
a) R ≥ L/ 2
b) R ≥ 2L/π
c) R ≥ L/ π
d) R ≥ L/2
(
e) R ≥ L/ 2 2
)
Questão 5:(Enem 2011)
O polígono que dá forma a essa calçada é invariante por rotações, em torno de seu centro, de
a) 45°.
b) 60°.
c) 90°.
d) 120°.
e) 180°.
Questão 6:(Enem 2011) O atletismo é um dos esportes que mais se identificam com o espírito olímpico.
A figura ilustra uma pista de atletismo. A pista é composta por oito raias e tem largura de 9,76 m. As
raias são numeradas do centro da pista para a extremidade e são construídas de segmentos de retas
paralelas e arcos de circunferência. Os dois semicírculos da pista são iguais.
Se os atletas partissem do mesmo ponto, dando uma volta completa, em qual das raias o corredor
estaria sendo beneficiado?
a) 1
b) 4
c) 5
d) 7
e) 8
Questão 7:(Enem 2010) A loja Telas & Molduras cobra 20 reais por metro quadrado de tela, 15 reais por
metro linear de moldura, mais uma taxa fixa de entrega de 10 reais.
Uma artista plástica precisa encomendar telas e molduras a essa loja, suficientes para 8 quadros
retangulares (25 cm x 50 cm). Em seguida, fez uma segunda encomenda, mas agora para 8 quadros
retangulares (50 cm x 100 cm).
O valor da segunda encomenda será
a) o dobro do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
b) maior do que o valor da primeira encomenda, mas não o dobro.
c) a metade do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
d) menor do que o valor da primeira encomenda, mas não a metade.
e) igual ao valor da primeira encomenda, porque o custo de entrega será o mesmo.
Questão 8:(Enem 2009) Rotas aéreas são como pontes que ligam cidades, estados ou países. O mapa a
seguir mostra os estados brasileiros e a localização de algumas capitais identificadas pelos números.
Considere que a direção seguida por um avião AI que partiu de Brasília – DF, sem escalas, para Belém,
no Pará, seja um segmento de reta com extremidades em DF e em 4.
Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção que forma um
ângulo de 135o graus no sentido horário com a rota Brasília – Belém e pousou em alguma das capitais
brasileiras. Ao desembarcar, Carlos fez uma conexão e embarcou em um avião AIII, que seguiu a direção
que forma um ângulo reto, no sentido anti-horário, com a direção seguida pelo avião AII ao partir de
Brasília-DF. Considerando que a direção seguida por um avião é sempre dada pela semirreta com origem
na cidade de partida e que passa pela cidade destino do avião, pela descrição dada, o passageiro Carlos
fez uma conexão em
a) Belo Horizonte, e em seguida embarcou para Curitiba.
b) Belo Horizonte, e em seguida embarcou para Salvador.
c) Boa Vista, e em seguida embarcou para Porto Velho.
d) Goiânia, e em seguida embarcou para o Rio de Janeiro.
e) Goiânia, e em seguida embarcou para Manaus.
Questão 9:(Enem 2009) A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2
metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma
altura de 0,8 metro.
A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é
a) 1,16 metros.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.
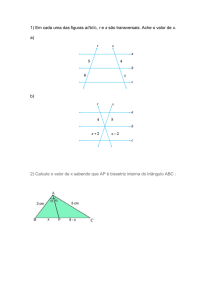
Questão 10: Seja AD uma bissetriz interna do triângulo ABC. Sendo AB = x + 8 , AC = 2x , BD = 10 e
CD = 12 , determine x.
R: 12
Questão 11: Num triângulo ABC , AD é bissetriz interna do ângulo Â. Sabendo-se que BD = 18 , DC
= 27 , AB = (5x - 1) e AC = (7x + 1). Calcule o perímetro do triângulo ABC. R: 105
Questão 12: O perímetro de um triângulo ABC é igual a 45 cm. A bissetriz do ângulo A divide o lado
oposto em dois segmentos, respectivamente iguais a 10 cm e 8 cm. Calcule os lados do triângulo. R:
18 cm ; 15 cm e 12 cm
Questão 13: Os lados de um triângulo, medem 10 ; 15 e 20 m. Calcule a medida do menor dos
segmentos em que a bissetriz interna divide o lado maior. R: 8 m
Questão 14: Um triângulo RST tem os lados medindo RS = 9 cm , ST = 6 cm e TR = 4 cm . Determine
as medidas dos segmentos determinados no lado maior, pela bissetriz do ângulo oposto. R: 3,6 cm e
5,4 cm
Questão 15: A razão de semelhança de dois triângulos eqüiláteros é 2/5. O lado do menor mede 8
m. Calcule a medida do lado do outro triângulo. R: 20 m
Questão 16: Um triângulo, cujos lados medem 12 m, 18 m e 20 m, é semelhante a outro cujo
perímetro mede 10 m. Calcule a medida dos lados do triângulo menor.
R: 2,4 m , 3,6 m e 4 m
Questão 17: Um bambu de 32 côvados, erguendo-se verticalmente sobre o terreno horizontal, é
quebrado num certo ponto pela força do vento. Sua extremidade vem tocar a terra a 16 côvados do seu
pé. A quantos côvados do pé ele se quebrou?
R: 12 côvados
Questão 18: A hipotenusa de um triângulo retângulo mede 40 cm e a razão entre os catetos é de ¾ .
Calcule as medidas dos catetos.
R: 24 cm e 32 cm
Questão 19: Um gavião está no alto de uma árvore vertical de 6 m de altura, ao pé da qual fica a toca
de uma cobra, que se encontra a 18 m da toca. A cobra também vê o gavião, e corre para a toca. O
gavião faz um vôo em linha reta e alcança a cobra antes que ela atinja a toca. Sabendo-se que o gavião
voou a mesma distância percorrida pela cobra, diga a quantos metros da toca a cobra foi alcançada.
R: 8 m