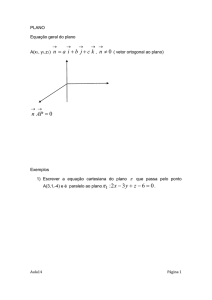
1) O litotriptor é formado pela rotação de uma elipse do eixo menor em volta do eixo
maior. Se um ultra-som é colocado em um dos focos da elipse e um cálculo renal é
colocado no outro foco, então todas as ondas de som emitidas pelo litotriptor atingirão o
cálculo renal. Qual a distância entre o cálculo renal e o ponto V? Dar a resposta com uma
casa decimal.
(valor 1,0)
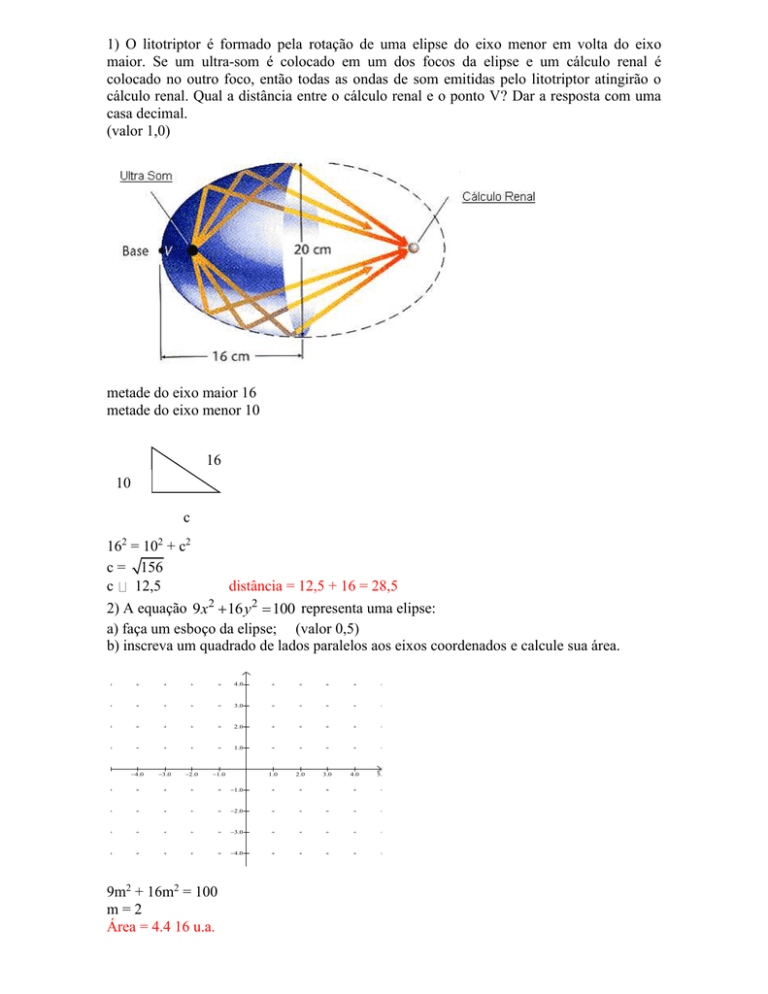
metade do eixo maior 16
metade do eixo menor 10
16
10
c
162 = 102 + c2
c = 156
c 12,5
distância = 12,5 + 16 = 28,5
2
2) A equação 9 x 16 y 2 100 representa uma elipse:
a) faça um esboço da elipse; (valor 0,5)
b) inscreva um quadrado de lados paralelos aos eixos coordenados e calcule sua área.
9m2 + 16m2 = 100
m=2
Área = 4.4 16 u.a.
3) Determine qual dos subconjuntos seguintes de R2 são subespaços. (valor 1,0)
OBS. Não pode haver rasura
(a) ( ) Sim ( X )Não
(b) ( X ) Sim ( )Não
(c) ( ) Sim ( X )Não
(d) ( ) Sim ( X )Não
4) Seja P1 o espaço vetorial dos polinômios de grau 1. Definimos o produto interno entre
p(t ) at b
dois vetores p e q de P1 como segue: p.q 2ac ad bc 2bd , sendo
q(t ) ct d
Calcular o ângulo entre t 1 e 3t .
(valor 1,5)
p.q = 2.1.3 + 1.0 + (-1).3 + 2.(-1).0 = 6 + 0 – 3 + 0 = 3
p
p. p 2.1.1 1.(1) (1).1 2.(1).(1) 2
q q.q 2.3.3 3.0 0.3 2.0.0 18 3 2
cos
3
1
1
cos arccos 60o
2
2
2.3 2
= 60o
5) A figura abaixo representa uma transformação. Para T ser linear devem ser satisfeitas as
condições abaixo. Verifique se T é linear (valor 1,0)
(a0, a1, a2, a3)
a) T(u+v) = T(u) + T(v)
u = ao + a1t + a2t2 + a3t3 v = bo + b1t + b2t2 + b3t3
T(u+v) = T (ao + bo + (a1 + b1)t + (a2 + b2)t2 + (a3 + b3)t3) = (ao + bo, a1 + b1, a2 + b2, a3 + b3)
T(u) + T(v) = (ao , a1 , a2 , a3) + (bo , b1 , b2 , b3) = (ao + bo, a1 + b1, a2 + b2, a3 + b3)
b) T( u) = T(u)
T( u) = T( (ao + a1t + a2t2 + a3t3 )) = T( ao + (a1t) + (a2t2) + (a3t3)) =
( ao , a1, a2, a3)
T(u) = (ao , a1 , a2 , a3) = ( ao , a1, a2, a3)
Sim, T é linear
6) Suponha que as transformações lineares T1: P2 P2 e T2 : P2 P3 são dadas pelas
fórmulas T1(p(x)) = p(x+1) e T2(p(x)) = xp(x). Encontre (T2
T1) (a0 + a1x + a2x2)
(valor 1,0)
(T2 T1) (a0 + a1x + a2x2)= T2(T1 (a0 + a1x + a2x2)) = T2(a0 + a1(x+1) + a2(x+1)2) =
x . (a0 + a1(x+1) + a2(x+1)2) = (a0 + a1 + a2) x+ (a1 + 2a2)x2 + a2 x3
7) Seja T: R4 R3 a transformação linear dada pela fórmula:
T(x,y,z,w) = (4x + y – 2z - 3w, 2x + y + z – 4w, 6x – 9z + 9w). Pedem-se
a) uma base e a dimensão de N(T).
(valor 0,75)
4 x y 2 z 3w 0
2 x y z 4w 0
6 x
9 z 9w 0
2 x y z 4 w 0
4 x y 2 z 3w 0
6 x
9 z 9w 0
2 x y z 4 w 0
y 4 z 5w 0
3 y 12 z 21w 0
2 x y z 4 w 0
y 4 z 5w 0
6w 0
w = 0 , y = -4z e x =
base de N(T) = {(
3
3
z N(T) = { (x, y, z, w) / x = z , y = -4z e w = 0}
2
2
3
, -4, 1, 0)}
2
dimN(T) = 1
b) uma base e a dimensão da Im(T)
(valor 0,75)
x(4,2,6) + y(1,1,0) + z(-2,1,-9) + w(-3,-4,9)
1 1 0 1 1 0 1 1
4 2 6 0 2 6 0 1
2 1 9 0 3 9 0 1
3 4 9 0 1 9 0 0
0
3
9
0
1 1 0
0 1 3
0 0 6
base Im(T)= { (1,1,0), (0, -1, 3), (0,0,1)} dimIm(T) = 3
8) O Gato Arnold sofreu algumas transformações lineares do plano ladrilhado tendo como
transformação final a lei, T(x,y) = ( x + y, x + 2y). A cada transformação do gato Arnold
o(s) autovalor(es) justificam o(s) movimento(s) do(s) autovetor(es).Ache o(s) autovalor(es),
o(s) autovetor(es) associado(s) e identifique o(s) movimento(s) adequadamente. (valor 1,5)
T(x,y) = (x,y)
(x+y, x+2y) = ( x, y)
x+y= x
x + 2y = y
1
1
x- x +y=0
x + 2y - y = 0
1
0 (1 ).(2 ) 1 0
2
2 3 1 0
1 2,6
dilatação na direção do vetor
2 0, 4
contração na direção do vetor
(1 - )x + y = 0
x + (2 - )y = 0