Baixar o arquivo

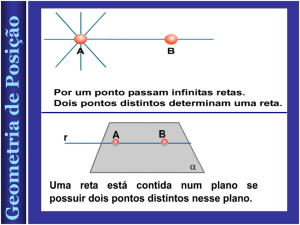
PLANO
Equação geral do plano

A(x1, y1,z1)

n  a i b

 
jc k , n 
0
( vetor ortogonal ao plano)
 
n AP  0
Exemplos
1) Escrever a equação cartesiana do plano  que passa pelo ponto
A(3,1,-4) e é paralelo ao plano  1 : 2 x  3 y
Aula14
 z  6  0.
Página 1
2)Determinar a equação geral do plano que passa pelo ponto A(2,1,-2) e é
 x  4  3t

perpendicular à reta r :  y  1  2t
z  t

Ângulos entre dois planos
Sejam
os
 : a1x  b1 y  c1z  d1  0
planos
 : a2 x  b2 y  c2 z  d2  0

O ângulo entre os planos é o ângulo entre os vetores n 1 e
e

n2
 
cos  
n1 . n2


| n1 | . | n2 |
Aula14
, com
0  cos 

2
Página 2
Exemplos:
1) Determinar o ângulo entre os planos
 2 : 3x  2 y  5 z  4  0 .
1 : 2 x  3 y  5z  8  0
e
Condição de paralelismo
Sejam
os
1 : a1x  b1 y  c1z  d1  0
planos
 2 : a2 x  b2 y  c2 z  d2  0

e

 1 paralelo a  2 se n 1 e n 2 são paralelos
a1 b1 c1
 
a2 b2 c2
Condição de perpendicularismo
Sejam
os
1 : a1x  b1 y  c1z  d1  0
planos
 2 : a2 x  b2 y  c2 z  d2  0

e

 1 perpendicular a  2 se n 1 e n 2 são ortogonais
 
n1 . n 2  0
Aula14
Página 3
Exemplos:
1) Calcular
os
valores
de
m
1 : (2m  1) x  2 y  2 z  3  0
para
e
que
o
plano
 2 :4 x  4 y  4 z  0
sejam paralelos
Aula14
Página 4