Anexo 4ª aula: Conectivos Interproposicionais Os - Fafich

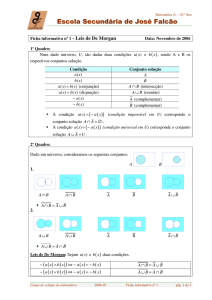
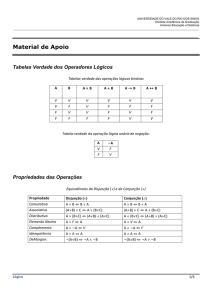
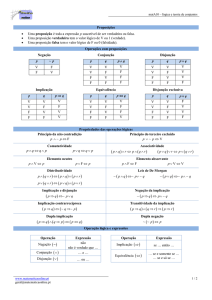
Anexo 4ª aula:
Conectivos Interproposicionais
Os argumentos formulados em uma língua natural são, com freqüência, de difícil
avaliação por causa da natureza vaga e equívoca desta linguagem. Mesmo quando esta
dificuldade é superada, subsiste o problema de determinar a validade ou invalidade dos
argumentos. Para evitar tais inconvenientes, faz-se necessário criar uma linguagem simbólica
artificial, livre desses defeitos, na qual possam ser expressos os argumentos da linguagem
natural. Portanto, os símbolos da lógica moderna ajudam-nos a expor as estruturas de
proposições e argumentos, cujas formas podem ser obscurecidas pela pouca maleabilidade da
linguagem corrente.
Vejamos, agora, os principais símbolos do cálculo proposicional.
1. Variáveis Proposicionais: Letras latinas minúsculas p,q,r,s,.... para indicar as proposições (ou
fórmulas atômicas).
Exemplo:
A lua é quadrada : p
A neve é branca : q

Conectivos Lógicos: As fórmulas atômicas (ou as proposições) podem ser combinadas entre si
e, formando as fórmulas moleculares (ou as proposições compostas). Para representar tais
combinações, usaremos os seguintes conectivos lógicos:
~ (negação): não,
& (conjunção): e,
w e v (disjunção exclusiva e inclusiva): ou,
=> (condicional): se...então,
Exemplos:
A lua não é quadrada. : ~p
A lua é quadrada e a neve é branca. : p & q (p e q são chamados conjunctos)
A lua é quadrada ou a neve é branca. : p v q (p e q são chamados disjunctos)
Se a lua é quadrada, então a neve é branca. : p => q (p é o antecedente e q o conseqüente)
A lua é quadrada se e somente se a neve é branca. : p <=> q
Símbolos Auxiliares: ( ), parênteses servem para denotar o "alcance" dos conectivos.
Exemplos:
Se a lua é quadrada e a neve é branca, então a lua não é quadrada. : ((p & q) => ~p)
A lua não é quadrada se e somente se a neve é branca: ((~ p) <=> q))
4. Tabelas de Verdade
A lógica clássica é governada por três princípios (entre outros) que podem ser formulados
como segue:
a. Princípio da Identidade: Todo objeto é idêntico a si mesmo.
b. Princípio da Contradição: Dadas duas proposições contraditórias (uma é negação da
outra), uma delas é falsa.
c. Princípio do Terceiro Excluído: Dadas duas proposições contraditórias, uma delas é
verdadeira.
Com base nesses princípios as proposições simples (atômicas) são ou verdadeiras ou falsas,
sendo mutuamente exclusivos os dois casos; daí dizer que a lógica clássica é bivalente. Para
determinar o valor (verdade ou falsidade) das proposições compostas (moleculares), como é caso
da negação, da conjunção, da disjunção, da condicional e da equivalência, usaremos tabelasverdade.
4.1. Tabela verdade da "negação": Troca o valor verdade da proposição de partida.
Suponhamos que estivéssemos diante da seguinte proposição ‘João não lê’. Poderemos
interpretar a palavra ‘não’ como a negação do fato de João estar lendo. Isto significa que
podemos considerar João lê como a proposição primitiva, à qual foi aplicado o operador de
negação. Nesse sentido, se João lê, é falso que ele não esteja lendo, assim como se João não lê, é
verdade que ele não esteja lendo.
Representando uma proposição qualquer por uma variável ‘p’ e sua negação por ‘~p’,
bem como verdadeiro e falso por V e F, respectivamente, obtemos a seguinte tabela de valores
verdade para a negação.
p ~p
V F
F V
Não podemos esquecer de que essa simples operação representada por um único símbolo
‘~’ é realizada de muitas maneiras diferentes em nossa linguagem cotidiana. Eis aqui algumas
expressões equivalentes em sua função de negação:
João não lê.
Não é verdade que João lê.
Não ocorre que João leia.
Não se dá o fato de que João leia.
4.2. Tabela verdade da "conjunção": A conjunção é verdadeira se e somente os conjunctos são
verdadeiros.
Suponhamos que estivéssemos diante das seguintes proposições ‘João lê’ e ‘Pedro ri’. A
primeira pode ser verdadeira ou falsa. A segunda também. O que acontece, porém, com a
conjunção de ambas, João lê e Pedro ri. Para afirmarmos que João lê e Pedro ri, é necessário que
os dois fatos ocorram, ou seja, é necessário que os dois fatos ligados pela conjunção ‘e’ sejam
verdadeiros.
Representando ‘e’ por ‘&’, duas proposições por uma variável ‘p’ e outra ‘q’ e mantendo
as convenções para ‘verdadeiro’ e ‘falso’, obtemos a seguinte tabela de valores verdade para a
conjunção:
p
V
V
F
F
q p&q
V
V
F
F
V
V
F
F
Como acontece com o conectivo anterior, a conjunção pode ser expressa de muitas
maneiras na linguagem cotidiana. Eis aqui alguns exemplos:
Apesar de João ler, Pedro ri.
João lê e Pedro ri.
João lê, porém Pedro ri.
Além de João estar lendo, Pedro está rindo.
Não só João lê, como Pedro ri.
Tanto João lê como Pedro ri.
4.3. Tabela verdade da "disjunção exclusiva": A disjunção só é verdadeira quando os disjunctos
possuem valores de verdade diferentes.
Suponhamos que estivéssemos diante da seguinte disjunção ‘Ou João lê e João brinca’.
Esta proposição parece estabelecer um par de alternativas que não podem ser verdadeiros nem
falsas ao mesmo tempo. Se João este lendo neste momento, então ele não está brincando. E se
ele está brincando, então ele não está lendo. Dessa forma, a disjunção, como o próprio nome
indica, exclui uma alternativa em relação à outra.
Mantendo as convenções anteriores e representando a disjunção exclusiva por ‘w’,
obtemos a seguinte tabela geral de verdade.
p
V
V
F
F
q pwq
V
F
F
V
V
V
F
F
Há muitas maneiras de expressar a disjunção exclusiva em português. Utilizando as
proposições do exemplo, podemos ilustrar algumas delas como se segue:
Ou João lê, ou João brinca.
Quer João leia, quer João brinque.
Seja que João leia, seja que ele brinque.
4.4. Tabela verdade da "disjunção inclusiva": A disjunção é falsa se, e somente, os disjunctos
são falsos.
A palavra ‘ou’ pode ser tomada no sentido não exclusivo ou inclusivo. Por exemplo, a
disjunção Paulo vai a pé ou Paulo vai de ônibus. Não estamos necessariamente excluindo uma
das alternativas em relação à outra. Podemos estar afirmando que Paulo, em alguns momentos,
faz determinado trajeto a pé, em outros, o faz de ônibus e, em outros, por fim, faz parte do trajeto
a pé e parte, de ônibus. Nesse caso, estabelecemos uma nova forma de disjunção que aceita
também a verdade das duas alternativas.
Mantendo as convenções anteriores e representando a disjunção inclusiva por ‘v’,
obtemos a seguinte tabela geral de verdade.
p
V
V
F
F
q pvq
V
V
F
V
V
V
F
F
Neste caso, também há muitas maneiras de expressar a disjunção exclusiva em português.
Utilizando as proposições do exemplo, podemos ilustrar algumas delas como se segue:
Ou Paulo vai a pé ou Paulo vai de ônibus.
Quer João leia, quer João brinque.
Seja que João leia, seja que ele brinque.
É importante observar que, ao lidar com a disjunção, toda atenção é pouca, pois as
mesmas expressões do português podem ser empregadas para designar uma ou outra. Portanto, é
tarefa do leitor perceber qual das disjunções está sendo utilizada.
Referência Bibliográfica:
ABAR, Celina. Noções de Lógica Matemática. [online] Disponível na internet via
WWW. URL: http://pucsp.br/~logica Arquivo capturado em 01 de dezembro de 2007.
MARGUTTI PINTO, Paulo Roberto. As Principais Conectivas Intersentencias. In:
Introdução à Lógica Simbólica. Belo Horizonte: Editora UFMG, 2001, p.49-81.