2ª LISTA DE EXERCÍCIOS DE FÍSICA I CAPÍTULO III

2ª LISTA DE EXERCÍCIOS DE FÍSICA I
CAPÍTULO III – MOVIMENTO EM DUAS E EM TRÊS DIMENSÕES
SUGESTÕES PARA O DESENVOLVIMENTO
ATENÇÃO: O objetivo deste arquivo é fornecer pistas para a solução de questões e problemas. Não são soluções
únicas e nem isentas de correções.
1 - Os vetores devem ser paralelos para alcançar um resultante de 7 m de comprimento (o primeiro caso mostrado abaixo vetores A e
B), antiparalelos (em sentidos opostos) para alcançar uma resultante de 1 m de comprimento (segundo caso apresentado vetores A’ e
= 5 m de comprimento (último caso apresentado vetores A’’ e B’’).
B’), e perpendiculares para alcançar um resultante de
Em cada esboço, os vetores
são mostrados em umesboço, mas a resultante não é mostrada. A resultante seria uma reta
traçada do começo ao fim, o início é indicado por A e o final é indicado por B.
2 - Um esboço dos deslocamentos é mostrado. A resultante (não mostrada) seria uma linha reta a partir do início Banco), para terminar
em Walpole. Com um cuidadoso desenho, você deve encontrar que o vetor resultante tem comprimento 29,5 km a 35° oeste (west) do
sul (south).
3 - A componente de x é dada por ax = 7,3 cos 250° = - 2,5 e a componente y é dada por ay = 7,3 sen 250° = - 6,9. Ao considerar a
variedade de maneiras para calcular estes, podemos constatar que o vetor está -70° abaixo do eixo, de modo que as componentes
também poderia ter sido encontrada a partir de ax = 7,3 cos – 70° e
ay = 7,3 sen – 70°.
4 – (a) ⏐v⏐=
= 47,2 m
(b) Lembrando que tan (θ) = tan (θ + 180°), constatamos que as duas possibilidades para tan–1 (40 / - 25)
são −58° e −122°. Notando que o vetor está no terceiro quadrante (pelos sinais das suas componentes x e y), vemos que 122° é a
resposta correta.
5 - Embora pensamos nisto como um movimento tridimensional, ele pode ser efetivamente resolvido bidimensionalmente definindo os
eixos no plano da falha.
(a) A magnitude do deslocamento é
= 27,8 m.
(b) A magnitude da componente vertical de AB é | AD | sem 52° = 13,4 m.
6 - O diagrama mostra os vetores deslocamento para os dois segmentos da sua caminhada, indicados pelos vetores A e B, e o vetor
deslocamento total ( "final"), indicados pelo vetor r. Tomamos a direção leste como a direção + x e a direção norte como a direção + y.
Nós observamos que o ângulo entre A e o eixo x é de 60◦. Sempre que as unidades não são
explicitamente demonstradas, as distâncias são entendidas para estar em metros. Assim, os
componentes de A são Ax = 250 cos 60° = 125 e Ay = 250 sin 30° = 216,5. As componentes de
B são Bx = 175 e By = 0. As componentes do deslocamentos total são rx = Ax + Bx = 125 + 175
= 300 e ry = Ay + By = 216,5 + 0 = 216,5.
(a) A magnitude do deslocamento é resultante
(b) O ângulo resultante que o deslocamento faz com o eixo +x é
(c) A distância total percorrida é d = 250 + 175 = 425 m.
(d) O valor total da distância percorrida é maior do que a magnitude do deslocamento resultante. O diagrama
mostra porque: A e B não são colineares.
7 - Nós escrevemos r = a + b. Quando não expressamente indicadas, as unidades estão aqui a ser assumida metros. Então rx = ax + bx =
4,0 − 13 = − 9,0 e ry = ay + by = 3,0 + 7,0 = 10. Assim, r = (− 9,0 m) î + (10 m) ĵ. A
magnitude da resultante é
O ângulo entre a resultante e o eixo +x é dada por tan−1 (ry / rx) = tan−1 [10 / (− 9,0)] que é ou − 48° ou 132°. Dado que a componente x
da resultante é negativa e y o componente é positiva, características do segundo quadrante, o ângulo correto é 132° (medido a partir de
+ x).
8 - Os vetores são mostrados no diagrama. O eixo x é definido a partir de oeste a leste e o eixo y de sul para norte. Então ax = 5,0m, ay =
0, bx = − (4,0) sin 35 ◦ = −2,29 m, e by = (4,0) cos 35◦ = 3,28m.
(a) Tomando c = a + b. Então cx = ax + bx = 5,0 m − 2,29m = 2,71m e cy = ay + by = 0 +
3,28 m = 3.28m.
A magnitude de c é
(b) O ângulo θ que c faz com o eixo x é:
(c) O vetor b − a é encontrado através da adição de −a com b. O resultado é apresentado
no diagrama abaixo.
Tomando c = b − a. Então cx = bx − ax = − 2,29m − 5,0m = − 7,29m e cy = by - ay = 3.28m. A magnitude
de c é
= 8.0m.
(d) A tangente do ângulo θ que c faz com o eixo + x (leste) é
Há duas soluções: − 24,2° e 155,8°. Como o diagrama mostra, a segunda solução é a correta.
O vetor c = b − a está a 24° a norte do oeste.
9 - Todas as distâncias nesta solução, entendem-se em metros.
(a)
(b)
(c) Tomando a − b + c = 0 temos que c = b + a, o que podemos constatar é o contrário daquilo que encontramos
em (b). Assim,
.
10 - Deve-se mencionar que uma forma eficiente de trabalhar além deste problema é com a lei geral dos cossenos para triângulos (e uma
vez que a, b e r formam um triângulo isósceles, os ângulos são fáceis de encontrar).
No entanto, no interesse de reforçar a habitual abordagem sistemática para a adição vetorial, verificamos que
o ângulo que b faz com o eixo + x é 135° e aplicamos as equações da decomposição vetorial.
(a) A componente x de r é 10 cos 30° + 10 cos 135° = 1,59 m.
(b) A componente y de r é 10 sem 30° + 10 sem 135° = 12,1 m.
(c) A magnitude de r é
(d) O ângulo entre r e a + x direção é tan−1 (12,1/1,59) = 82,5°.
11 - Se quisermos utilizar as equações da decomposição vetorial diretamente, devemos notar que os ângulos de Q, R e S são 100°, 250°
e 310°, respectivamente, se forem medidos no sentido anti-horário a partir do eixo +x.
(a) Usando notação de vetor unitário, com a unidade metro subentendida, temos
P = 10 cos (25°) î + 10 sen (25°)ĵ
Q = 12 cos (100°) î + 12 sen (100°)ĵ R
S = 8,0 cos (250°) î + 8,0 sen (250°)ĵ
P + Q + R + S = P = 10 î + 1,6 ĵ
(b) A magnitude do vetor soma é
anti-horário.
= 10,2 m e seu ângulo é tan−1 (1,6/10) ≈ 9,2° medido a partir do eixo +x no sentido
12 – a) vx é constante em (2), vy é constante em (4) e a é constante em (4)
b) -2 em m/s2 e 3 em m/s.
13 - a, b, c
14 - (a) todos possuem o mesmo módulo; (b) 1 e 2 empatam (o foguete é lançado para cima), depois 3 e 4 empatam (ele é lançado para
dentro do chão!)
15 - (a) 3,2,1; (b) 1,2,3; (c) todos possuem o mesmo módulo; (d) 6, 5,4
16 - (a) menor; (b) não pode ser respondida; (c) igual; (d) não pode ser respondida
17 - (a) 2; (b) 3; (c) 1; (d) 2; e) 3; (f) 1
18 - (a) sim; (b) não; (c) sim
19 - Quando a unidade comprimento não é especificado (nesta solução), a unidade metro deve ser entendida.
(a) O vetor posição, segundo é: r = −5,0 î + 8,0ĵ (em metros).
(b) A magnitude é
(c) Notando que o vetor encontra-se no plano xy, estamos usamos:
onde escolhemos esta possibilidade (122° medido à esquerda da direção + x), uma vez que os sinais dos componentes implica o vetor
está no segundo quadrante.
(d) No interesse de economizar espaço, omitimos o esboço. O vetor está a 32° no sentido anti-horário a partir da
direção + y, onde a direção + y é assumida para ser (como é normal) 90° no sentido anti-horário a partir de + x.
(e) O deslocamento é ∆r = r’− r, onde r é dada na parte (a) e r’ = 3,0 î. Portanto, ∆r = 8,0î – 8,0ĵ (em metros).
(f) A magnitude do deslocamento é
(g) O ângulo do deslocamento, encontra-se a partir de
onde podemos escolher a antiga possibilidade (−45 ◦, o que significa 45 ◦ medidos no sentido horário a partir de + x, ou 315º no sentido
anti-horário a partir de + x), uma vez que os sinais das componentes implicam que o vetor está no quarto quadrante.
20 - (a) Com r1 sendo o vetor posição inicial e r2 como o vetor posição final, temos:
para o deslocamento na notação de vetor unitário (em metros).
(b) Uma vez que não existe componente z, o vetor deslocamento está no plano xy.
21 - O deslocamento total do ∆r é a soma de três deslocamentos, cada um sendo resultado de uma velocidade (constante) durante um
determinado tempo. Nós usamos um sistema de coordenadas com + x a leste e + y a Norte. Na notação de vetor unitário, o primeiro
deslocamento é dado por
em quilômetros. O segundo deslocamento tem uma amplitude de
está a 40° norte do leste. Portanto,
, e a sua direção
em quilômetros.
E o terceiro deslocamento é
em quilômetros.
O deslocamento total é
O tempo da viagem é de 40 + 20 + 50 = 110 min, o que equivale a 1,83 h. Da definição do vetor velocidade média, em seguida, temos:
vM =
em quilômetros por hora. Se deseja-se expressar isso em notação de magnitude e de ângulo, então isto é equivalente a um vetor de
magnitude
, que é inclinada 67,5° norte a partir do leste (ou, 22,5° a leste do norte).
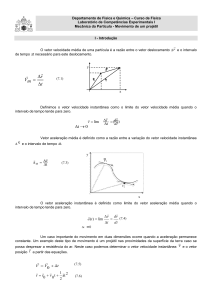
22 - Para enfatizar o fato de que a velocidade é uma função do tempo, adotamos a notação v (t) para dx/dt.
(a) Da definição de vetor velocidade instantânea, temos que
em metros por segundo.
(b) obtendo o resultado em t = 2 s, temos v = (3,0î − 16,0 ĵ )m / s.
.
(c) A velocidade escalar em t = 2 s é
(d) e o ângulo de v nesse momento é uma das possibilidades:
e escolhemos a primeira possibilidade (−79,4° medidos no sentido horário a partir da direção
+ x, ou 281° no sentido anti-horário a partir de + x), uma vez que os sinais das componentes implica o vetor está no quarto quadrante.
23 - (a) Tomando a derivada do vetor posição em relação ao tempo, temos
em unidades SI (m/s).
em unidades SI (m/s2).
(b) Tomando outra derivado em relação ao tempo, temos
24 – (a) usando a expressão dada, obtemos:
em metros.
(b) Tomando a derivada da expressão dada temos
onde escrevemos v (t) para enfatizar a sua dependência do tempo. Isto torna-se, em t = 2,00 s, v = (19,0î − 224ĵ) m/s.
(c) Diferenciar a v (t) encontrada anteriormente, com relção ao tempo, produz 12,0t î − 84,0t2 ĵ, que produz a =
(24,0 î − 336 ĵ) m/s2 em t = 2,00 s.
ou 94,8°,
(d) O ângulo de v, medido a partir + x, é
onde nós ficamos com a primeira escolha (−85 ,2°, que é equivalente a 275°), uma vez que os sinais de suas
componentes implicam que ele está no quarto quadrante.
25 - A aceleração constante em ambas as direções (x, y) nos permite as equações do M.R.U.V. para o movimento ao longo de cada
direção. Isto pode ser tratado individualmente (para ∆x e ∆y) ou juntamente com a notação de vetor unitário (para um ∆r). Quando as
unidades não são indicadas, unidades SI devem ser subentendidas.
a) A velocidade da partícula em qualquer momento t é dado por v = v0 + at, onde v0 é a velocidade inicial
e a é a aceleração (constante). A componente é x = vx v0x + axt = 3,00 − 1,00t, e a componente y é vy = v0y + ayt = −0,500t uma vez que
v0y = 0. Quando a partícula atinge a sua coordenada x máxima em t = tm, temos de ter vx = 0. Portanto, 3,00 − 1,00tm = 0 ou tm = 3,00 s.
A componente y da velocidade neste momento é vy = − 0,500t (3,00) = −1,50 m/s; esta é a única componente não-nula de v em t = tm.
b) Como o movimento começou na origem, as coordenadas da partícula, a qualquer momento, são dadas por r = v0t+1/2 at2. Em t = tm
temos:
em metros.
26 - Como as componentes x e y da aceleração são constantes, então nós podemos utilizar as equações do M.R.U.V. para o movimento
em ambos os eixos. Isto pode ser tratado individualmente (para ∆x e ∆y) ou juntamente com a notação de vetor unitário (para um ∆r).
Quando as unidades não são indicadas, unidades SI devem ser subentendidas.
a) Como r0 = 0, o vetor posição da partícula é:
Assim, encontramos quando x = 29 m, resolvendo 2,0t2 = 29, o que leva a t = 3,8 s. A coordenada y
nesse momento é y = 8,0 (3,8) + 1,0 (3,8)2 = 45 m.
(b) a velocidade das partículas é dada por
Assim, em t = 3,8 s, a velocidade é
que tem um módulo de:
27 - Adotamos o sentido positivo tal como utilizado normalmente, de modo que as equações do M.R.U.V. são
diretamente aplicáveis.
a) Com a origem no ponto de disparo, a coordenada do ponto y da bala é dada por y = −gt2/2. Se t é o
tempo de vôo e y = −0,019 m indica que a bala atinge o alvo, então:
b) A velocidade do disparo é a velocidade inicial (horizontal) da bala. Dado que x = 30 m é a posição horizontal
do alvo, temos x = v0t. Deste modo,
28 - Adotamos o sentido positivo tal como utilizado normalmente, de modo que as equações do M.R.U.V. são
diretamente aplicáveis. A velocidade inicial é horizontal, assim v0y = 0 e v0x = v0 = 161 km/h.
Convertendo para unidades SI, temos v0 = 44,7 m/s.
(a) Com origem no ponto inicial (onde a bola deixa a mão do lançador), a coordenada y da bola é dada por y = −gt2/2, e a coordenada x
é dada por x = v0t. Desta última equação, temos um simples proporcionalidade entre a distância horizontal e o tempo, o que significa
que o tempo para viajar a metade da distância total é a metade do tempo total. Especificamente, se x = 18,3 ÷ 2 = 9,15 m, então t =
(9,15) / 44,7 = 0,205 s.
b) E o tempo de viagem para os próximos 9,15 m deve ser também 0,205 s. Pode ser útil escrever a
equação horizontal como ∆x = v0∆t, a fim de que este resultado pode ser visto de forma mais clara.
c) De y = −gt2/2, vemos que a bola atingiu a altura de −(9,8) (0,205)2/2 = −0,205 m no momento em que a bola está a meio caminho para
o batedor.
d) A altura da bola quando ela atinge o batedor for −(9,8) (0,409)2/2 = −0,820m, o qual, quando subtraídos
a partir do resultado anterior, implica que a bola caiu mais 0,615 m. Uma vez que o valor de y não é simplesmente proporcional a t, não
se espera que os intervalos de tempo iguais correspondam à igualdade na mudança da altura, num sentido físico, isto é devido ao fato de
que a velocidade inicial y para a primeira metade do movimento não é a mesmo que a velocidade inicial y para a segunda metade do
movimento.
29 - Uma vez que esse problema implica uma aceleração constante descendente de magnitude a, semelhante à situação do movimento
do projétil, usamos as equações do M.R.U.V., enquanto que a substitui g. A velocidade inicial é horizontal, de modo que v0y = 0 e v0x =
v0 = 1,0 x 109 cm/s.
a) Se l é o comprimento de uma placa e t é o tempo que um elétron está entre as placas, então l = v0t, onde
v0 é a velocidade inicial. Deste modo
b) O deslocamento vertical do elétron é
c) e (d) A componente x da velocidade não muda: vx = v0 = 1,0 x 109 cm / s, e a componente y é
30 - A origem está no ponto de lançamento (a posição inicial da pedra). A componente x
da sua velocidade inicial é dada por v0x = v0 cos θ, e a componente y é dada por v0y = v0 senθ, onde v0 = 20 m/s é a velocidade inicial e
θ = 40,0° é o ângulo de lançamento.
a) Em t = 1,10 s, a sua coordenada x é
b) Neste instante a sua coordenada y é
1
c) Em t’ = 1,80 s, a sua coordenada x é
d) Neste instante a sua coordenada y é
e) e (f) A pedra atinge o solo antes de t = 5,0 s. Para encontrar o momento em que atinge o solo
resolver
para t. Achamos
Sua coordenada x é na aterrissagem é:
.
Assumindo que permanece onde ela cai, as suas coordenadas em t = 5,00 s são:
x = 40,2m e y = 0.
31 - A origem é coordenar, no final do cano do rifle (o ponto inicial em que começa o movimento do projétil), e deixamos θ0 ser o
ângulo do disparo. Se o alvo está afastado a uma distância d, as respectivas coordenadas finais são x = d, y = 0. O movimento do
projétil leva às equações d = v0t cosθ0 e 0 = v0t senθ0 − gt2/2. Eliminando t, temos 2v02senθ0cosθ0 − gd = 0. Usando o pecado senθ0 cos
θ0 = ½ sen(2θ0), obtemos
que produz sen (2θ0) = 2,12 × 10-3 e, consequentemente θ0 = 0,0606°. Se a arma é mirada num ponto a uma
distância l acima do alvo, então tan θ0 = l / d, assim:
32 - Nós designamos a velocidade dada v = 7,6i + 6,1j (em unidades SI) sendo v1 − oposta à velocidade
quando ela atinge a altura máxima v2 ou a velocidade quando ela retorna para a terra v3 − e tomando v0 como a
velocidade de lançamento, como de costume. A origem está no seu ponto de lançamento do solo.
a) Diferentes abordagens são possíveis, mas, uma vez que ela será útil (para o resto do problema), primeiro
encontramos a velocidade inicial em y. Usando a equação de Torricelli, temos:
que gera v0y = 14,7 m/s. Sabendo que v2y deve ser igual a 0, usamos a equação de Torricelli novamente, mas agora com ∆y = h para a
altura máxima:
que gera h = 11 m.
b) Recordando a obtenção da equação do alcance, mas usando v0y para v0 sen θ e v0x para v0 cos θ, temos
.Observando que v0x = v1x =7,6 m/s, nós substituímos os valores e obtemos:
o que conduz a
R = 2 (7,6) (14,7) / 9,8 = 23 m.
c) Como v3 = v1x = 7,6 m/s e v3y= −v0y = −14,7 m/s, temos
d) O ângulo (medido a partir horizontal) para v3 é:
, uma vez que os sinais de suas componentes implicam que ele está no quarto quadrante.
33 - A origem está na coordenada da posição inicial da “bola”, e θ é o ângulo da sua velocidade inicial medido a partir do eixo + x.
a) x = 46m e y = −1,5m são as coordenadas para o ponto de desembarque; ele atinge o chão no momento t = 4,5 s. Desde que x = v0xt,
Uma vez que
GT2
A magnitude da velocidade inicial é
b) O ângulo inicial satisfaz tan θ = v0y/v0x. Assim, θ = tan−1 (21,7/10,2) = 64,8º.
34- Nós denotamos h como a altura de um degrau e w como a largura. Para acertar passo n, a bola deve cair uma distância nh e percorrer
uma distância horizontalmente entre (n −1)w e nw. Tomamos a origem de um sistema de coordenadas para estar no ponto onde a bola
deixa o topo da escada, e podemos escolher o eixo y a ser positivo
no sentido ascendente. As coordenadas da bola no momento t são dadas por x = v0xt e y = −gt2/2 (desde que v0y = 0). Nós igualamos y a
−nh para o tempo para atingir o nível do degrau n:
A coordenada x é então
O método é tentar valores de n até encontrarmos um para o qual x/w é menor do que n mas superior a n − 1. Para
n = 1, x = 0,309m e x/w = 1,52, que é maior do que n. Para n = 2, x = 0,437m e x/w = 2,15, que também é maior do que n. Para n = 3, x
= 0,535m e x/w = 2,64. Agora, este é inferior a n e maior que n − 1, de modo que a bola bate no terceiro degrau.
35 - Nós determinamos a velocidade escalar v para encontrar aceleração a.
a) Uma vez que o raio da Terra é de 6,37 × 106 m, o raio de órbita do satélite é 6,37 × 106 m + 640 × 103 m
= 7,01 × 106 m. Portanto, a velocidade do satélite é
b) A magnitude da aceleração é
36 - Nós aplicar a equação da aceleração centrípeta para determinar a velocidade v e depois encontrar o período T.
a) Obtemos
b) O tempo para completar uma volta (o período) é T = 2π r/v = 1,7s. Portanto, em um minuto (t = 60 s),
o astronauta executa
revoluções.
Assim, 35 rpm são necessárias para produzir uma aceleração centrípeta de 7g quando o raio
é 5,0 m.
c) Como foi assinalado acima, T = 1,7s.
37 - O raio da Terra é de 6,37 × 106 m.
a) A velocidade de uma pessoa no equador é v = 2π R/T, aqui R é o raio da Terra (6,37 × 106 m)
e T é a duração de um dia (8,64 × 104 s): v = 2π (6,37 × 106 m) / (8,64 × 104 s) = 463m / s. A magnitude da aceleração é dada por
.
b) Se T é o período, então v = 2π R/T é a velocidade e a = v2/R = 4π2R2 / T2R = 4π2R/T2 é a magnitude da aceleração. Deste modo
38 - a) Uma vez que a roda completa 5 voltas em 1 minuto, o seu período é um quinto de um minuto, ou 12 s.
b) A magnitude da aceleração centrípeta é dada por a = v2/R, onde R é o raio da roda, e v é a velocidade do passageiro. Uma vez que o
passageiro vai uma distância 2πR para cada volta, sua velocidade é
e sua aceleração centrípeta é
Quando o passageiro encontra-se no ponto mais alto, a sua aceleração centrípeta é descendente, em direção ao
centro da roda.
c) No ponto mais baixo, o vetor aceleração centrípeta aponta para cima, em direção ao centro da roda.
Ela tem a mesma magnitude da parte (b).
39 - Nós aplicar a equação v = 2πr / T para determinar a velocidade v e ac = v2/R para encontrar a aceleração centrípeta
a) v = 2πr / T = 2π (20 km)/1,0 s = 1,3 × 105 km/s.
b)
c) Como é evidente, tanto v como a aumentarão se T é reduzido.
40 - Para calcular a aceleração centrípeta da pedra, precisamos de saber a sua velocidade durante o
movimento circular (esta é também a sua velocidade inicial quando ele voa solto). Usamos as equações de do movimento de projéteis
para encontrar essa velocidade. Tomando o sentido + y para cima e colocamos a
origem no ponto onde a pedra deixa sua órbita circular, em seguida, as coordenadas da pedra durante
seu movimento como um projétil são dadas por x = v0t e y = −gt2/2 (desde que v0y = 0). Ela atinge o solo em
x = 10m, y = −2,0m. Formalmente resolvendo a segunda equação para o tempo, obtemos
que nós substituímos na primeira equação:
Portanto, a magnitude da aceleração centrípeta é
,