Slide 1 - WordPress.com

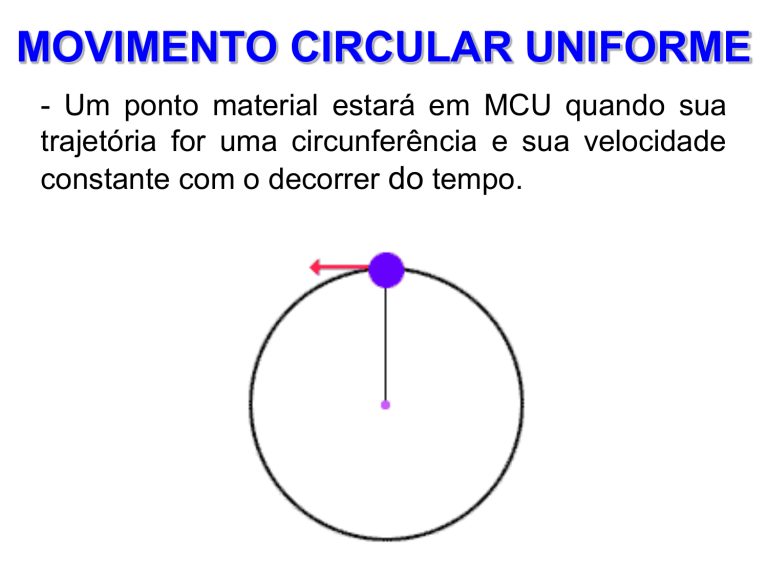
MOVIMENTO CIRCULAR UNIFORME
- Um ponto material estará em MCU quando sua
trajetória for uma circunferência e sua velocidade
constante com o decorrer do tempo.
Vamos considerar o movimento
para uma volta completa.
Frequência e Período
- Frequência é o número de vezes que um
fenômeno se repete num determinado tempo.
- Período é o tempo necessário para o
fenômeno se repetir.
Obs: Para uma volta completa, o móvel deverá percorrer o
perímetro de uma circunferência de raio R em um tempo ,
que denominamos agora como PERÍODO. Definimos
Período(T) o tempo para o móvel completar uma volta numa
circunferência.
1
f 
T
R
1
T
f
Imaginemos nosso carrinho
executando 15 voltas por minuto.
- Podemos dizer então
que a frequência desse
movimento é de 15 ciclos
por minuto ou 15 rotações
por minuto ( 15rpm ).
-Se quisermos achar a frequência em
segundos, basta dividirmos por 60(1min=60s).
15
1
1
15rpm  rps  rps  Hz
60
4
4
Conclusão: O corpo dá uma volta a cada 4
segundos. Quatro segundos então seria o
período do movimento.
Ângulo Horário ou Fase
S: comprimento do arco
ou espaço percorrido

R
S
R: raio
: ângulo em radianos
S

R
Obs: π radianos corresponde a 180º
Velocidade Linear no MCU
No Movimento circular iremos definir todas as
grandezas físicas considerando sempre uma
volta completa.
Se para uma volta completa o tempo seria um
período T então concluímos que:
Para uma volta completa o móvel percorreria o
perímetro da circunferência de raio R dada pela
expressão C = 2πR.
∆t = T e ∆s = 2πr
R

 = 2πrad
A Ξ A0
2R
v
T
Velocidade Angular ( ω )
Podemos
concluir
que,
sempre
no
deslocamento de um móvel ao longo de uma
pista circular, além do deslocamento ao longo
da linha da circunferência,
têm-se um
deslocamento angular ∆ no mesmo intervalo
de tempo ∆t .
P0
P2
t
1
2
P0

P1


t
Lembrando que estamos definindo as grandezas físicas
para uma volta completa, podemos determinar a velocidade
angular do seguinte modo:
-Para uma volta completa, ângulo de fase = 360º, ou 2πrad.
-O tempo para completar uma volta é de um período T.
Conclui-se então que.
 2


t
T
Então se:
2

T
Temos então:
E como:
Teremos:
e
1
f 
T
  2 f
2R
v
T
v  R
ou
v  2Rf
Unidade de velocidade angular
rad

s
Radianos por segundo
Função Horária Angular do MCU
-Função horária no MRU é s = s0+ vt.
-Para localizar um ponto material no MCU
teremos também uma função bem parecida.
Como:
S, t

R
0


t
  0

t 0
S0, t0
Origem
t     0
  0  t
 = 0 +  t
: ângulo ou fase no instante t
0: ângulo inicial ou fase inicial
: velocidade angular
t: tempo
Obs: ( ômega ) é dado em rad/s, já
que o ângulo de fase  é dado em rad.
Acoplamento de Polias
-Com a finalidade de multiplicar forças,
constituindo assim uma máquina simples,
podemos associar rodas e eixos. Duas rodas
acopladas a um mesmo eixo ou duas rodas
acopladas por correia são exemplos de
dispositivos simples capazes de multiplicar
forças.
Aplicação Prática
-Motores em geral tem rotação fixa, mas
esses motores irão acionar máquinas que
possuem sistemas girantes com diferentes
frequências de rotação.
Tipos de acoplamentos
1º Acoplamento por correia:
-Admitindo que a correia seja inextensível,
todos os seus pontos possuem a mesma
velocidade
-Admitindo-se que não haja escorregamento.
Os pontos periféricos de cada polia possuem a
mesma velocidade escalar, que é igual a
velocidade escalar da correia.
v1  v2
2º Acoplamento com mesmo eixo:
-Neste caso A e B descrevem o mesmo ângulo
central no mesmo intervalo de tempo.
-A velocidade angular de um ponto periférico da
polia 1 é igual a velocidade angular de um
ponto periférico da polia 2, isto é:
1  2
B
A