Caderno 12 – Aulas 19 e 20

Professora Bruna
Caderno 12 – Aulas 19 e 20
Período, frequência e velocidade angular.
Página 273
Professora Bruna
Movimentos Periódicos
 Definimos como movimento periódico como qualquer movimento
que se repita.
 O movimento dos ponteiros de um relógio é um exemplo de
movimento periódico, assim como o movimento de rotação da
Terra.
 Outro exemplo comum de um movimento periódico é o
movimento de um pêndulo.
Professora Bruna
Período e Frequência
 Para movimentos periódicos definem-se duas grandezas: o período
e a frequência.
 O período (T) representa o tempo necessário para que o
movimento periódico se repita.
 A frequência é o número de vezes que o movimento periódico se
repete por unidade de tempo.
Professora Bruna
Período e Frequência
 Estas duas grandezas (período e frequência) relacionam-se através
da seguinte expressão:
1
𝑇=
𝑓
𝑜𝑢
1
𝑓=
𝑇
 No SI, a unidade para o período T é o segundo (representa o
tempo necessário para uma oscilação). Já a unidade para a
frequência é 1 𝑠 = 𝑠 −1 , chamada de Hertz e representada por
Hz.
Professora Bruna
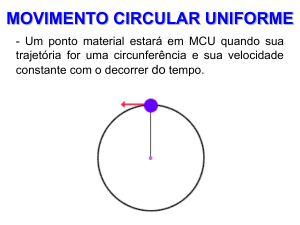
O MCU e a Velocidade Angular
 O movimento circular uniforme (MCU) também é um exemplo
de movimento periódico.
 No MCU a trajetória seguida pelo corpo em movimento é
representada por uma circunferência, de raio r. Temos para este
movimento velocidade constante, que será representada por V.
Professora Bruna
O MCU e a Velocidade Angular
 Neste tipo de movimento, o deslocamento do corpo sempre
corresponde a um arco de circunferência.
 Este arco de circunferência sempre relaciona-se com um
determinado ângulo de abertura.
 Portanto chamaremos o deslocamento de um corpo que realiza
um movimento circular uniforme de deslocamento angular, que
será representado por ∆∅ (delta fi).
Professora Bruna
O MCU e a Velocidade Angular
 A cada deslocamento angular ∆∅ , corresponde um arco de
circunferência de comprimento l.
 O ângulo de um radiano corresponde a um arco de comprimento
igual ao raio da circunferência.
Professora Bruna
O MCU e a Velocidade Angular
 Podemos então determinar uma relação entre o deslocamento
angular e o comprimento de arco, através da seguinte regra de
três:
1 𝑟𝑎𝑑
𝑟
=
∆∅
l
 De onde podemos concluir que:
l = ∆∅ . 𝑟
Professora Bruna
O MCU e a Velocidade Angular
 Definido o deslocamento que um corpo que realiza um MCU
possui, podemos então calcular sua velocidade, já que a velocidade
é dada pela relação entre o deslocamento e o tempo necessário
para o deslocamento:
l
∆∅
=
.𝑟
∆𝑡
∆𝑡
V
𝜔
𝑉 = 𝜔 .𝑟
Professora Bruna
O MCU e a Velocidade Angular
 A relação encontrada corresponde à velocidade do corpo em
MCU, e podemos escrevê-la como:
𝑉 = 𝜔 .𝑟
 Nesta expressão, 𝜔 é a velocidade angular do corpo, já que
representa a variação do deslocamento angular em um
determinado intervalo de tempo. Sendo assim a velocidade
angular é dada por:
∆∅
𝜔=
∆𝑡
Professora Bruna
A relação entre 𝜔, T e f.
 Se considerarmos uma volta completa para o MCU, temos: ∆∅= 2𝜋
rad, e como definimos anteriormente, o tempo necessário para uma
volta (oscilação completa) é o período (T). Desta forma, teríamos
uma velocidade angular dada por:
∆∅
2𝜋
𝜔=
=
∆𝑡
𝑇
Mas como a frequência é o inverso do período, podemos reescrever
esta expressão como:
𝜔 = 2𝜋𝑓
Professora Bruna
Caderno 12 – Aulas 19 e 20
Período, frequência e velocidade angular.
Exercícios de Aula – Página 274
Professora Bruna
Exercícios de Aula
 Exercício 1 – (a)
No MCU, a intensidade da velocidade é constante, portanto a
aceleração tangencial é nula. A aceleração do corpo será dada apenas
pela aceleração centrípeta que pode ser calculada através da seguinte
expressão:
𝑉2
𝛾 = 𝑎𝑐 =
𝑟
Professora Bruna
Exercícios de Aula
 Exercício 1 – (b)
A intensidade da velocidade será dada pela relação entre o
deslocamento l e o tempo gasto para este deslocamento, ou seja:
∆l
𝑉=
∆𝑡
Professora Bruna
Exercícios de Aula
 Exercício 1 – (c)
Por definição, um ângulo de 1 radiano é aquele associado a um arco
de circunferência igual ao raio. Podemos então estabelecer a seguinte
relação:
1 𝑟𝑎𝑑
𝑟
=
∆∅
l
Assim:
l = ∆∅ . 𝑟
Professora Bruna
Exercícios de Aula
 Exercício 1 – (d)
Da relação entre l e ∆∅:
l = ∆∅ . 𝑟
A velocidade do corpo (V) é dada pela relação entre o deslocamento
l e o tempo necessário para este deslocamento. Já a velocidade
angular do corpo (𝜔) é dada pela relação entre o deslocamento
angular do corpo ∆∅ e o tempo necessário para este deslocamento:
l
∆∅
=
.𝑟 =
∆𝑡
∆𝑡
𝑉 = 𝜔 .𝑟
Professora Bruna
Exercícios de Aula
 Exercício 1 – (e)
No MCU, uma volta completa do corpo representa um deslocamento
e o tempo necessário para uma volta completa, como já
definido é representado pelo período T, assim temos:
∆∅ = 2𝜋
∆∅
2𝜋
𝜔=
=
∆𝑡
𝑇
Professora Bruna
Exercícios de Aula
 Exercício – (f)
A frequência representa o número de vezes que completa-se uma
volta (oscilação) em um determinado intervalo de tempo, e é dada
por:
1
𝑓=
𝑇
Assim, a relação entre a velocidade angular e a frequência é
dada por:
∆∅
2𝜋
𝜔=
=
= 2π𝑓
∆𝑡
𝑇
Professora Bruna
Exercícios de Aula
 Exercício 2 –
𝑉=
∆l
∆𝑡
l = ∆∅ . 𝑟
Para o ponto A:
∆∅ = 𝜋 2 𝑟𝑎𝑑
𝑟 =1𝑚
𝜋
𝜋
l = .1 = 𝑚
2
2
Professora Bruna
Exercícios de Aula
 Exercício 1 – (a)
Sendo assim, as velocidades para os pontos A e B serão:
𝜋
𝜋
2
𝑉𝐴 =
= = 0,785 𝑚/𝑠
2
4
𝜋
𝜋
4
𝑉𝐵 =
= = 0,392 𝑚/𝑠
2
8
Professora Bruna
Exercícios de Aula
 Exercício 2 – (a)
Para o ponto B:
∆∅ = 𝜋 2 𝑟𝑎𝑑
𝑟 = 0,5 𝑚
𝜋
𝜋
l = . 0,5 = 𝑚
2
4
Professora Bruna
Exercícios de Aula
 Exercício 2 – (b)
∆∅
𝜔=
∆𝑡
Tanto para o ponto A quanto para o ponto B, os deslocamentos
angulares foram iguais, ou seja:
∆∅ = 𝜋 2 𝑟𝑎𝑑
E o tempo para este deslocamento também foi igual para ambos
os pontos, ou seja, 2 s.
Professora Bruna
Exercícios de Aula
 Exercício 2 – (b)
Portanto, a velocidade angular para ambos os pontos foi igual e
pode ser calculada através da expressão:
𝜋
∆∅
𝜋
2
𝑟𝑎𝑑
𝜔=
=
= 𝑟𝑎𝑑/𝑠
∆𝑡
2𝑠
4
Professora Bruna
Exercícios de Aula
 Exercício 3 – (a)
Considerando o referencial fixo na Terra, o Sol realiza um
movimento circular e uniforme.
Professora Bruna
Exercícios de Aula
 Exercício 3 – (b)
O período corresponde ao tempo necessário para uma volta
completa. Considerando que o Sol realiza o movimento de rotação
em torno da Terra, seu período é de 24 h.
Já a velocidade angular é dada por:
∆∅
𝜔=
∆𝑡
Professora Bruna
Exercícios de Aula
 Exercício 3 – (b)
A unidade solicitada para a velocidade angular neste caso é de graus/hora,
sendo assim, temos que considerar o deslocamento angular da Terra em
graus e o tempo necessário para este deslocamento em horas. Sendo assim:
∆∅ = 360° 𝑒
∆𝑡 = 24ℎ
Sendo assim, a velocidade solicitada será:
360°
𝜔=
= 15°/ℎ
24 ℎ
Professora Bruna
Exercícios de Aula
 Exercício 3 – (c)
Para que a sombra da haste vertical seja projetada às 15 horas, ou
seja, para direita, o Sol deve se movimentar para esquerda (sentido
anti-horário). Como constatado no exercício anterior, o Sol se move
a uma velocidade de 15º/h, portanto, o ele deve se mover 45º para
que o relógio de sol marque 15 horas.
Professora Bruna
Exercícios de Aula
 Exercício 3 – (d)
Dividindo a circunferência em 24 partes iguais (15º cada uma) temos
um relógio enumerado de 0 a 23, números correspondentes às horas
do dia.
Professora Bruna
Exercícios de Aula
 Exercício 3 – (e)
Pelo princípio geral para a construção dos relógios solares é
alinhar o poste do relógio com o eixo de rotação com a Terra.
Dessa forma, para um relógio solar no equador, devemos
colocar o poste em uma direção horizontal, ou seja, paralela a
superfície terrestre.
Professora Bruna
Exercícios de Aula
 Exercício 3 – (f)
A haste vertical deve ser paralela ao eixo de rotação da Terra, mas
deve formar 30º com a superfície da Terra ao Sul.
Professora Bruna
Exercícios de Aula
 Exercício 3 – (g)
A haste vertical do disco deve formar 30º com a direção Sul.