O TIJOLO DE EULER

O TIJOLO DE EULER
Sebastião Vieira do Nascimento
E-mail: [email protected]
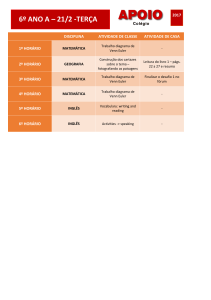
O tijolo de Euler é um paralelepípedo regular de lados que são números
inteiros A, B e C (sendo A>B>C)
cujas diagonais de face, DAB, DAC e
DBC, também são números inteiros.
Se a diagonal principal (que liga os
pontos M e N na figura) também é
um número inteiro, o tijolo é dito
perfeito.
Não se conhece nenhum exemplo de
um tijolo perfeito de Euler
.
O tijolo simples de Euler, imperfeito, com os menores valores para A, B e C
que se conhece tem A = 240, B = 117 e C = 44. As diagonais são: DAB = 267,
DAC = 244 e DBC = 125. Foi descoberto em 1719, pelo matemático Halcke.
Com o advento dos computadores ficou muito mais fácil achar tijolos de
Euler. Ao que parece, já são conhecidos os 5000 menores tijolos, medidos pelo
maior lado. Os 5 primeiros são:
240, 117 e 44; 275, 252 e 240; 693, 480 e 140; 720, 132 e 85; 792, 231 e
160.
O problema matemático relacionado é achar uma ou mais fórmulas que
produzam todos os tijolos perfeitos de Euler que existem. Até hoje ninguém
conseguiu essas fórmulas.
DEDUÇÃO DAS FÓRMULAS QUE PRODUZEM TODOS OS TIJOLOS
EULER
DE
A figura abaixo é um paralelepípedo retângulo, onde são mostradas, respectivamente, a diagonal
da base e a diagonal do paralelepípedo.
Base
E
D
c
A
b
p
c D
b
d
a
B
A
d
a
Secção diagonal
C
E
b
c
B
D
p
d
B
Como os triângulos ABD e DBE são retângulos e, além disso, fazendo coincidir a diagonal
da base com um dos catetos da diagonal do paralelepípedo, obtém-se:
E
c
p
D
d
b
a
B
A
A diagonal (d) da base é tal que d2 = a2 + b2. Para a diagonal (p) do paralelepípedo, temos: p2 = c2 +
+ d2. Portanto, a fim de que os lados, a altura e a diagonal da base do paralelepípedo sejam números
inteiros, basta que os dois ternos (b, a, d) e (d, c, p) sejam pitagóricos.
Já que a diagonal da base é um dos catetos do triângulo retângulo que forma a diagonal do
paralelepípedo, logo, as dimensões de cada tijolo e sua diagonal, em números inteiros, são
dadas pela quadra (b, a, c, p).
Seja b o lado menor do tijolo. Como o triângulo ABD tem que ser pitagórico, logo, d2 = a2 + b2 ou (d
b2
+ a) =
. Uma vez que a e d são inteiros, logo, (d – a) tem que dividir b2 sem deixar resto.
d a
Logo, (d – a) são os divisores positivos de b2. Seja b um primo ímpar. Os divisores de b2 são: b2, b e
b2
2
1. Substituindo b , b e 1 em (d  a) 
, obtém-se os seguintes sistemas de equações:
d a
d – a = b2
S1
d–a=b
S2
d+a = 1
d–a=1
S3
d+a=b
d + a = b2
Dos três sistemas de equações acima, somente o S3 é compatível. Resolvendo o S3, obtém-se:
b2 1
e a=d–1
d
2
d2
Já que p2 = c2 + d2, então, p  c 
. Como b é um primo ímpar, logo, d pode ser um primo ímpar
pc
ou um número composto ímpar.
Se d for um primo ímpar, então, chega-se aos mesmos resultados que se chegou para b, ou seja, três
sistemas de equações, S1, S2 e S3 , dos quais somente o S3 é compatível. E obtém-se para p e c as
seguintes fórmulas:
d 2 1
p
e c=p–1
2
Resposta. Se b e d forem dois primos ímpares, então, só existe um tijolo de Euler.
As medidas das diagonais do tijolo de Euler são dadas por:
d
b2 1
(diagonal da base do tijolo de Euler)
2
p
d 2 1
(diagonal MN do tijolo de Euler)
2
As dimensões do tijolo de Euler são dadas por:
a = d – 1 (lado maior)
b = (lado menor)
c = p – 1 (altura)
Como d 2  a 2  b 2 , então, d  a 
b2
b2
. Se d – a = m, então, d  a 
d a
m
Somando as duas equações membro a membro, obtém-se:
2d 
b2  m2
b2
e a=d – m
 m ou d 
2m
m
b2
b2
 m seja par,
Suponha que b seja par. Como 2d é sempre par, logo, a fim de que a soma
em
m
m
têm que ser ambos pares. Portanto, o número de triângulos pitagóricos é igual ao número de vezes
b
b2
em que m (par) <
dividir b2 sem deixar resto e, além disso,
seja par.
2
m
Se b for um número ímpar composto, então, como 2d é sempre par, logo, a fim de que a soma
b2
 m seja par m tem que ser ímpar. Portanto, o número de triângulos pitagóricos é igual ao
m
número de vezes em que m (ímpar) < b dividir b2 sem deixar resto.
d2
d2
. Se p – c = k, então, p  c 
.
k
pc
Somando as duas equações membro a membro, obtém-se:
Já que p 2  c 2  d 2 , então, p  c 
2p 
d2
 k ou
k
p
d2  k2
e c=p–k
2k
Se d for um número par ou um ímpar não-primo, chega-se às mesmas conclusões que se chegou para
b par ou ímpar, ou seja, se d for par, o número de triângulos pitagóricos é igual ao número de vezes
d
d2
dividir d2 sem deixar resto e, além disso,
seja par. Se d for ímpar composto,
2
k
o número de triângulos pitagóricos é igual ao número de vezes em que k (ímpar) < d dividir d2 sem
deixar resto.
em que k (par) <
As medidas das diagonais do tijolo de Euler são dadas por:
b2  m
2
2
d  k2
p
2k
d
(diagonal da base do tijolo de Euler)
(diagonal MN do tijolo de Euler)
As medidas das dimensões do tijolo de Euler são dadas por:
a = d – m (lado maior)
b = (lado menor)
c = p – k (altura)
Exemplo 1. Se o lado menor de um tijolo for 5, quantos tijolos de Euler existem?
Resolução:
Cálculo da diagonal da base do tijolo de Euler:
d
52  1
= 13
2
Resposta. Como b = 5 e d = 13 são ambos primos, logo, só existe um tijolo de Euler com o lado menor
5
Cálculo da diagonal MN do tijolo de Euler
132  1
= 85
2
Cálculo das dimensões do tijolo de Euler:
p
a = 13 – 1 = 12
b=5
c = 85 – 1 = 84
VERIFICAÇÃO: p  122  52  842  144  25  7056  85
Sejam DAB, DAC e DBC, respectivamente, as diagonais do tijolo de Euler.
D AB  12 2  5 2  13 ,
D AC  12 2  84 2  84,85 e DBC  5 2  84 2  84,15 .
Portanto, se a DMN for inteira, somente a DAB é inteira, ou seja, somente a diagonal da base do tijolo
de Euler é inteira.
Exemplo 2. Se o lado menor de um tijolo for 7, quantos tijolos de Euler existem?
Resolução:
Cálculo da diagonal da base do tijolo de Euler:
72 1
= 25
d
2
Como a diagonal da base, do tijolo de Euler, é um número composto ímpar, logo, o número de tijolos
será igual ao número de vezes em que m < 25 dividir 252 sem deixar resto. Os divisores de 252
menores que 25, são: 1 e 5. Portanto, existem dois tijolos de Euler com o lado menor igual a 7.
Cálculo da diagonal MN do tijolo de Euler:
25 2  1
= 313
2.(1)
25 2  5 2
2º tijolo: p2 
= 65
2.(5)
1º tijolo: p1 
Cálculo das dimensões de cada tijolo de Euler:
1º tijolo: a = d – 1 = 25 – 1 = 24
b=7
c = p – k = 313 – 1 = 312
Verificação: p  a 2  b2  c 2  242  72  3122  313
2º tijolo: a = 25 – 1 = 24
b=7
c = 65 – 5 = 60
Verificação: p  242  72  602  65
Exemplo 3. O matemático Halcke encontrou apenas um tijolo de Euler com o menor lado
igual a 44. Quantos tijolos de Euler existem com o menor lado igual a 44?
Resolução.
Os divisores pares de 442, menores que
44
, são: 2, 4, 8 e 16. Portanto, m = 2, 4, 8, 16.
2
Cálculo das diagonais da base, das diagonais principais e das dimensões do tijolo de Euler
d1 
442  22
 485
2 x2
Os divisores de 4852, menores que 485, são: 1, 5, 25 e 97.
p1 
4852  1
 117613 , b = 44, a = d1 – m = 485 – 2 = 483 e c = p1 – k = 117613 – 1 = 117612
2
Verificação: p1  442  4832  1176122  117612
d1  442  4832  485
p2 
4852  52
 23525 , b = 44, a = 483 e c = 23525 – 5 = 23520
2 x5
Verificação: p2  4832  442  235202  23525
4852  252
p3 
 4717 , b = 44, a = 483 e c = 4717 – 25 = 4692
2 x25
Verificação: p3  4832  442  46922  4717
p4 
4852  97 2
 1261, b = 44, a = 483 e c = 1261 – 97 = 1164
2 x97
Verificação: p4  4832  442  11642  1261
442  42
d2 
 244
2 x4
Os divisores pares de 2442, menores que
244
, são: 2, 4, 8 e 16
2
2442  22
p5 
 14885 , b = 44, a = d2 – m = 244 – 4 = 240 e c = 14885 – 2 = 14883
2 x2
Verificação: p5  2402  442  148832  14885
p6 
2442  42
 7444 , b = 44, a = 240 e c = 7444 – 4 = 7440
2 x4
Verificação: p6  2402  442  74402  7444
p7 
2442  82
 3725 , b = 44, a = 240 e c = 3725 – 8 = 3717
2 x8
Verificação: p7  2402  442  3717 2  3725
2442  162
d2
244 2
=
é ímpar)
 1868,5 (p8 não é inteiro porque
2 x16
k
16
p8 
442  82
d3 
 125
2 x8
Os divisores de 1252, menores que 125, são: 1, 5 e 25
p9 
1252  1
 7813 , b = 44, a = d3 – m = 125 – 8 = 117, c = 7813 – 1 = 7812
2
Verificação: p9  117 2  442  78122  7813
p10 
1252  52
 1565 , b = 44, a = 117 e c = 1565 – 5 = 1560
2 x5
Verificação: p10  117 2  442  15602  1565
p11 
1252  252
 325 , a = 44, b = 117 e c = 325 – 25 = 300
2 x 25
Verificação: p11  1172  442  3002  325
d4 
442  162
b
442
 68,5 (d4 não é inteiro porque
é ímpar)

2 x16
m 16
Conclusão. Baseando-se nos resultados obtidos, chegou-se à seguinte conclusão: com a condição de a
diagonal MN do tijolo de Euler ser um inteiro, apenas a diagonal da base é um número inteiro. Sendo
assim, pode-se dizer que não existe tijolo de Euler perfeito. Como existem tijolos com as dimensões, a
diagonal principal e a diagonal da base número inteiro, então, pode-se dizer que existem tijolos de Euler
quase-perfeitos.
Desprezando-se a condição de a diagonal MN do tijolo ser um número inteiro, não é difícil, e sim
trabalhoso, achar as dimensões e as diagonais do tijolo determinadas pelo matemático Halcke.
44
.
2
Foi visto, anteriormente, que com os divisores 2, 4 e 8 foram encontradas as seguintes diagonais: d1
= 485, d2 = 244 e d3 = 125.
Como a menor dimensão do tijolo é 44, basta achar os divisores pares de 442 menores que
Subtraindo de 485, 244 e 125, respectivamente, os divisores 2, 4 e 8, obtém-se as seguintes
dimensões: 485 – 2 = 483, 244 – 4 = 240 e 125 – 8 = 117.
As dimensões do tijolo com as diagonais números inteiros são uma das três:
a
b
c
44
44
44
240
117
117
483
483
240
Como para cada diagonal da base do tijolo há duas dimensões, basta que combinemos três
dimensões duas a duas, e em seguida determinar a diagonal.
44e240 : d  442  2402  244
1


2
2
44e483 : d 2  44  483  485

2
2
240e483 : d3  240  483  539,34
44e117 : d  442  117 2  125
1


2
2
44e483 : d 2  44  483  485

2
2
117e483 : d3  117  483  496,97
44e117 : d  442  117 2  125
1


2
2
44e483 : d 2  44  240  244

2
2
117e240 : d3  117  240  267
As mesmas dimensões (44, 117 e 240) e as mesmas diagonais (125, 244 e 267) encontradas
pelo matemático Kalcke.
O autor é professor titular aposentado pela UFCG-PB