Noções de Função Derivada

Noções de Função Derivada
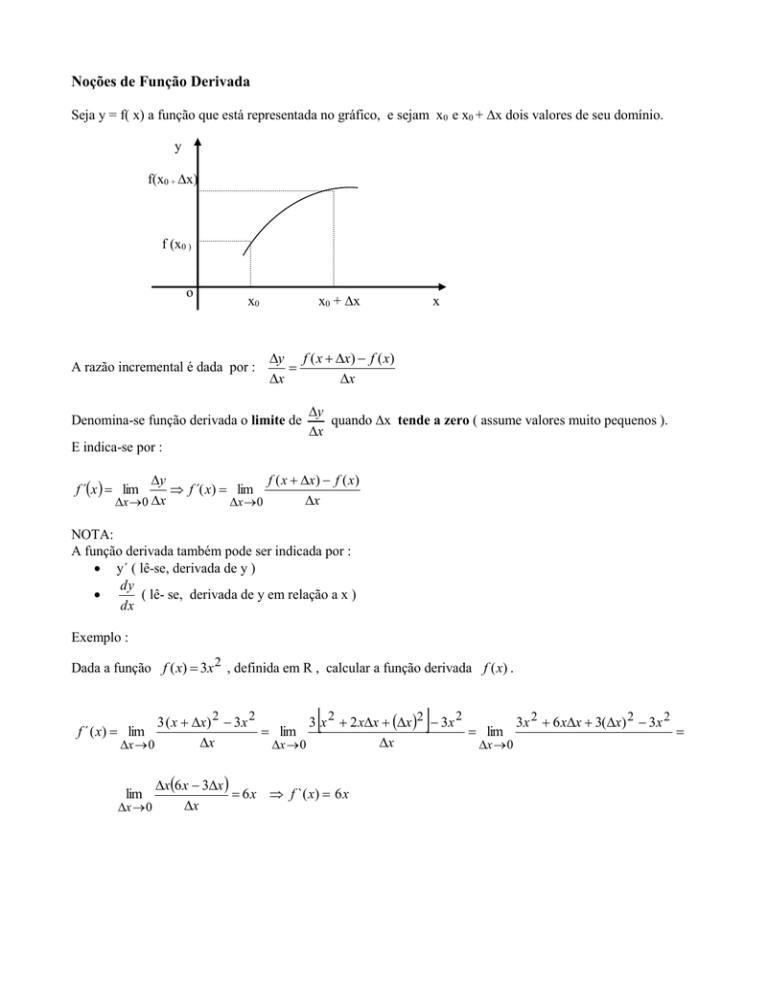
Seja y = f( x) a função que está representada no gráfico, e sejam x0 e x0 + x dois valores de seu domínio.
y
f(x0 + x)
f (x0 )
o
x0 + x
x0
A razão incremental é dada por :
x
y f ( x  x)  f ( x)

x
x
Denomina-se função derivada o limite de
y
quando x tende a zero ( assume valores muito pequenos ).
x
E indica-se por :
y
f ( x  x)  f ( x)
 f ´( x)  lim
x
x 0 x
x 0
f ´x   lim
NOTA:
A função derivada também pode ser indicada por :
 y´ ( lê-se, derivada de y )
dy

( lê- se, derivada de y em relação a x )
dx
Exemplo :
Dada a função f ( x)  3x 2 , definida em R , calcular a função derivada f (x) .


3 ( x  x) 2  3x 2
3 x 2  2 xx  x 2  3x 2
3x 2  6 xx  3(x) 2  3x 2
 lim
 lim

x
x
x  0
x  0
x  0
f ´ ( x)  lim
x6 x  3x 
 6 x  f `( x )  6 x
x
x  0
lim
Regras Fundamentais de Derivação:

Derivada da função constante : f ( x)  k

Derivada da função identidade : f ( x)  x é 1, ou seja : f ( x)  x  f ´( x)  1

Derivada da função potência : f ( x)  x n (n  *)  f ´( x)  nxn 1
; kR é nula, isto é :
f ( x)  k  f ´( x)  0
Exemplos:
1. f ( x)  x 3  f ´( x)  3x 3 1  f ´ ( x)  3x 2
2. f ( x)  4 x 2  f ´( x)  2  4 x 2 1  f ´ ( x)  8x
3. f ( x)  x  5  f ´( x)  5x  5 1  f ´ ( x)  5x  6  f `( x)  
5
x6

Derivada da função seno:

Derivada da função cosseno: f ( x)  cos x  f ´( x)   sen x

Derivada da função exponencial : f ( x)  a x (a  0 e a  1)  f `( x)  a x l na
f ( x)  sen x  f ´( x)  cos x
Exemplo:
f ( x)  5 x  f ´( x)  5 x l n5

Derivada da função logarítmica neperiana: f ( x)  l nx  f ´( x) 
1
x
CAPÍTULO 4 - Movimento em duas e em três Dimensões
4.1 – Considerações Gerais:
 Aqui serão estendidas as considerações apresentadas nos capítulo anterior para os casos bi e
tridimensionais. Vamos utilizar álgebra vetorial nos conceitos já vistos ( posição, velocidade,
deslocamento e aceleração )
4.2 – Posição e Deslocamento :
 Em geral, a localização de uma partícula é determinada pelo vetor posição r, que é um vetor que de
um ponto de referência ( geralmente a origem de um sistema de coordenadas ) até a partícula. Pela
notação de vetores, escrevemos r como :
r = xi + yj + zk , onde xi , yj e zk são as componentes vetoriais de r, e os coeficientes x, y e z são
as componentes escalares.
y
2j
5k
-3i
P

O
x
r
z
Ao longo do eixo x, P está 3 unidades da origem, no sentido –i . Ao longo do eixo y, está à duas unidades
da origem, no sentido +j . E, ao longo do eixo z, está a 5 unidades da origem, no sentido +k.
Ex.: Inicialmente, o vetor posição de uma partícula é r1 = -3i + 2j + 5k e logo depois é r2 = 9i + 2j + 8k .
Qual é o deslocamento de r1 para r2 ?
Solução :
r = r2 – r1 = ( 9i + 2j + 8k ) – ( -3i + 2j + 5k ) = 12i + 3k
Nota :
Este vetor deslocamento é paralelo ao plano xz, porque sua componente y é nula; um fato constatado
pelo resultado numérico.
4.3 – Velocidade e Velocidade Média:
 Uma partícula que sofre um deslocamento r, durante um intervalo de tempo t , tem velocidade
média:
v
r
t

xi  y j  z k
t

v
x
y
z
i
j
k
t
t
t
A velocidade instantânea v é o limite de v , quando t tende para zero. Lembramos que esse limite é a
derivada de r em relação á t ou seja, v 
v


d
dx dy
dz
xi  y j  z k  i 
j k
dt
dt
dt
dt
dr
; Substituindo r pela expressão r = xi + yj + zk , temos :
dt

v  vx i  v y j  vz k
os coeficientes são as componentes escalares de v: v x 
;
dx
dy
dz
; vy 
; vz 
dt
dt
dt
y
tangente à curva
P

r1
o
r
Trajetória de P
r2
x
A posição da partícula P, na sua trajetória, é mostrada no instante t1 e no instante t1 + t seguinte. O vetor
r é o deslocamento da partícula, no intervalo t. Também é mostrada a tangente à trajetória no instante t1.
NOTA :
No limite, quando t tende a zero, a velocidade média tende para v ( velocidade instantânea ) , e
também, a velocidade média tem a direção da tangente. Logo, v também tem a mesma direção, isto é,
sempre tangente à trajetória da partícula.
4.4 – Aceleração e Aceleração Média:
 Quando a velocidade de uma partícula varia de v1 para v2, no intervalo de tempo t, sua aceleração
média a , durante este intervalo de tempo é :
v v
v
a 2 1 
t
t
dv
dt
Quando a velocidade varia em módulo e/ou direção, significa que existe uma aceleração:
Aceleração instantânea a é o limite de a quando t tende a zero, ou seja, a 
a
d
(v x i  v y j  v z k ) ou
dt
a
dv y
dvx
dv
i
j z k
dt
dt
dt

a  ax i  a y j  az k
onde as três componentes escalares do vetor aceleração são:
ax 
dvx
dt
;
ay 
dv y
e
dt
az 
dvz
dt
y
P

ax
Trajetória de P
ay
a
x
o
Exemplo 1: Uma lebre atravessa correndo um estacionamento de veículos . A trajetória percorrida pela
lebre é dada pelas componentes do seu vetor posição com relação à origem das coordenadas, que são
função do tempo:
x = -0,31t2 + 7,2t + 28
e
y = 0,22t2 – 9,1t + 30
As unidades dos coeficientes numéricos nessas equações são tais que , se substituirmos t em segundos,
obteremos x e y em metros.

a) Calcule o vetor posição r da lebre (módulo e direção) em t=15 s :
x = ( - 31) ( 15 )2 + ( 7,2 )( 15 ) + 28 = 66 m
;
y = ( 0,22 )( 15 )2 – ( 9,1 )( 15 ) + 30 = -57 m
Módulo do vetor r : r  x 2  y 2  (66m) 2  (57 m)  87 m
Direção do vetor r : o ãngulo  que r faz com o semi-eixo positivo x é :
y
  57 m 
o
  tan 1  tan 1
  41
x
 66m 
Nota : Embora a tangente de  = 139o seja igual à de  = -41o, não consideraremos o ângulo de 139o, por
ser incompatível com os sinais das componentes de r.

b) Calcule o módulo e a direção do vetor velocidade da lebre em t = 15s.


dx d

 0,31t 2  7,2t  28  0,62t  7,2
dt dt
Em t = 15s, obtemos : v x   0,62 15   7,2  2,1m / s
Componente da velocidade na direção x : v x 


dy d

0,22t 2  9,1t  30  0,44t  9,1
dt dt
Em t = 15s, obtemos ; v y  0,44 15  9,1  2,5m / s
Componente da velocidade na direção y : v y 
Módulo do vetor v : v  v x 2  v y 2 
Direção do vetor v :   tan 1
 2,1m / s 2  (2,5m / s) 2
 3,3m / s
  2,5m / s 
 tan 1 
  tan 1 1,19  130 o
vx
  2,1m / s 
vy
Nota : Embora o ângulo de 50o tenha a mesma tangente, os sinais das componentes indicam que o ângulo
desejado está no terceiro quadrante, ou seja, 50o – 180o = -130o, O vetor velocidade é tangente à trajetória
da lebre e aponta na direção em que ela está correndo, em t = 15s.

c) Calcule também o módulo e a direção do vetor aceleração em t = 15s .
dvx d
  0,62t  7,2  0,62m / s 2
dt
dt
dv y
d
 0,44t  9,1  0,44 m / s 2
Componente da aceleração na direção y : a y 
dt
dt
Componente da aceleração na direção x : a x 
Observamos que a aceleração é invariável com o tempo, Podemos verificar que o vetor a tem módulo
e direção constantes em toda trajetória , (os cálculos são semelhantes ao item b).
Exemplo 2 : Uma partícula com velocidade v 0  2,0i  4,0 j (em m/s2 ) em t = 0 está sob uma aceleração
constante a , de módulo igual a 3,0 m/s2 , fazendo um ângulo  = 130° com o semi-eixo positivo x . Qual a
velocidade v da partícula em t = 2,0 s , na notação dos vetores unitários, assim como seu módulo e direção
(em relação ao semi-eixo positivo x) ?
Solução : Como a é constante, a equação v  v 0  at é aplicável ; entretanto , deverá ser usada
separadamente para calcular vx e vy (as componentes x e y do vetor velocidade v ), pois as componentes
variam de maneira independente uma da outra. Encontramos então
v x  v0 x  a x t
e
v y  v0 y  a y t
Onde v0x (= - 2,0m/s) e v0y (= 4,0 m/s) são as componentes x e y de v0 , e ax e ay são as componentes x e y
de a . Para determinar ax e ay , decompomos a com o auxílio da equação a x  a cos  e a y  a sen 
a x  a cos  = ( 3,0 m/s2) (cos 130°) = - 1,93 m/s2 ,
a y  a sen  = ( 3,0 m/s2) (sen 130°) = + 2,30 m/s2 .
Substituindo esses valores em vx e vy , temos
vx = - 2,0 m/s + (-1.93m/s2) (2,0s) = -5,9 m/s ,
vy = 4,0 m/s + (2,30m/s2) (2,0s) = 8,6 m/s ,
Então , em t = 2,0 s, temos
v = (-5.9m/s)i + (8,6 m/s)j
4.5 – Movimento de Projéteis:
É o movimento de uma partícula que executa um movimento bidimensional ( horizontal e vertical ) com
aceleração g de queda livre para baixo. N a análise desse movimento desprezaremos os efeitos da resistência do
ar.
O projétil( a partícula ) é lançado em x0 = 0 e y0 = 0 com velocidade inicial , v0 = v0x i + v0yj .

No gráfico abaixo são mostradas a velocidade inicial e as velocidades, com suas componentes escalares,
em vários pontos da trajetória.

A componente horizontal da velocidade permanece constante, ao tempo em que a componente vertical
da velocidade varia sob a ação da gravidade.

O alcance R é a distância horizontal do ponto de lançamento, até o ponto em que o projétil volta à
mesma altura do lançamento.
y
v
vy = 0
v0
v0y
0
v0x
0

vx
R
vy

x
v
O Movimento Horizontal :
Como não existe aceleração n a direção horizontal, a componente horizontal da velocidade permanece constante
durante o movimento.
O deslocamento horizontal x – x0 a partir de uma posição inicial x0 é dado pela equação:
x - x0 = ( v0cos )t
 Movimento Vertical :
O movimento vertical segue a análise do movimento de uma partícula em queda livre. As equações a serem
utilizadas são :
;
y  y0  v 0 sen 0 t 
1 2
gt
2
v y  v 0 sen 0  gt
v y 2  v 0 sen  0 2  2 g  y  y 0 
Onde

v 0 y  v 0 sen 0
Equação da Trajetória ( caminho percorrido pelo projeto ):


g
x2
y  tan  0 x  
 2v cos  2 
0 
 0

Alcance Horizontal :
v 2
R  0 sen 20
g
;
Note que R atinge seu valor máximo, quando sen 2  1  2  90 o , i.é ,   45 o
y  altura final
t  tempodecorrido
y 0  altura inicial
 0  ângulo de inclinação de lançamento
v 0  velocidade vertical inicial
g  aceleraçâoda gravidadelocal
v y  velocidade vertical final
R  alcance horizontal
Os Efeitos do Ar
y
II
I
60°
x
A trajetória das duas bolas
Trajetória I (Ar)
97 m
52 m
6,6 s
Alcance
Altura máxima
Tempo de percurso
Trajetória II (Vácuo)
175 m
75 m
7,9 s
O ângulo de lançamento é de 60° e a velocidade de lançamento é de 160 km/h.
(I) A trajetória do lançamento de uma bola, levando em conta a resistência do ar (calculada por computador).
(II) A trajetória que a bola teria no vácuo, calculada pelos métodos já conhecidos.
y
Exemplo :
v0
Um avião de salvamento está voando a uma
x
0
altitude constante de 1.200m à velocidade de
tra
je
430 km/h, numa trajetória diretamente sobre o
h
ponto em que uma pessoa está se debatendo na
lin
ha
de
tó
ria
mi
ra
água. Em que ângulo  de mira o piloto deve
lançar a cápsula de salvamento, para que esta
caia bem próximo à pessoa?
v
A velocidade inicial da cápsula é a mesma do avião. Isto é, a velocidade inicial v0 é horizontal, e vale 430 km/h.
Podemos calcular o tempo de vôo da cápsula,
y  y 0  ( v 0 sen  0 )  1 gt 2
2
origem)
t 
e
0
=
0,
Fazendo y – y0 = 1.200 m (o sinal menos significa que a pessoa está abaixo da
obtemos:
21.200 m   15,65 s .
9,8m / s 2
 1.200 m  0  1 (9,8m / s 2 ) t 2 .
2
Resolvendo
para
t,
achamos
Assim obtemos a distância horizontal percorrida pela cápsula (e pelo avião ) durante esse tempo:
x  x 0  ( v 0 cos  0 ) t = (430 km/h) (cos0° ) (15,665 s) ( 1h / 3600 s) = 1,869 km
= 1.869 m
Se x0 = 0, então x = 1.869 m . O ângulo de mira então é   tan 1 x  tan 1 1869 m  57
h
1200 m
Como o avião e a cápsula têm a mesma velocidade horizontal, o avião permanece verticalmente sempre sobre
a cápsula, enquanto ela estiver voando.
Exemplo : Num filme publicitário, um ator corre pelo telhado de um prédio e salta, na horizontal, para o
telhado de outro prédio mais abaixo, conforme mostrado na figura. Antes de tentar o salto, sabiamente quer
avaliar se isto é possível. Ele pode realizar o salto se sua velocidade máxima sobre o telhado for de 4,5 m/s ?
4,5 m/s
4,8 m
6,8 m
Ele levará um tempo para cair 4,8 m, o que pode ser determinado pela equação y  y 0  ( v 0 sen  0 )  1 gt 2 .
2
Fazendo y – y0 = - 4,8 m (observe o sinal) e 0 = 0, e utilizando a equação dada acima , obtemos
t 

2 ( y  y0 )

g

(2) (4,8m)
9,8m / s 2
 0,990 s
Agora perguntamos: “ Que distância ele alcançará horizontalmente nesse tempo? ”
x  x 0  ( v 0 cos  0 ) t = ( 4,5 m/s ) (cos 0°) (0,990 s) = 4,5 m
Para alcançar o outro prédio, o homem teria de se deslocar 6,2 m na horizontal). Logo, o conselho que damos ao
ator é : “Não salte.”
Exemplo :
y
63°
27°
x
R= 560 m
Nesta distância, o canhão de defesa do porto pode atingir o navio pirata estando em dois ângulos de elevação diferentes
A figura mostra um navio pirata ancorado a 560 m de um forte, que defende a entrada de um porto, em uma
ilha. O canhão de defesa está localizado ao nível do mar e tem uma velocidade de tiro de 82 m/s .
a)
Qual o ângulo de elevação do canhão para atingir o navio pirata ?
2
v
Resolvendo a equação R  0 sen 2 0 para 20 , obtemos
g
2 0  sen 1
(9,8 m / s 2 ) (560 m )
gR
 sen 1
 sen 1 0,816 .
2
2
v0
(82 m / s )
Há dois ângulos cujo seno é 0,816, ou seja 54,7° e 125,3°. Logo, achamos  0  1 (54,7)  27
2
e
 0  1 (125,3)  63
2
O comandante do forte pode ordenar qualquer uma dessas elevações para o canhão atingir o navio pirata (se não
houver influência do ar!).
b)
Qual o tempo de percurso do projétil, até alcançar o navio, para cada um dos dois ângulos de elevação
calculados anteriormente ?
Calculando t para 0 = 27°, temos
t
x  x0
560 m

 7,7 s
v 0 cos  0 (82 m / s ) (cos 27 )
Repetindo o cálculo para 0 = 63°, obtemos t = 15 s . O que é razoável pois o tempo de percurso para
maiores ângulos de elevação deve ser, também, maior.
c)
A que distância do forte deve ficar o navio pirata, para se manter fora do alcance do canhão ?
Vimos que o alcance máximo corresponde a um ângulo de elevação 0 de 45° na equação de alcance
horizontal, temos
v 2
(82 m / s ) 2
R  0 sen 2 0
sen (2 x 45)  690 m
g
9,8m / s 2
À medida que o navio pirata se afasta, os dois ângulos de elevação com que o navio pode ser atingido se
aproxima, tendendo para 0 = 45° quando o navio está a 690 m de distância. Além desse ponto, o navio está
a salvo.
4.6 – Movimento Circular Uniforme:

Uma partícula está em movimento circular uniforme se percorre um círculo ou arco circular com
velocidade constante.

O fato de v ser um vetor, faz com que a partícula esteja acelerada devido à mudança de direção deste .

A aceleração responsável pela mudança de direção da partícula é a aceleração centrípeta( a c 
v2
).
r
y
vp
P


vpy
P
q

vpx
r
r

vqx

vqy
vq

O
x
Uma partícula se desloca em movimento circular uniforme, com velocidade constante v, num círculo de raio r.
Suas velocidades nos pontos P e q , eqüidistantes do eixo y, são vp e vq, dadas por suas componentes horizontal
e vertical, naqueles pontos.
A aceleração instantânea da partícula, em qualquer ponto, tem módulo
v2
e aponta para o centro do círculo.
r
v

a
O
v

a
a

v
Os vetores velocidade e aceleração para uma partícula em movimento circular uniforme. Os módulos são
constantes, mas as direções variam continuamente.
Não há uma relação fixa entre a direção do vetor velocidade e a direção do vetor aceleração.
A figura abaixo mostra exemplos em que o ângulo entre esses dois vetores varia de 0o e 180o.

180° > 
90° > 


v

v
v
a
a
Projétil atirado
para cima

a
Lançamento de um
projétil


a
Projétil na posição
de altura máxima
a
Queda de um projétil
v
v
Projétil atirado
para baixo