Unidade: Os Números Reais. Inequações
Regência n.º 4
Lição n.º 69 e 70
3 de Fevereiro de 2009
Sumário:
Noção de inequação. Resolução de inequações do 1.º grau a uma incógnita.
9.º D
Comentário:
A planificação destinase a uma aula de 90
minutos.
Tópicos
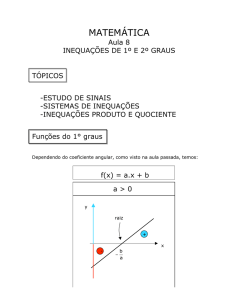
Resolução de inequações do 1.º grau a uma incógnita.
Conhecimentos Prévios
Resolver equações do 1.º grau
Conhecer os símbolos: “<”, “>”, “”, “”
Representação geométrica e representação por uma condição de um intervalo
Intervalos "abertos "e "fechados"
Intervalos limitados e ilimitados
Conhecimento e significado do símbolo infinito
Representar subconjuntos de números reais na recta real
Objectivos
Resolver inequações do 1.º grau a uma incógnita
Verificar se um número é solução de uma inequação
Representar o conjunto solução de uma inequação na recta real
Usar inequações como meio de representar situações problemáticas;
Formato de Ensino
Resolução de exercícios em pares
Discussão grupo-turma
Actividade Motivacional
1. Num clube de ginástica há duas modalidades para os seus praticantes:
Modalidade A: uma mensalidade de 40€ acrescida de 5€ por sessão
Modalidade B: uma mensalidade de 60€ acrescida de 2,5€ por sessão
Comentários:
A tarefa tem como
objectivo introduzir as
inequações. Será dado
tempo para os alunos
reflectirem sobre o
exercício.
Quantas sessões, por mês, são necessárias para que a modalidade B seja mais
vantajosa economicamente?
Exploração
1. Pedir aos alunos que defina as expressões que representam o pagamento da
modalidade A e modalidade B.
2. Analisar as propostas dos alunos de resolução da actividade motivacional.
Comentários:
Será dado aos alunos
algum tempo para
reflectirem sobre a
tarefa da actividade
motivacional e
respectiva resolução.
Os alunos apresentarão
as suas sugestões e a
partir delas, tentar
resolver a situação da
actividade motivacional.
Caso os alunos, nas suas
sugestões não fizerem
uma abordagem
relacionada com as
inequações, a
Professora irá sugerir
uma outra forma de
resolver a situação em
questão, introduzindo o
conceito de inequação.
3. Estabelecer a noção de inequação, os seus membros e termos.
Marta Mendes
1
Unidade: Os Números Reais. Inequações
Regência n.º 4
4. Resolver a inequação que traduz a situação da actividade motivacional.
Actividades práticas
1. Das seguintes expressões indica, justificando, as que são inequações:
2x 7 5
b) 3x 1,75 4 5,9 x
a)
x2 4 0
d) 7 x 5 3x 2
3
2 5
e)
5
c)
f)
x3 x 5,7 x
g)
x 7,6
9.º D
Depois de introduzido
conceito de inequação e
todos os seus conceitos
adjacentes, será pedido
aos alunos para
resolverem a inequação
da situação da
actividade motivacional.
Será questionado aos
alunos de como
poderão resolver a
inequação.
Para melhor
perceberem como se
pode obter o conjunto-solução de uma
inequação, será feita
uma analogia à
resolução de equações.
Todo este processo será
desenvolvido no quadro,
com a ajuda de alguns
alunos que serão
convidados a participar.
Comentário:
Os exercícios propostos
na ficha de apoio serão
resolvidos em pares ou
individualmente.
Posteriormente, será
pedido aos alunos para
corrigirem no quadro.
Com este exercício
pretende-se averiguar
se os alunos
compreenderam o
conceito de inequação
ou mesmo para
consolidar o que já
aprenderam.
14
6
3
5
2. Resolve as seguintes inequações e apresenta, geometricamente e em forma
de intervalo de números reais, o respectivo conjunto-solução:
a) 3x 1 4 5x
b) 5(3,7 x) 0,5 x
c)
x 2 2 x 1
4
3
6
d)
x 1
2( x 1,3)
7,98
3
5
3. Traduz para linguagem matemática o seguinte enunciado e, de seguida,
determina o seu conjunto solução: “A soma de um número com seis é menor
do que o triplo desse número.”
Tarefa adicional
1. O pai da Ana foi contratado para vender um modelo de computadores, cujo
preço unitário é de 600 euros. Por mês, ele recebe uma quantia fixa de 200
euros. Para além deste valor, recebe ainda, por cada computador que vender,
12% do seu preço. Qual é o número mínimo de computadores que ele terá de
Marta Mendes
Comentário:
Consoante o ritmo de
trabalho apresentado
pela turma, a
Professora poderá
propor a resolução de
mais exercícios,
2
Unidade: Os Números Reais. Inequações
Regência n.º 4
vender, num mês, para receber mais do que 1500 euros, nesse mês?
Apresenta todos os cálculos que efectuares.
2.
Numa capoeira há galinhas brancas e galinhas castanhas. As galinhas brancas
põem o dobro dos ovos das galinhas castanhas. Numa semana, seis galinhas
brancas e três galinhas castanhas puseram mais de trinta ovos. Quantos ovos
pôs cada galinha branca?
Síntese final
Regista, no teu caderno, o que aprendeste hoje. Que dificuldades sentes?
A partir dos teus apontamentos, vamos escrever o sumário desta aula…
9.º D
salvaguardando-se,
também, que o trabalho
que não for efectuado
na aula será proposto
para trabalho de casa
para entregar na aula
seguinte.
Comentários:
A síntese final consistirá
na consolidação do que
foi abordado/estudado
pelos alunos na aula.
Os alunos, com a ajuda
da Professora, irão
construir uma conclusão
da aula e a partir dessa
conclusão escrever o
sumário da aula.
Avaliação
A avaliação do aluno incidirá nos seguintes itens:
Participação dos alunos nas tarefas propostas (qualidade e pertinência das intervenções)
Contribuição dos alunos na apresentação e discussão dos processos e dos resultados das tarefas
Capacidade de comunicar utilizando linguagem matemática
Comportamento
Recursos
Quadro branco e caneta
Ficha de apoio
Manual adoptado
Marta Mendes
3