Aula 08 – Inequações de 1° e 2° graus

MATEMÁTICA
Aula 8
INEQUAÇÕES DE 1º E 2º GRAUS
TÓPICOS
-ESTUDO DE SINAIS
-SISTEMAS DE INEQUAÇÕES
-INEQUAÇÕES PRODUTO E QUOCIENTE
Funções do 1° graus
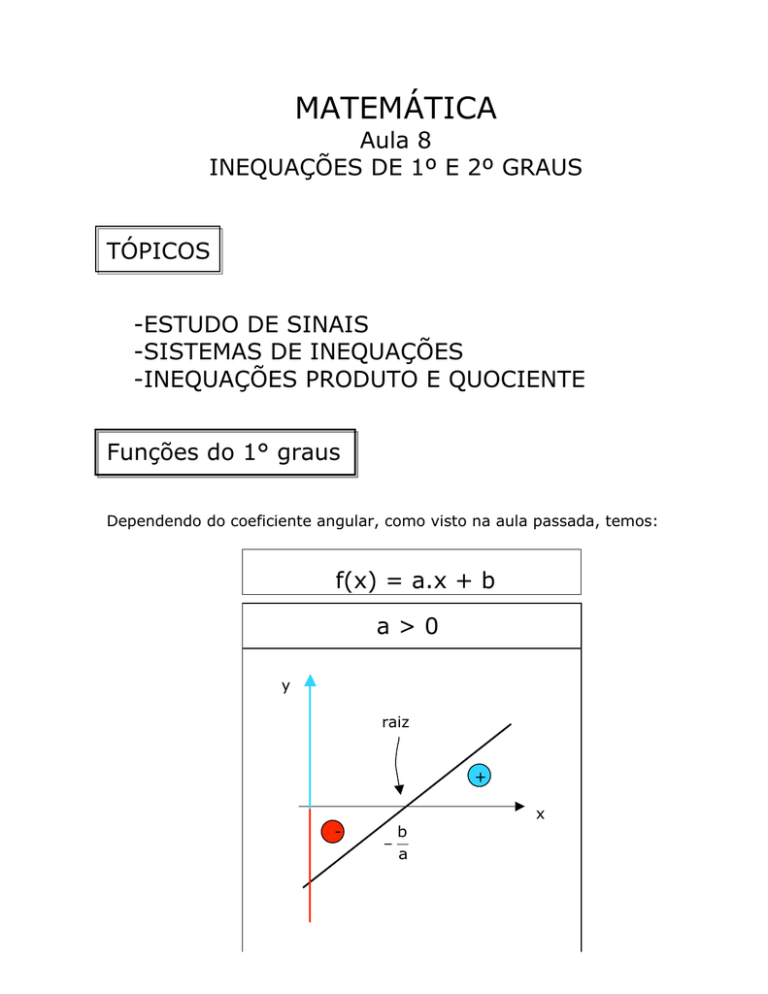
Dependendo do coeficiente angular, como visto na aula passada, temos:
f(x) = a.x + b
a>0
y
raiz
+
x
-
-
b
a
f(x) = a.x + b
a<0
y
raiz
+
x
-
-
b
a
Genericamente temos:
f(x) = a.x + b
f(x) tem sinal contrário de a
f(x) tem o sinal de a
x
-
b
a
Exemplo de Inequação de 1°grau
Para que valores de x a função f(x) = 4 - 2.x é positiva?
Resolvendo pelas propriedades de desigualdade temos:
f(x) é positiva fi f(x) > 0
fi 4 - 2.x > 0
fi -2.x > -4
fi 2.x < 4
fi x < 2
S = {x Π / x < 2}
fi
Resolvendo pelo estudo de sinais temos:
I)
Raiz:
f(x) = 0
f(x) = 4 - 2.x > 0
fi 4 - 2.x = 0
fi -2.x = -4
fi 2.x = 4
fi x = 2
II)
f(x) = 4 - 2.x >0
a = -2 < 0
+
2
x
_
III)
S = {x Π / x < 2}
Funções do 2° graus
Dependendo do coeficiente a, como visto na aula passada, temos:
a>0
a<0
+
D>0
+
+
-
-
x
-
-
D=0
+
-
+
x
-
D<0
+
+
x
-
Exemplo de Sistema de Inequações
Ïx 2 - 6x + 5 £ 0
Ì
Ó2x - 4 > 0
Resolver o sistema
2
1) x - 6x + 5 £ 0
2
D = b - 4.a.c
2
D = (-6) - 4.1.5
D = 36 - 20
D = 16 > 0
x=
2
6+4
2
concavidade para cima
fi
+
+
1
x
5
-
2
x - 6x + 5 £ 0
+
+
•
1
•5
-
fi
=
2
2
=1
fi raízes dist int as
x=
a=1>0
6-4
S1 = {x Œ ¬ / 1 £ x £ 5}
x
=
10
2
=5
2)
2x - 4 > 0
fi
2x > 4
fi > 2
fi
3)
{
S2 = {x Π / x > 2}
S1 = {x Œ ¬ / 1 £ x £ 5}
S2 = {x Π / x > 2}
1
•
•
2
1
5
S2
o
o
2
S = {x Œ ¬ / 2 < x £ 5}
S1
•
5
S1 I S2
Exemplo de Inequação Quociente
2
Resolver, em ¬ ,
x - 6x + 5
x -3
£0
1) f(x) = x2 - 6x + 5
+
+
1
x
5
-
2) g(x) = x – 3
fi
Raiz: x – 3 = 0
-
x=3
+
3
x
2
3)
x - 6x + 5
x -3
£0
1
3
5
x
f(x)
+
-
-
+
g(x)
-
-
+
+
-
+
-
+
f(x)
g(x)
•
1
o
3
•
5
S = {x Œ ¬ / x £ 1 ou 3 < x £ 5}
Procure refazer os exemplos da aula.
Depois, pegue funções de 1° e 2° graus que você conhece e misture
formando sistemas, inequações quociente e inequações produto. Envie um
desses para verificação.