JOGOS - Programa Institucional de Bolsas de Iniciação à Docência

UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
PROGRAMA INSTITUCIONAL DE BOLSAS
DE INICIAÇÃO A DOCÊNCIA
SUBPROJETO MATEMÁTICA
Oficina 2 de preparação para o SAEB na Escola Agrônomo Pedro Pereira (8ª Série)
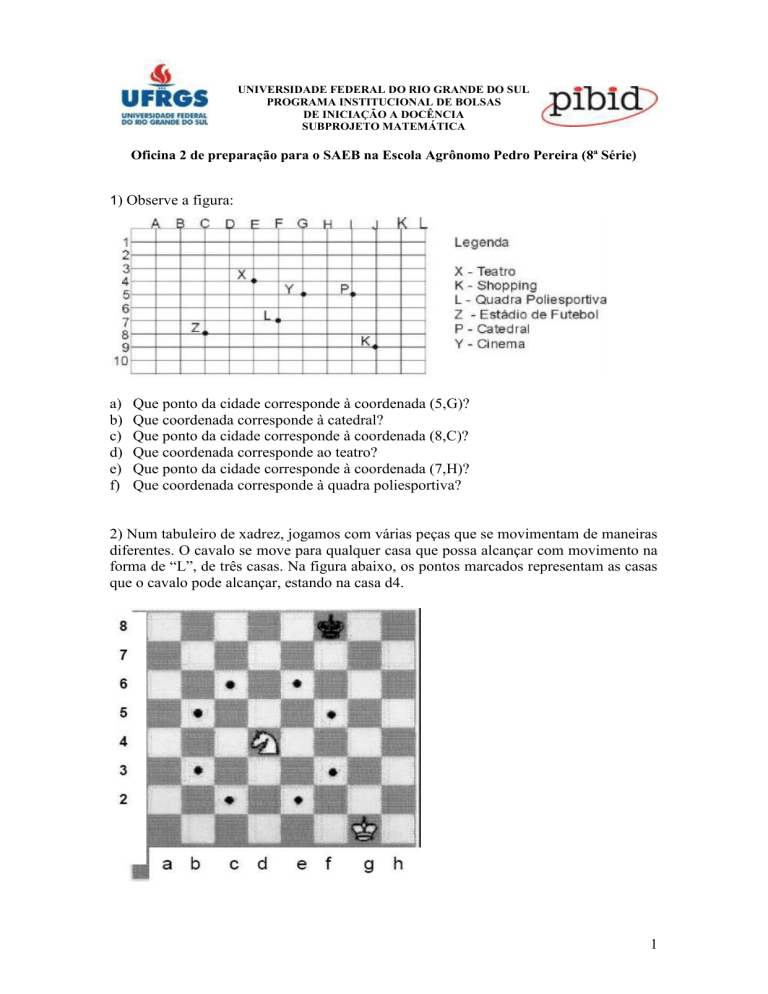
1) Observe a figura:
a)
b)
c)
d)
e)
f)
Que ponto da cidade corresponde à coordenada (5,G)?
Que coordenada corresponde à catedral?
Que ponto da cidade corresponde à coordenada (8,C)?
Que coordenada corresponde ao teatro?
Que ponto da cidade corresponde à coordenada (7,H)?
Que coordenada corresponde à quadra poliesportiva?
2) Num tabuleiro de xadrez, jogamos com várias peças que se movimentam de maneiras
diferentes. O cavalo se move para qualquer casa que possa alcançar com movimento na
forma de “L”, de três casas. Na figura abaixo, os pontos marcados representam as casas
que o cavalo pode alcançar, estando na casa d4.
1
Quais são as casas que o cavalo pode alcançar, partindo da casa f5 e fazendo uma única
jogada?
Tarefa para ser feita com as páginas amarelas da lista telefônica:
1) Localize no mapa a Rua Armando Barbedo. Anote abaixo o número da planta e
a coordenada onde localizou a rua.
2) Localize agora a Rua Cerro Azul. Anote abaixo o número da planta e a
coordenada onde localizou a rua.
3) Na planta 2, coordenada c4 temos o cruzamento da Rua Gomes de Freitas com a
Avenida Baltazar de Oliveira Garcia. Se saíssemos deste ponto, seguirmos pela
Rua Gomes de Freitas, entrarmos na 3ª rua à esquerda, depois na 2ª rua à direita,
depois na 4ª rua à esquerda, estaríamos em qual rua?
4) Localize no mapa a sua escola.
Tarefa para ser feita com o mapa de Porto Alegre:
1) Localize no mapa os seguintes pontos turísticos:
Aeroporto, Laçador, Mercado Público, Prefeitura, Casa de Cultura Mário Quintana,
Catedral Metropolitana, Usina do Gasômetro, Estádio Olímpico, Estádio Beira Rio.
2) Usando que 1 cm do mapa equivale a 100 m de distância real, faça uma rota
(independente das ruas) que o leve a todos os pontos turísticos acima
percorrendo a menor distância possível. Após, diga qual a distância percorrida
no mapa e a distância real percorrida.
2