onde n³ l+1, n é o número quântico principal e En corresponde aos

Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
39
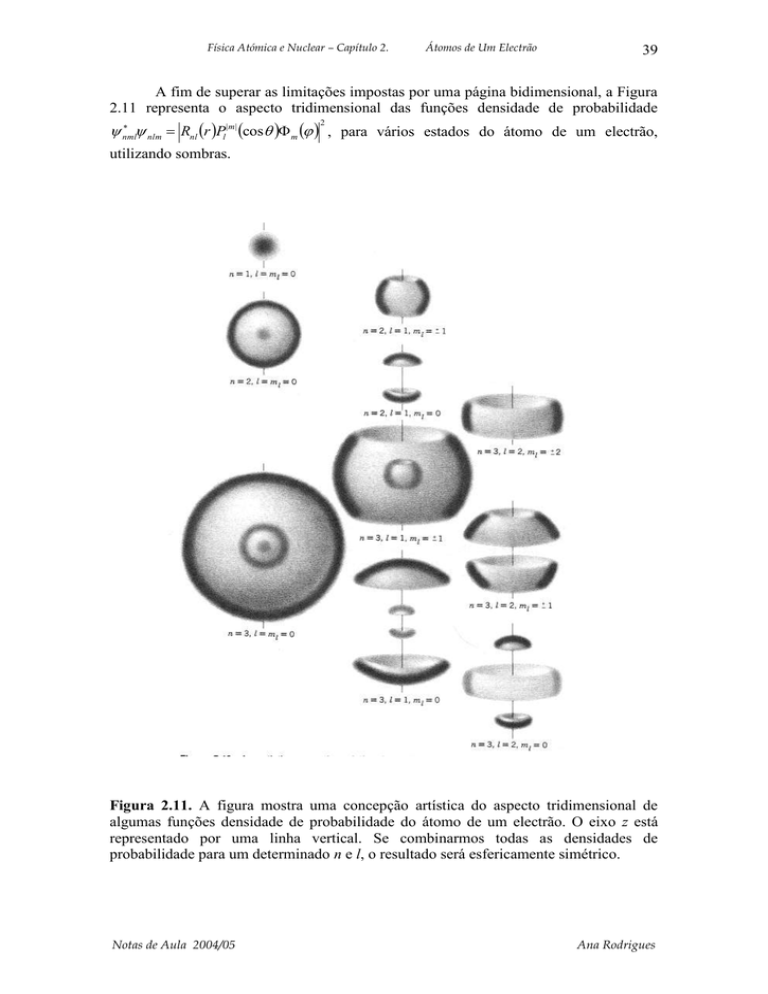
A fim de superar as limitações impostas por uma página bidimensional, a Figura
2.11 representa o aspecto tridimensional das funções densidade de probabilidade

 nml
 nlm  Rnl r Pl|m| cos  m   , para vários estados do átomo de um electrão,
2
utilizando sombras.
Figura 2.11. A figura mostra uma concepção artística do aspecto tridimensional de
algumas funções densidade de probabilidade do átomo de um electrão. O eixo z está
representado por uma linha vertical. Se combinarmos todas as densidades de
probabilidade para um determinado n e l, o resultado será esfericamente simétrico.
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
40
A energia En dos estados degenerados são idênticas, e não é possível
experimentalmente separá-los uns dos outros com técnicas que não perturbem a
densidade de probabilidade. Assim tudo o que pode ser medido é a densidade de
probabilidade média dos átomos, para todo o conjunto de estados que são degenerados
entre si. Quando se calcula a média dessa forma, geram-se funções esfericamente
simétricas.
Exemplo 2.3. Calcule a média das funções densidade de probabilidade para o conjunto de estados
degenerados correspondentes à energia E2.
Resolução:
Temos que:
n = 1, 2, 3….
l = 0,1, 2,…., n – 1.
M = -l, - l + 1,…...,0,…..... + l – 1, l.
Para n=2, l= 0,1e m=0,1,-1.

1 



 200 200   21
1 211   210 210   211 211
4

3
2
2
1  Z   Zr / a0 
Zr   Zr   1 2
1

  e
 2       sin   sin 2   cos 2  
=
128  a0 
a0   a0   2
2


3
2
2
1  Z   Zr / a0 
Zr   Zr  
 e
 2      
=
128  a0 
a0   a0  


Esta distribuição esfericamente simétrica será o resultado de uma sequência de medidas para localizar o
electrão, num átomo de um electrão de energia total E2.
______________________________________________________________________
Resumindo, podemos concluir que:
1º. Se o comportamento de um átomo é determinado por um potencial que tem simetria
esférica, como por exemplo o potencial Coulombiano, que depende somente da
distância do electrão ao núcleo, nenhuma das propriedades do átomo poderá seleccionar
qualquer direcção particular no espaço, porque todas as direcções são equivalentes.
2º. Se o átomo for colocado num campo externo, magnético (ou eléctrico), a simetria
esférica fica destruída e a direcção definida pelo campo externo torna-se única.
3º. Quando existe uma direcção única, escolhemos um dos eixos do nosso sistema de
coordenadas nessa direcção preferencial porque isso simplifica a descrição da situação
física. Podemos escolher outras direcções mas isso complica desnecessariamente a
descrição matemática do problema. Por exemplo, no electromagnetismo, quando
tratamos o problema de um fio cilíndrico, é conveniente tomar um dos eixos do sistema
de coordenadas ao longo do eixo do cilindro.
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
41
4º. Convencionalmente, chamamos o eixo preferencial de eixo z. A convenção provém
provavelmente do sistema de coordenadas cilíndricas, onde o eixo em torno do qual
varia a coordenada angular é chamado de eixo z. Poderíamos, entretanto, chamar o eixo
preferencial tanto de x como de y.
5º. Mesmo na ausência de uma direcção preferencial, o que acontece quando não há
campo externo aplicado sobre o átomo, precisamos escolher alguma direcção arbitrária
no espaço do nosso sistema de coordenadas, como por exemplo o eixo z. Neste caso este
eixo z não é fisicamente único, mas é matematicamente útil e a sua escolha não tem
nenhuma interferência sobre as medidas.
Embora a teoria da mecânica quântica para um átomo de um electrão e o modelo
de Bohr tenham muitos pontos em comum, existem algumas diferenças notáveis entre
eles. Por exemplo, para ambos os tratamentos o estado fundamental corresponde ao
número quântico n=1 e tem o mesmo valor de energia. Mas no modelo de Bohr, o
momento angular orbital para esse estado é L  n   , enquanto que na mecânica
quântica L  l l  1  0 , porque l=0 quando n=1. Existem evidências experimentais,
de que o resultado quântico é o correcto. É difícil visualizar o movimento de um
electrão no estado fundamental mecânico quântico e é também igualmente difícil fazer
uma analogia com uma descrição clássica, como a descrição de Bohr. Existe outras
situações em que isso acontece, como por exemplo, visualizar o movimento de um
electrão atravessando um aparelho de difracção de duas fendas.
2.7 Momento Angular Orbital. Modelo Vectorial.
O momento angular de uma partícula, em relação à origem de um dado sistema de

coordenadas é a grandeza vectorial L definida por:
  
Lrp
(2.80)


onde r é o vector posição da partícula, em relação à origem e p é o vector momento



  


linear da partícula. Considerando que r  xi  yj  k e p  px i  p y j  pz k , podemos
calcular as componentes do vector em coordenadas cartesianas (rectangulares):

i
x
px

j
y
py

k



z  Lx i  Ly j  Lz k
pz
(2.81)
onde:
   
   
   
e Lˆ z  x  y
Lˆx  y  z , Lˆ y  z  x
i x i z
i z i y
i y i x
(2.82)
Convém transformar estas expressões em coordenadas esféricas:
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
42


 
Lˆx  i sin 
 cot g cos 


 



 
Lˆ y  i  cos 
 cot g sin 


 

(2.83)

Lˆx  i


O quadrado do módulo do vector L , definido como:
L2  L2x  L2y  L2z
(2.84)
O operador associado em coordenadas esféricas é:
 1
2
1  
 
Lˆ2   2  2

 sin 

2
sin   
 
 sin  
(2.85)
Os valores esperados de L̂ e L̂ z são:
Lz  m
(2.86)
L2  l l  1 2
(2.87)
O facto de  nlm não descrever um estado com componentes x e y do momento
angular orbital definidas – porque essas grandezas não são quantizadas – é do ponto de
vista da mecânica clássica, misterioso. Segundo a lei de conservação do momento
angular em mecânica clássica, o vector momento angular orbital de um electrão que se
move sob a influência de um potencial V r  esfericamente simétrico de um átomo de
um electrão, num espaço livre, estará totalmente fixo, em direcção e módulo, e todas as
componentes do vector terão valores definidos. O facto desse resultado não ser válido
na mecânica quântica é uma consequência de um princípio de incerteza que impõe não
ser possível conhecer com precisão total, simultaneamente, duas componentes do
momento angular. Como a componente z do momento angular orbital tem o valor
preciso m , a relação de incerteza exige que os valores das componentes x e y sejam
indefinidos. Verifica-se que Lx  Ly  0 . Não podemos dizer que sabemos que Lx
= L y =0, porque ao fazermos esta afirmação violamos o princípio da incerteza. Assim, a
orientação do vector momento angular orbital de um electrão, que se move num
potencial esfericamente simétrico, pode ser imaginada como variando sempre de forma
a que suas componentes x e y flutuem em torno de um valor médio nulo, enquanto sua
componente z e seu módulo permanecem fixos. Esse resultado pode ser chamado de
lei de conservação do momento angular orbital da mecânica quântica.
Muitas das propriedades do momento angular orbital podem ser
convenientemente representadas por esse modelo vectorial.
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
43
Figura 2.12. Representação dos vectores momento angular para os estados possíveis
com l  2 . Em cada estado o vector precessiona ao acaso em torno do eixo z, mantendo
um módulo (comprimento) constante e uma componente z constante.
A Figura 2.12 apresenta o modelo vectorial do momento angular para l=2 e
descreve os vectores momento angular para cada um dos cinco estados correspondentes
aos cinco valores possíveis de m, para l=2. Se cada um dos estados Lx e L y flutuam em
torno de seu valor médio nulo, os vectores descrevendo os estados precessarão ao acaso
em superfícies cónicas em torno do eixo z, satisfazendo a lei da conservação do
momento angular da mecânica quântica.
O número quântico m determina a orientação espacial do vector momento
angular orbital do átomo de um electrão. Portanto num certo sentido ele determina a
orientação espacial do próprio átomo. Como o potencial Coulombiano esfericamente
simétrico implica que não existe nenhuma direcção privilegiada no espaço no qual está
situado o átomo, podemos entender porque a teoria prevê que a energia total não
depende de m, que determina sua orientação. E assim podemos entender por que as
funções próprias são degeneradas em relação ao número quântico m. A energia do
átomo simplesmente não depende de sua orientação no espaço vazio.
Notas de Aula 2004/05
Ana Rodrigues