2 - (CEF/CESGRANRIO) Após a data de seu vencimento, uma

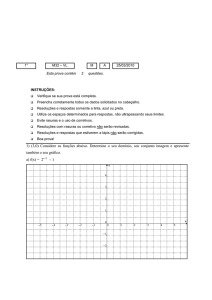
Prova da Caixa 2008
1) (CEF/CESGRANRIO) Em uma urna há 5 bolas
verdes, numeradas de 1 a 5, e 6 bolas brancas,
numeradas de 1 a 6. Dessa urna retiram-se,
sucessivamente e sem reposição, duas bolas.
Quantas são as extrações nas quais a primeira bola
sacada é verde e a segunda contém um número par?
(A) 15 (B) 20 (C) 23 (D) 25 (E) 27
Resolução:
A pergunta é: qual é o conjunto das possibilidades
de extrair primeiro uma bola verde e depois uma
bola par. Note que ao retirar a primeira bola verde,
temos duas opções: ela pode ser par ou ímpar.
Bolas verdes: V1, V2, V3, V4, V5
Bolas brancas: B1, B2, B3, B4, B5, B6
Assim, temos duas possibilidades:
1ª) Ou bola verde par e depois bola par:
Temos duas bolas verdes pares, ou seja, duas
possibilidades.
Bolas Verdes Par: V2, V4
Se retiramos 1 bola verde par, sobra uma bola verde
par e mais três bolas brancas e pares;
V2 ou V4, B2, B4, B6
portanto, sobram quatro possibilidades de bola par
para a segunda bola retirada, temos 2 ∙ 4 = 8
possibilidades para a primeira opção.
Log 10 2 = 0,3 e log 10 3 = 0,48
i = 8% am
Valor quitado: 190% do original.
Supor que o valor da dívida é R$100,00. Logo, o
valor quitado será de R$290,00.
M = C ∙ (1 + i) n + 2% ∙ C (multa)
290 = 100 ∙ (1 + i) n + 2% ∙ 100
290 = 100 ∙ (1 + i) n + 2
100 ∙ (1 + i) n = 290 – 2
100 ∙ (1 + i) n = 288
(1 + i) n = 2,88
Usando as propriedades dos logaritmos:
Log (1,08) n = log 2,88
n ∙ log (1,08) = log 2,88
n ∙ log
108
288
= log
100
100
n ∙ (log 108 – log 100) = log 288 – log 100
n ∙ (log 2² ∙ 3³ – log 10²) = log (2 5 ∙ 3²) – log 102
n ∙ (2 ∙ log 2 + 3 ∙ log 3 – 2) = 5 ∙ log 2 + 2 ∙ log3 –2
n[2 ∙ (0,30) + 3 ∙ (0,48) – 2] = 5 ∙ (0,30) + 2 ∙ (0,48)
–2
n ∙ (1,5 + 0,96 – 2) = 0,6 + 1,44 – 2
n = 1,5  0,96  2  0,46
0,6  1,44  2 0,04
n = 11,5 meses
2ª) Ou bola verde ímpar e depois bola par: para a
primeira bola verde e ímpar temos três opções.
Bolas Verdes ímpar: V1, V3, V5
3) (CEF/CESGRANRIO)
Sobram duas verdes e três brancas, num total de
cinco possibilidades de bolas pares.
Bolas pares: V2, V4, B2, B4, B6
Temos: 3 ∙ 5 = 15 possibilidades para a segunda
opção.
Em um caminho retilíneo há um canteiro formado
por 51 roseiras, todas enfileiradas ao longo do
caminho, como ilustrado. A distância entre
quaisquer duas roseiras consecutivas é 1,5 m. Nesse
caminho, há ainda uma torneira a 10,0 m da
primeira roseira.
Gabriel decide molhar todas as roseiras desse
caminho. Para isso, utiliza um regador que, quando
cheio, tem capacidade para molhar 3 roseiras.
Dessa forma, Gabriel enche o regador na torneira,
encaminha-se para a 1a roseira, molha-a, caminha
até a 2a roseira, molha-a e, a seguir, caminha até a
3a roseira, molhando-a também, esvaziando o
regador. Cada vez que o regador fica vazio, Gabriel
volta à torneira, enche o regador e repete a rotina
anterior para as três roseiras seguintes. No
momento em que acabar de regar a última das
roseiras, quantos metros Gabriel terá percorrido ao
todo desde que encheu o regador pela primeira vez?
(A) 1666,0 (B)
(B) 1581,0
(C) 1496,0
(D)
833,0 (E) 748,0
Ao todo teremos 8 + 15 = 23 possibilidades
2) (CEF/CESGRANRIO) Após a data de seu
vencimento, uma dívida é submetida a juros
compostos com taxa mensal de 8%, além de ser
acrescida de uma multa contratual correspondente a
2% da dívida original. Sabendo-se que log 10 2 =
0,30 e log 10 3 = 0,48 e utilizando-se para todo o
período o sistema de capitalização composta,
determine o tempo mínimo necessário, em meses,
para que o valor a ser quitado seja 190% maior do
que a dívida original.
(A) 24 (B) 23,5 (C) 13 (D) 11,5 (E) 10
Resolução:
Esta questão foi anulada por se muito complexa.
Dados:
1
Resolução: Este problema envolve PA que não
cai
para vocês neste concurso, mas está
resolvida abaixo:
De acordo com o enunciado, verificamos que para
sair da torneira, ir até a 3ª roseira e voltar, Gabriel
anda 26m. Depois para ir até a 6ª roseira e voltar,
35m, até a 9ª roseira e voltar 44m, e assim por
diante, formando uma progressão aritmética (P.A.),
(26, 35, 44, ...) de razão igual a 9 e com 17 termos,
já que calculamos de três em três roseiras e ao todo
são cinqüenta e uma (51: 3 = 17). Para calcular o
último (17º) termo desta P.A., basta utilizar a
fórmula geral ( a17 = a1 +16r) para encontrar: a17 =
170. Porém, note que devemos contar os metros até
o momento em que Gabriel acabar de regar a última
roseira, ou seja, para o último termo não contamos a
volta, que é de 85m (metade de 170).
Para chegar ao resultado, portanto, devemos somar
todos os termos da P.A. e depois subtrair 85. A
soma da
P.A. é dada por:
a  a  17 26  170 17
S17  1 17

 1.666
2
2
Vamos subtrair agora deste total do valor em que
ele não volta:
1.666 – 85 = 1.581 metros.
4) (CEF/CESGRANRIO) Um investimento consiste
na realização de 12 depósitos mensais de R$
100,00, sendo o primeiro deles feito um mês após o
início da transação. O montante será resgatado um
mês depois do último depósito. Se a taxa de
remuneração do investimento é de 2% ao mês, no
regime de juros compostos, o valor do resgate, em
reais, será:
(A) 1200,00
(B) 1224,00
(C) 1241,21
(D) 1368,03 (E) 2128,81
Resolução:
Questão sobre Rendas Certas:
(Imediata / Postecipada)
R = 100; n = 12; i = 2% am
Temos que o montante é: M= R ·
1  i 
12
M= 100 .
M  100 
Capitalização
1  i n  1
i
1
i
1,0212  1  100  1,268242  1.341,21
0,02
0,02
Como o montante será resgatado um mês após o
último depósito, temos que o valor de resgate:
M f  M  (1  i ) n  1341,21  (1  0,02)1
M f  1.368,03
5) (CEF/CESGRANRIO) A taxa efetiva anual de
510%, no sistema de juros compostos, equivale a
uma taxa nominal de i % ao semestre, capitalizada
bimestralmente. O número de divisores inteiros
positivos de i é:
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
Resolução:
Equivalência de Taxas
Taxa Efetiva (anual) = 50%
Taxa Nominal semestral = i% cap. Bimestralmente
(1 + ia) = (1 + ib)6
(1 + 0,5) = (1 + ib)6
1,5 = (1 + ib)6
Utilizando a tabela, teremos: i = 7%
Como o semestre tem 3 bimestres (taxa
proporcional), temos: 7% ∙ 3 = 21% ao semestre.
O número 21 possui os seguintes divisores:
D(21) = {1, 3, 7, 21}
n(21) = 4
6) (CEF/CESGRANRIO) A tabela abaixo apresenta
o fluxo de caixa de um certo projeto.
Período (anos)
Valor (Milhares de reais)
0
410
1
P
2
P
Para que a taxa interna de retorno anual seja 5%, o
valor de P, em milhares de reais, deve ser:
(A) 216,5
(B) 217,5
(C) 218,5
(D) 219,5
(E) 220,5
Resolução:
Questão sobre Equivalência de Capitais / Taxa
Interna de Retorno
Taxa interna de retorno (T.I.R.) = 5% aa
-- 410 (data zero) --- P (um ano) --- P (dois anos) -(Data focal no final)
410 é equivalente a P1 + P2 [com M = C . (1 + i) n ]
410(1 + 5%) 2 = P1(1 + 5%) 1 + P2(1 + 5%) 0
410 · 1,1025 = P · 1,05 + P
P = 452,025  220,50
2,05
7) (CEF/CESGRANRIO) Um empréstimo de R$
300,00 será pago em 6 prestações mensais, sendo a
primeira delas paga 30 dias após o empréstimo,
com juros de 4% ao mês sobre o saldo devedor,
pelo Sistema de Amortização Constante (SAC). O
valor, em reais, da quarta prestação será:
(A) 50,00
(B) 52,00
(C) 54,00
(D) 56,00
(E) 58,00
Resolução:
Questão sobre Sistema de Amortização Constante
(SAC)
n=6
i = 4%am
2
3ª – sair de 1 a 5 no primeiro e segundo
Amortização:
Empréstimo
300
A=

 50
prestações
6
J 1  A.(n  t  1)  i  50  (6  1  1)  0,04
lançamentos e 6 no terceiro: P =
5 5 1
25
  
6 6 6 216
J 2  50.(6  2  1)  0,04  10,00
Somando essas três probabilidades, chegamos à
conclusão de que a probabilidade de que N seja
menor do que 4 é de:
J 3  50.(6  3  1)  0,04  8,00
P=
J 1  12,00
J 4  50.(6  4  1)  0,04  6,00
P1  A  J 1  50,00  12,00  62,00
P2  A  J 2  50,00  10,00  60,00
P3  A  J 3  50,00  8,00  58,00
P4  A  J 4  50,00  6,00  56,00
Para calcular a 4ª prestação poderia ter resolvido
somente a Amortização, o J4 e o P4.
Sd1  Sd 0  A  300,00  50,00  250,00
Sd 2  Sd1  A  250,00  50,00  200,00
Sd 4  Sd 3  A  150,00  50,00  100,00
n Juros
Amortização Prestação Saldo
devedor
0
300,00
1 12,00 50,00
62,00
250,00
2 10,00 50,00
60,00
200,00
3 8,00 50,00
58,00
150,00
4 6,00 50,00
56,00
100,00
8) (CEF/CESGRANRIO) Joga-se N vezes um dado
comum, de seis faces, não viciado, até que se
obtenha 6 pela primeira vez. A probabilidade de
que N seja menor do que 4 é
150
216
25
(E)
216
(B)
91
216
(C)
75
216
(D)
55
216
Resolução:
Queremos N menor do que 4, ou seja, podemos
obter 6 na primeira vez, na segunda ou na terceira
vez em que lançarmos o dado. Assim, temos 3
possibilidades:
1ª – sair 6 no primeiro lançamento: P =
1
6
2ª – sair de 1 a 5 no primeiro lançamento e 6 no
segundo: P =
5 1 5
 
6 6 36
9) (CEF/CESGRANRIO) Júlio fez uma compra de
R$ 600,00, sujeita à taxa de juros de 2% ao mês
sobre o saldo devedor. No ato da compra, fez o
pagamento de um sinal no valor de R$ 150,00. Fez
ainda pagamentos de R$ 159,00 e R$ 206,00,
respectivamente, 30 e 60 dias depois de contraída a
dívida. Se quiser quitar a dívida
90 dias depois da compra, quanto deverá pagar, em
reais?
(A) 110,00
(B) 108,00
(C) 106,00
(D)
104,00 (E) 102,00
Resolução:
Questão sobre Equivalência de Capitais Compostos
Dívida: R$ 600 que será paga após 90 dias; i = 2%
ao mês.
Prestações diferentes em períodos diferentes.
-- 150 (já) -- 159 (1 mês) – 206 (2 meses) – Saldo
(3 meses)
Sd 3  Sd 2  A  200,00  50,00  150,00
(A)
1 5 25
91
+
+
=
6 36 216 216
1º. Calculando o valor dos pagamentos
150 ∙ (1 + 2%) 3 + 159 ∙ (1 + 2%) 2 + 206 ∙ (1 +
2%) 1 = X ∙ (1 + 2%) 0
150 ∙ (1,061) + 159 ∙ (1,0404) + 206 ∙ (1,02) =
X (saldo)
159,15 + 165,42 + 210,12 = X
X = 534,70
2º. Valor da dívida com 90 dias (3 meses)
N = A ∙ (1 + i)n
N = 600 ∙ (1 + 2%) 3
N = 600 ∙ 1,061
N = 636,70
3º. 636,70 (valor da dívida em 3 meses) – 534,70
(valor das parcelas da dívida)
Teremos o saldo de 636,70 – 534,70 = R$ 102,00.
10) (CEF/CESGRANRIO) Escrevendo-se todos os
números inteiros de 1 a 1111, quantas vezes o
algarismo 1 é escrito?
(A) 481 (B) 448 (C) 420 (D) 300 (E) 289
Resolução:
Vamos contar por blocos e desenvolver padrões:
- de 1 a 99 aparece 20 vezes o número 1.
3
- de 100 a 199 aparece 120 vezes o número 1
(análogo à primeira situação, porém o 1 aparece em
todos os números, na casa das centenas, por isso
100 +20).
- de 200 a 999 aparece 160 vezes o número 1 (200 a
299 – 20 vezes, 300 a 399 – 20 vezes, e assim por
diante).
- de 1000 a 1099 aparece 120 vezes o número 1.
(análogo à primeira situação, porém o 1 aparece em
todos os números, na casa das unidades de milhar,
por isso 100 +20)
- de 1100 a 1111 aparece 28 vezes o número 1.
(1100 a 1109 – 21 vezes, 1110 – 3 vezes e 1111 – 4
vezes).
Total = 448 vezes.
4