MATRIZES - escolareynaldomassi

Matriz (matemática)
Origem: Wikipédia, a enciclopédia livre.
Ir para: navegação, pesquisa
Na matemática, uma matriz é uma tabela de m x n símbolos sobre um corpo F, representada sob a
forma de um quadro com m linhas e n colunas e utilizado, entre outras coisas, para a resolução de
sistemas de equações lineares e transformações lineares.
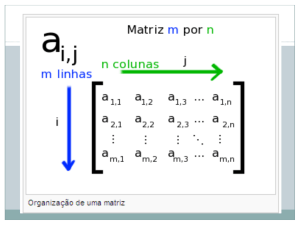
Organização de uma matriz

[editar] Notações e definições
As linhas horizontais da matriz são chamadas de linhas e as linhas verticais são chamadas de
colunas. Uma matriz com m(i) linhas e n(j) colunas é chamada de uma matriz m por n (escreve-se
m×n) e m e n são chamadas de suas dimensões, tipo ou ordem.
Um elemento de uma matriz A que está na i-ésima linha e na j-ésima coluna é chamado de elemento
i,j ou (i,j)-ésimo elemento de A. Ele é escrito como Ai,j ou A[i,j].
Uma matriz onde uma de suas dimensões é igual a 1 é geralmente chamada de vetor. Uma matriz 1
× n (uma linha e n colunas) é chamada de vetor linha ou matriz linha, e uma matriz m × 1(uma
coluna e m linhas) é chamada de vetor coluna ou matriz coluna.
Nas linguagens de programação, os elementos da matriz podem estar indexados a partir de 1
(Fortran, MATLAB, R (linguagem de programação), etc) ou a partir de 0 (C (linguagem de
programação) e seus dialetos). Por exemplo, o elemento A(1,1) em Fortran corresponde ao elemento
a[0][0] em C.
[editar] Exemplos
A matriz a seguir é uma matriz de ordem 2×3 com elementos naturais
Nesse exemplo, o elemento a1 2 é 2, o número na primeira linha e segunda coluna do quadro.
As entradas (símbolos) de uma matriz também podem ser definidas de acordo com seus índices i e
j. Por exemplo, aij = ixj, para i de 1 a 15 e j de 1 a 25, define a matriz 15x25 .
[editar] Algumas definições
A transposta de uma matriz Am × n é a matriz Atn × m em que , ou seja, todos os elementos da
primeira linha, tornar-se-ão elementos da primeira coluna, todos os elementos da segunda linha,
tornar-se-ão elementos da segunda coluna, todos os elementos da n linha, tornar-se-ão elementos da
m coluna. Exemplo:
Uma matriz é dita quadrada se tem o mesmo número de linhas e colunas, ou seja, quando podemos
dizer que, m tem a mesma quantidade de elementos que n. Numa matriz quadrada A de ordem n × n,
chama-se de diagonal principal os elementos aij onde i = j, para i de 1 a n.
A matriz identidade In é a matriz quadrada n × n que tem todos os membros da diagonal principal
iguais a 1 e 0 nas outras posições. Exemplo: .
A única matriz identidade que não contém zero é a matriz identidade de ordem 1:
Uma matriz A é simétrica se A = At. Isso só ocorre com matrizes quadradas.
[editar] Operações envolvendo matrizes
Este artigo ou secção não cita nenhuma fonte ou referência (desde junho de 2009)
Ajude a melhorar este artigo providenciando fontes fiáveis e independentes,
inserindo-as no corpo do texto ou em notas de rodapé. Encontre fontes: Google –
news, books, scholar, Scirus
Não se define adição ou subtração de um número com uma matriz, e nem divisões envolvendo
matrizes.
[editar] Multiplicação por um escalar
A multiplicação é uma das operações mais simples que podem ser feitas com matrizes. Para
multiplicar um número k qualquer por uma matriz m×n A, basta multiplicar cada entrada aij de A
por k. Assim, a matriz resultante B será também m×n e bij = k.aij. Com isso, pode-se pensar também
na noção de dividir uma matriz por um número: basta multiplicá-la pelo inverso desse número. Mas
essa noção pode ser perigosa: enquanto a multiplicação entre um número e uma matriz pode ser dita
"comutativa", o mesmo não vale para a divisão, pois não se pode dividir um número por uma
matriz.
Por exemplo:
[editar] Adição e subtração entre matrizes
Ver artigo principal: Adição de matrizes
Dado as matrizes A e B do tipo m por n, sua soma A + B é a matriz m por n computada adicionando
os elementos correspondentes: (A + B)[i,j] = A[i, j] + B[i,j].
Por exemplo:
Para melhorar a forma de calcular, você pode reescrever a segunda matriz, revertendo seus
elementos, onde o elemento (-1) passará para (1) e o elemento (2) passará para (-2) e assim
sucessivamente. Após feito isso, além de fazer A-B, você usará A+B.
Lembre-se: Você só pode fazer isso com Matriz negativa, onde recebe o sinal negativo, por
exemplo: em -A+B, o A que poderá ser reescrito.
[editar] Multiplicação de matrizes
Ver artigo principal: Produto de matrizes
Multiplicação de duas matrizes é bem definida apenas se o número de colunas da matriz da
esquerda é o mesmo número de linhas da matriz da direita. Se A é uma matriz m por n e B é uma
matriz n por p, então seu produto AB é a matriz m por p (m linhas e p colunas) dada por: Amxn.
Bnxp = ABmxp
para cada par i e j.
Por exemplo: que é praticamente igual à raiz quadrada)
A multiplicação de matrizes tem as seguintes propriedades:
z A e B m×n e matriz C k×m ("distribuição à esquerda").
É importante notar que a comutatividade não é geralmente garantida; isto é, dados as matrizes A e B
com seu produto definido, então geralmente AB ≠ BA.
Algoritmo para a multiplicação de uma matriz A por uma matriz B, sendo o resultado gravado
numa matriz C:
void multiply_matrix(int **A, int **B, int *C){
register unsigned i;
for (i=0; i<linhas(A); i++){
for (j=0; j<colunas(B); j++){
&C[i][j]=0;
for (x=0; x<colunas(A); x++){
&C[i][j]+=A[i][x]*B[x][j];
}
}
}
}
[editar] Propriedades
[editar] Determinante
Ver artigo principal: Determinante
O determinante é uma propriedade matricial útil na resolução de sistema de equações lineares (que
sempre podem ser representados através de matrizes), além de outras aplicações matemáticas.
[editar] Característica
A característica de uma matriz é um inteiro não negativo, que representa o número máximo de
linhas (ou colunas) da matriz que são linearmente independentes[1]. De acordo com o teorema de
Kronecker, temos que a característica de uma matriz B é C se e somente se:


Existe pelo menos uma submatriz c*c cujo determinante é diferente de zero.
Toda submatriz quadrada de ordem superior a c tem determinante zero.
Um menor de uma matriz é o determinante de uma de suas submatrizes. Logo, B tem a
característica C quando pelo menos uma de suas submatrizes tem um determinante C não nulo (seu
menor) e todo menor de ordem superior é igual a zero.
Se c for não nulo, então c é o maior inteiro não-negativo tal que B possui pelo menos uma
submatriz c * c com determinante diferente de zero. De acordo com a definição .
[editar]