matrizes - nordesttino

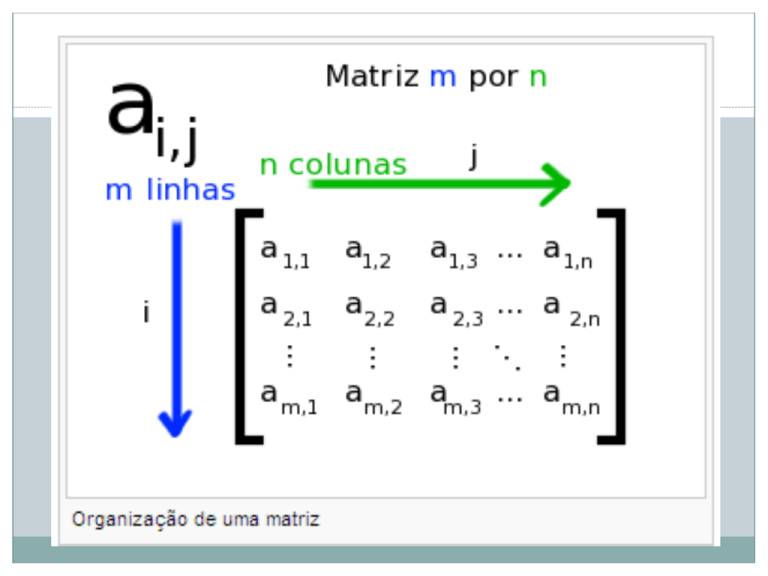
 As
linhas horizontais da matriz são
chamadas de linhas e as linhas verticais são
chamadas de colunas.
 Uma matriz com m linhas e n colunas é
chamada de uma matriz m por n (escreve-se
m×n) e m e n são chamadas de suas
dimensões, tipo ou ordem.
 Um elemento de uma matriz A que está na i-
ésima linha e na j-ésima coluna é chamado
de elemento i,j ou (i,j)-ésimo elemento de A.
 Ele é escrito como Ai,j ou A[i,j].
 Uma matriz onde uma de suas dimensões é
igual a 1 é geralmente chamada de vetor.
 Uma matriz 1 × n (uma linha e n colunas) é
chamada de vetor linha ou matriz linha,
e uma matriz m × 1(uma coluna e m linhas) é
chamada de vetor coluna ou matriz
coluna.
A matriz a seguir é uma matriz de
ordem 2×3 com elementos naturais
Matriz Geral
 A transposta de uma matriz Am × n é a
matriz Atn × m em que , ou seja, todos os
elementos da primeira linha, tornar-se-ão
elementos da primeira coluna, todos os
elementos da segunda linha, tornar-se-ão
elementos da segunda coluna, todos os
elementos da n linha, tornar-se-ão elementos
da m coluna.
RESUMINDO: Tocar linha por coluna.
Matriz
Transposta
 Uma matriz é dita quadrada se tem o
mesmo número de linhas e colunas, ou
seja, quando podemos dizer que, m tem a
mesma quantidade de elementos que n.
 Numa matriz quadrada A de ordem n ×
n, chama-se de diagonal principal os
elementos aij onde i = j, para i de 1 a n.
Operações envolvendo Matrizes
Multiplicação por um escalar
 A multiplicação é uma das operações mais simples que
podem ser feitas com matrizes.
 Para multiplicar um número k qualquer por uma matriz
n×m A, basta multiplicar cada entrada aij de A por k.
 Assim, a matriz resultante B será também n×m e bij = k.aij.
 Com isso, pode-se pensar também na noção de dividir uma
matriz por um número: basta multiplicá-la pelo inverso
desse número.
 Mas essa noção pode ser perigosa: enquanto a
multiplicação entre um número e uma matriz pode ser dita
"comutativa", o mesmo não vale para a divisão, pois não se
pode dividir um número por uma matriz.
Adição e Subtração entre Matrizes
 Dado as matrizes A e B do tipo m por n, sua soma A
+ B é a matriz m por n computada adicionando os
elementos correspondentes: (A + B)[i,j] = A[i, j] +
B[i,j].
Multiplicação de Matrizes
 Multiplicação de duas matrizes é bem definida
apenas se o número de colunas da matriz da
esquerda é o mesmo número de linhas da matriz da
direita.
 Se A é uma matriz m por n e B é uma matriz n por p,
então seu produto AB é a matriz m por p (m linhas
e p colunas) dada por:
Matrizes booleanas
 São matrizes que têm apenas elementos iguais a 0 ou
1.
 Podemos definir uma operação booleana de
multiplicação A×B para matrizes booleanas usando
multiplicação e soma booleanas, ao invés de
multiplicação e adição usuais.
operações booleanas de multiplicação e adição
 A multiplicação
booleana de
matrizes A X B é
definida por:
EXERCÍCIOS
 Multiplicação de matrizes
 O número de transistores e o número de alto-falantes
usados para montar três modelos de aparelhos de TV
foram especificados em uma tabela.