01 - (UNESP/2007) Em uma partida de futebol, a bola é chutada a

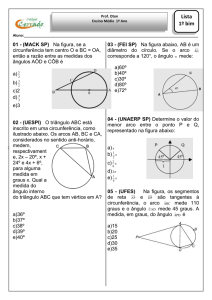
01 - (UNESP/2007)
Em uma partida de futebol, a bola é chutada a partir do
solo descrevendo uma trajetória parabólica cuja altura
máxima e o alcance atingido são, respectivamente, h e
s. Desprezando o efeito do atrito do ar, a rotação da
bola e sabendo que o ângulo de lançamento foi de 45º
em relação ao solo horizontal, calcule a razão s/h.
Dado: sen 450  cos 450  2 / 2
02 - (UNESP/2006)
Um garoto, voltando da escola, encontrou seus amigos
jogando uma partida de futebol no campinho ao lado de
sua casa e resolveu participar da brincadeira. Para não
perder tempo, atirou sua mochila por cima do muro,
para o quintal de sua casa: postou-se a uma distância
de 3,6 m do muro e, pegando a mochila pelas alças,
lançou-a a partir de uma altura de 0,4 m. Para que a
mochila passasse para o outro lado com segurança, foi
necessário que o ponto mais alto da trajetória estivesse
a 2,2 m do solo. Considere que a mochila tivesse
tamanho desprezível comparado à altura do muro e que
durante a trajetória não houve movimento de rotação ou
perda de energia. Tomando g = 10 m/s 2, calcule
a) o tempo decorrido, desde o lançamento, para a
mochila atingir a altura máxima.
b) o ângulo de lançamento.
03 - (UNESP/2006)
Dois blocos, A e B, com A colocado sobre B, estão em
movimento sob ação de uma força horizontal de 4,5 N
aplicada sobre A, como ilustrado na figura.
Considere que não há atrito entre o bloco B e o solo e
que as massas são respectivamente m A = 1,8 kg e mB =
1,2 kg. Tomando g = 10 m/s2, calcule
a) a aceleração dos blocos, se eles se locomovem
juntos.
b) o valor mínimo do coeficiente de atrito estático para
que o bloco A não deslize sobre B.
04 - (UNESP/2006)
Para determinar a velocidade de um projétil, um perito,
devidamente autorizado, toma um pequeno bloco de
madeira, com massa de 480 g e o coloca em repouso
na borda de um balcão horizontal de altura h = 1,25 m.
A seguir, dispara o projétil, de massa 20 g,
paralelamente ao balcão. O projétil penetra no bloco,
lançando-o ao solo, a uma distância d = 5,0 m da borda
do balcão, como ilustrado na figura.
Considerando g = 10 m/s2 e desprezando os efeitos de
atrito com o ar e o movimento de rotação do projétil e do
bloco, calcule
a) a velocidade com que o bloco deixa o balcão.
b) a velocidade do projétil obtida pelo perito.
05 - (UNESP/2008)
Pesquisadores têm observado que a capacidade de
fertilização dos espermatozóides é reduzida quando
estas células reprodutoras são submetidas a situações
de intenso campo gravitacional, que podem ser
simuladas usando centrífugas. Em geral, uma centrífuga
faz girar diversos tubos de ensaio ao mesmo tempo; a
figura representa uma centrífuga em alta rotação, vista
de cima, com quatro tubos de ensaio praticamente no
plano horizontal.
As amostras são acomodadas no fundo de cada um dos
tubos de ensaio e a distância do eixo da centrífuga até
os extremos dos tubos em rotação é 9,0 cm.
Considerando g = 10m/s2, calcule a velocidade angular
da centrífuga para gerar o efeito de uma aceleração
gravitacional de 8,1 g.
06 - (UNESP/2008)
Em recente investigação, verificou-se que uma pequena
gota de água possui propriedades elásticas, como se
fosse uma partícula sólida. Em uma experiência,
abandona-se uma gota de uma altura h0, com uma
pequena velocidade horizontal. Sua trajetória é
apresentada na figura.
Na interação com o solo, a gota não se desmancha e o
coeficiente de restituição, definido como f, é dado pela
razão entre as componentes verticais das velocidades
de saída e de chegada da gota em uma colisão com o
solo. Calcule a altura h atingida pela gota após a sua
terceira colisão com o solo, em termos de h0 e do
coeficiente f. Considere que a componente horizontal da
velocidade permaneça constante e não interfira no
resultado.
07 - (UNESP/2007)
Em países com poucos recursos hídricos ou
combustíveis fósseis, a construção de usinas nucleares
pode ser uma alternativa para produção de energia. A
energia nuclear é obtida pela fissão de núcleos como o
de urânio e, dessa fissão, além de calor, são produzidos
nêutrons, que por sua vez serão responsáveis pela
fissão de outros núcleos de urânio. Dessa reação em
cadeia é extraída a energia nuclear.
No entanto, para uma fissão controlada, é necessário
diminuir a energia dos nêutrons que tiverem energias
cinéticas altas. Para isso, elementos moderadores são
introduzidos para que os nêutrons, em interações com
esses núcleos, tenham sua energia diminuída.
A escolha do material moderador depende de quanta
energia os nêutrons devem perder.
Considere uma colisão elástica frontal entre um nêutron
e um átomo moderador, que possua massa quatro
vezes maior que a do nêutron e esteja inicialmente em
repouso. Calcule a razão entre as energias cinéticas
final e inicial do nêutron.
08 - (UNESP/2006)
Uma esfera maciça A encontra-se em repouso na borda
de uma mesa horizontal, a uma altura h de 0,45 m do
solo. Uma esfera B, também maciça, desliza com uma
velocidade de 4,0 m/s sobre a mesa e colide
frontalmente com a esfera A, lançando-a ao solo,
conforme ilustra a figura.
Sendo uma colisão elástica, a esfera B retorna na
mesma direção de incidência com velocidade de 2,0
m/s em módulo e a esfera A toca o solo a uma distância
2h da borda da mesa. Considerando g = 10 m/s2,
calcule
a) a velocidade com que A foi lançada ao solo.
b) a razão mA / mB.
09 - (UNESP/2008)
Dois corpos, A e B, atados por um cabo, com massas
mA = 1kg e mB = 2,5kg, respectivamente, deslizam sem
atrito no solo horizontal sob ação de uma força, também
horizontal, de 12 N aplicada em B. Sobre este corpo, há
um terceiro corpo, C, com massa mC = 0,5kg, que se
desloca com B, sem deslizar sobre ele.
A figura ilustra a situação descrita.
barco a vela. Considere uma situação em que um barco
de 100 kg, conduzido por um velejador com massa de
60 kg, partindo do repouso, se desloca sob a ação do
vento em movimento uniformemente acelerado, até
atingir a velocidade de 18 km/h.
A partir desse instante, passa a navegar com
velocidade constante. Se o barco navegou 25 m em
movimento uniformemente acelerado, qual é o valor da
força aplicada sobre o barco? Despreze resistências ao
movimento do barco.
11 - (UNESP/2009)
Buriti é uma palmeira alta, comum no Brasil central e no
sul da planície amazônica. Um fruto do buriti – eles são
pequenos e têm em média massa de 30 g − cai de uma
altura de 20m e pára, amortecido pelo solo (o buriti dá
em solos fofos e úmidos). Suponha que na interação do
fruto com o solo, sua velocidade se reduza até o
repouso durante o tempo t  0, 060 s . Considerando
desprezível a resistência do ar, determine o módulo da
força resultante média exercida sobre o fruto durante a
sua interação com o solo.
Adote g = 10 m/s2.
12 - (UNESP/2008)
Um atleta, com massa de 80 kg, salta de uma altura de
3,2 m sobre uma cama elástica, atingindo exatamente o
centro da cama, em postura ereta, como ilustrado na
figura.
Devido à sua interação com a cama, ele é lançado
novamente para o alto, também em postura ereta, até a
altura de 2,45 m acima da posição em que a cama se
encontrava. Considerando que o lançamento se deve
exclusivamente à força de restituição da cama elástica e
que a interação do atleta com a cama durou 0,4 s,
calcule o valor médio da força que a cama aplica ao
atleta. Considere g = 10 m/s2.
13 - (UNESP/2009)
A figura mostra, em corte, um trator florestal
“derrubador–amontoador” de massa 13.000 kg; x é a
abscissa de seu centro de gravidade (CG). A distância
entre seus eixos, traseiro e dianteiro, é DE = 2,5m.
(J.S.S. de Lima et al. In
www.scielo.br/pdf/rarv/v28n6/23984.pdf)
Calcule a força exercida sobre o corpo C.
10 - (UNESP/2007)
Uma das modalidades esportivas em que nossos atletas
têm sido premiados em competições olímpicas é a de
Admita que 55% do peso total do trator são exercidos
sobre os pontos de contato dos pneus dianteiros com o
solo (2) e o restante sobre os pontos de contato dos
pneus traseiros com o solo (1). Determine a abscissa x
do centro de gravidade desse trator, em relação ao
ponto 1.
Adote g  10 m/s 2 e dê a resposta com dois algarismos
significativos.
14 - (UNESP/2009)
Desde maio de 2008 o IBAMA recebe imagens do
ALOS (satélite de observação avançada da Terra) para
monitorar o desmatamento na floresta Amazônica. O
ALOS é um satélite japonês que descreve uma órbita
circular a aproximadamente 700 km de altitude. São
dados o raio e a massa da Terra, rT  6.400 km e
M  6, 0 10 24 kg ,
respectivamente,
gravitacional, G  6, 7 10
11
e
a
constante
N  m / kg .
2
2
Determine o módulo da aceleração da gravidade
terrestre, em m/s2, na altitude em que esse satélite se
encontra.
15 - (UNESP/2008)
O período de revolução T e o raio médio r da órbita de
um planeta que gira ao redor de uma estrela de massa
m satisfazem à relação (m T2)/r3 = 4  2/G, onde G é a
constante de gravitação universal. Considere dois
planetas e suas respectivas estrelas. O primeiro, o
planeta G581c, recentemente descoberto, que gira em
torno da estrela Gliese581 e o nosso, a Terra, girando
ao redor do Sol. Considere o período de revolução da
Terra 27 vezes o de G581c e o raio da órbita da Terra
18 vezes o raio da órbita daquele planeta. Determine
qual seria a massa da estrela Gliese581 em unidades
da massa M do Sol.
16 - (UNESP/2008)
Em abril deste ano, foi anunciada a descoberta de
G581c, um novo planeta fora de nosso sistema solar e
que tem algumas semelhanças com a Terra. Entre as
várias características anunciadas está o seu raio, 1,5
vezes maior que o da Terra. Considerando que a massa
específica desse planeta seja uniforme e igual à da
Terra, utilize a lei da gravitação universal de Newton
para calcular a aceleração da gravidade na superfície de
G581c, em termos da aceleração da gravidade g, na
superfície da Terra.
17 - (UNESP/2007)
Satélites de órbita polar giram numa órbita que passa
sobre os pólos terrestres e que permanece sempre em
um plano fixo em relação às estrelas. Pesquisadores de
estações oceanográficas, preocupados com os efeitos
do aquecimento global, utilizam satélites desse tipo para
detectar regularmente pequenas variações de
temperatura e medir o espectro da radiação térmica de
diferentes regiões do planeta. Considere o satélite a 5
298 km acima da superfície da Terra, deslocando-se
com velocidade de 5 849 m/s em uma órbita circular.
Estime quantas passagens o satélite fará pela linha do
equador em cada período de 24 horas.
Utilize a aproximação   3,0 e suponha a Terra
esférica, com raio de 6 400 km.
18 - (UNESP/2006)
Uma pessoa, com o objetivo de medir a pressão interna
de um botijão de gás contendo butano, conecta à
válvula do botijão um manômetro em forma de U,
contendo mercúrio. Ao abrir o registro R, a pressão do
gás provoca um desnível de mercúrio no tubo, como
ilustrado na figura.
Considere a pressão atmosférica dada por 10 5 Pa, o
desnível h = 104 cm de Hg e a secção do tubo 2 cm2.
Adotando a massa específica do mercúrio igual a 13,6
g/cm3 e g = 10 m/s2, calcule
a) a pressão do gás, em pascal.
b) a força que o gás aplica na superfície do mercúrio
em A.
(Advertência: este experimento é perigoso. Não
tente realizá-lo.)
19 - (UNESP/2007)
Os tripulantes de um navio deparam-se com um grande
iceberg desprendido das geleiras polares como
conseqüência do aquecimento global. Para avaliar o
grau de periculosidade do bloco de gelo para a
navegação, eles precisam saber qual é a porção
submersa do bloco.
Experientes em sua atividade, conseguem estimar a
fração submersa do volume utilizando as massas
específicas do gelo, igual a 0,92 g/cm 3, e da água
salgada, igual a 1,03 g/cm3. Qual foi o valor da fração
submersa calculada pelos navegantes?
20 - (UNESP/2008)
Um garoto de 24 kg vê um vendedor de bexigas infladas
com gás hélio e pede à mãe 10 delas. A mãe compra
apenas uma, alegando que, se lhe desse todas, o
menino seria erguido do solo por elas. Inconformado
com a justificativa, o menino queixa-se à sua irmã, que
no momento estudava empuxo, perguntando-lhe qual
seria o número máximo daquelas bexigas que ele
poderia segurar no solo. Considerando o volume médio
de cada bexiga, 2 litros, estime o número mínimo de
bexigas necessário para levantar o garoto. Em seus
cálculos, considere a massa específica do ar igual a 1,2
kg/m3, 1 litro = 10–3m3 e despreze as massas do gás e
das bexigas.
21 - (UNESP/2009)
O Landsat 7 é um satélite de sensoriamento remoto que
orbita a 700 km da superfície da Terra. Suponha que a
menor área da superfície que pode ser fotografada por
esse satélite é de 30 m x 30m , correspondente a um
pixel, elemento unitário da imagem conjugada no sensor
óptico da sua câmara fotográfica.
A lente dessa câmara tem distância focal f = 5,0cm.
Supondo que os pixels sejam quadrados, qual o
comprimento dos lados de cada quadrado?
O ângulo de incidência i é 30º e r é um ângulo que
22 - (UNESP/2009)
Desde maio de 2008 o IBAMA recebe imagens do
ALOS, um satélite japonês de sensoriamento remoto
que orbita a cerca de 700 km da superfície da Terra.
Suponha que o sistema óptico desse satélite conjugue
imagens nítidas no seu sensor quando este se localiza
4,0 cm atrás da lente (objetiva) e seja capaz de
fotografar áreas quadradas do solo com, no mínimo,
900 m2, correspondente a um pixel (elemento unitário
de imagem) do sensor óptico da câmara. Qual a
distância focal dessa lente e a área de cada pixel sobre
a qual a imagem da superfície da Terra é conjugada?
23 - (UNESP/2008)
Uma lupa utilizada para leitura é confeccionada com
uma lente delgada convergente, caracterizada por uma
distância focal f. Um objeto é colocado a uma distância
0,8 f, medida a partir da lente. Se uma letra de um texto
tem altura 1,6 mm, determine o tamanho da letra
observado pelo leitor.
24 - (UNESP/2009)
A figura representa o gráfico do desvio ( ) sofrido por
um raio de luz monocromática que atravessa um prisma
de vidro imerso no ar, de ângulo de refringência A = 50º,
em função do ângulo de incidência 1 .
permite a aproximação sen r = tg r .
Determine o tamanho da imagem I, considerando o
índice de refração do vidro como sendo 1,7 e do ar
como 1,0.
26 - (UNESP/2009)
Em um acampamento, um grupo de estudantes coloca
0,50 L de água, à temperatura ambiente de 20 ºC, para
ferver, em um lugar onde a pressão atmosférica é
normal.
Depois de 5,0 min, observam que a água começa a
ferver, mas distraem-se, e só tiram a panela do fogão
depois de mais 10 min, durante os quais a água
continuou fervendo. Qual a potência calorífica do fogão
e o volume de água contido na panela ao final desses
15 min de aquecimento?
Despreze o calor perdido para o ambiente e o calor
absorvido pelo material de que é feita a panela;
suponha que o fogão forneça calor com potência
constante durante todo tempo.
Adote para a densidade da água:  água  1,0  kg / L .
São dados:
calor específico da água: c água  4, 2 10 3 J/(kgº C) ;
calor
latente
de
vaporização
da
água:
L água  2,3  10 J/kg .
6
Dê a resposta com dois algarismos significativos.
É dada a relação   1   2  A , em que 1 e  2 são,
respectivamente, os ângulos de incidência e de
emergência do raio de luz ao atravessar o prisma (pelo
princípio da reversibilidade dos raios de luz, é
indiferente qual desses ângulos é de incidência ou de
emergência, por isso há no gráfico dois ângulos de
incidência para o mesmo desvio  ).
Determine os ângulos de incidência
( 1 )
e de
emergência (  2 ) do prisma na situação de desvio
mínimo, em que  min  30º .
25 - (UNESP/2008)
Um objeto O é colocado frente a um corpo com
superfície esférica e uma imagem I desse objeto é
criada a uma distância de 14 cm do vértice V da
superfície, como ilustrado na figura.
27 - (UNESP/2008)
Ao ser anunciada a descoberta de novo planeta em
torno da estrela Gliese581 e a possível presença de
água na fase líquida em sua superfície, reavivou-se a
discussão sobre a possibilidade de vida em outros
sistemas. Especula-se que as temperaturas na
superfície do planeta são semelhantes às da Terra e a
pressão atmosférica na sua superfície é estimada como
sendo o dobro da pressão na superfície da Terra. A
essa pressão, considere que o calor latente de
vaporização da água no novo planeta seja 526 cal/g e a
água atinja o ponto de ebulição a 120 ºC. Calcule a
quantidade necessária de calor para transformar 1 kg de
água a 25 ºC totalmente em vapor naquelas condições,
considerando o calor específico da água 1 cal/g.
28 - (UNESP/2007)
Antibióticos podem ser produzidos induzindo o
crescimento de uma cultura de microorganismos em
meios contendo nutrientes e oxigênio. Ao crescerem,
esses microorganismos respiram e, com a oxigenação,
retiram energia dos alimentos, que em parte será
utilizada para a sua sobrevivência, e a restante liberada
na forma de energia térmica. Quando os antibióticos
são produzidos em escala industrial, a cultura de
microorganismos se faz em grandes tanques,
suficientemente
oxigenados,
conhecidos
como
biorreatores. Devido ao grande volume de nutrientes e
microorganismos, a quantidade de energia térmica
liberada por unidade de tempo neste processo aeróbico
é grande e exige um sistema de controle da
temperatura para mantê-la entre 30 ºC e 36 ºC. Na
ausência desse controlador, a temperatura do meio
aumenta com o tempo. Para estimar a taxa de
aquecimento nesse caso, considere que a cada litro de
O2 consumido no processo aeróbico sejam liberados
aproximadamente 48 kJ de energia térmica. Em um
tanque com 500 000 litros de cultura, que pode ser
considerado como meio aquoso, são consumidos 8 750
litros de O2 a cada minuto. Se o calor específico da
água é 4,2 J/(g ºC), calcule a variação da temperatura
do meio a cada minuto do processo.
29 - (UNESP/2006)
Um aquecedor elétrico fechado contém inicialmente 1
kg de água a temperatura de 25ºC e é capaz de
fornecer 300 cal a cada segundo. Desconsiderando
perdas de calor, e adotando 1 cal/(gºC) para o calor
específico da água e 540 cal/g para o calor latente,
calcule
a) o tempo necessário para aquecer a água até o
momento em que ela começa a evaporar.
b) a massa do vapor formado, decorridos 520 s a
partir do instante em que o aquecedor foi ligado.
30 - (UNESP/2007)
É largamente difundida a idéia de que a possível
elevação do nível dos oceanos ocorreria devido ao
derretimento das grandes geleiras, como conseqüência
do aquecimento global. No entanto, deveríamos
considerar outra hipótese, que poderia também
contribuir para a elevação do nível dos oceanos. Tratase da expansão térmica da água devido ao aumento da
temperatura. Para se obter uma estimativa desse efeito,
considere que o coeficiente de expansão volumétrica da
água salgada à temperatura de 20 ºC seja 2,0 x 10 4
ºC1. Colocando água do mar em um tanque cilíndrico,
com a parte superior aberta, e considerando que a
variação de temperatura seja 4 ºC , qual seria a
elevação do nível da água se o nível inicial no tanque
era de 20 m? Considere que o tanque não tenha sofrido
qualquer tipo de expansão.
31 - (UNESP/2009)
As figuras mostram uma versão de um experimento –
imaginado pelo filósofo francês René Descartes e
bastante explorado em feiras de ciências – conhecido
como ludião: um tubinho de vidro fechado na parte
superior e aberto na inferior, emborcado na água
contida em uma garrafa PET, fechada e em repouso. O
tubinho afunda e desce quando a garrafa é comprimida
e sobe quando ela é solta.
Na figura 1, o ludião está em equilíbrio estático, com um
volume aprisionado de ar de 2,1 cm 3, à pressão
atmosférica p 0  1,0 10 5 Pa . Com a garrafa fechada e
comprimida, é possível mantê-lo em equilíbrio estático
dentro d’água, com um volume de ar aprisionado de 1,5
cm3 (figura 2).
Determine a massa do tubinho e a pressão do ar
contido no ludião na situação da figura 2. Despreze o
volume deslocado pelas paredes do tubinho; supõe-se
que a temperatura ambiente permaneça constante.
Adote, para a densidade da água,  água  1,0 g/cm 3 .
32 - (UNESP/2007)
Um mol de gás monoatômico, classificado como ideal,
inicialmente à temperatura de 60 º, sofre uma expansão
adiabática, com realização de trabalho de 249 J. Se o
valor da constante dos gases R é 8,3 J/(mol K) e a
energia interna de um mol desse gás é (3/2)RT, calcule
o valor da temperatura ao final da expansão.
33 - (UNESP/2008)
Um cubo de gelo com massa 67 g e a –15 ºC é
colocado em um recipiente contendo água a 0 ºC.
Depois de um certo tempo, estando a água e o gelo a 0
ºC, verifica-se que uma pequena quantidade de gelo se
formou e se agregou ao cubo. Considere o calor
específico do gelo 2 090 J/(kg.ºC) e o calor de fusão
33,5 x 104 J/kg. Calcule a massa total de gelo no
recipiente, supondo que não houve troca de calor com o
meio exterior.
34 - (UNESP/2007)
A relação entre calor e outras formas de energia foi
objeto de intensos estudos durante a Revolução
Industrial, e uma experiência realizada por James P.
Joule foi imortalizada. Com ela, ficou demonstrado que
o trabalho mecânico e o calor são duas formas
diferentes de energia e que o trabalho mecânico poderia
ser convertido em energia térmica.
A figura apresenta uma versão atualizada da máquina
de Joule. Um corpo de massa 2 kg é suspenso por um
fio cuidadosamente enrolado em um carretel, ligado ao
eixo de um gerador.
O gerador converte a energia mecânica do corpo em
elétrica e alimenta um resistor imerso em um recipiente
com água. Suponha que, até que o corpo chegue ao
solo, depois de abandonado a partir do repouso, sejam
transferidos para a água 24 J de energia térmica.
Sabendo que esse valor corresponde a 80% da energia
mecânica, de qual altura em relação ao solo o corpo foi
abandonado? Adote g = 10 m/s2.
35 - (UNESP/2010)
Considere o gráfico da Pressão em função do Volume
de certa massa de gás perfeito que sofre uma
transformação do estado A para o estado B. Admitindo
que não haja variação da massa do gás durante a
transformação, determine a razão entre as energias
internas do gás nos estados A e B.
12) Gab: Fe = 3 800 N
13) Gab: x=1,4 m
14) Gab:8,0 m/s2
M
15) Gab: m gliese 
8
16) Gab: gG581c = 1,5
17) Gab: Assim, o satélite passará 14 vezes pela linha do
Equador a cada 24 horas.
18) Gab:
a) p = 2,4.105 Pa
b) F = 48 N
19) Gab:VLD = 0,89 Vc
20) Gab: n = 10 000 bexigas
21) Gab: 2,1 .10 -6 m
22) Gab: f=4cm; A=2,9 . 10–12 m2
23) Gab: y’ = 8 mm
24) Gab: 1  2  40º
25) Gab: |y’| = 4,1 cm
26) Gab: p  5, 6 .10 2 W; V  0,35
36 - (UNESP/2009)
As constantes termodinâmicas da
variáveis e dependem de inúmeros
condutividade térmica (km), um
k m  0,15 W/(mº C) , para madeiras
madeira são muito
fatores. No caso da
valor aceitável é
com cerca de 12%
de umidade. Uma porta dessa madeira, de espessura
d  3,0 10 -2 m e área S  2,0 m 2 , separa dois ambientes
a temperaturas de 20 ºC e 30 ºC. Qual o intervalo de
tempo necessário para que 300 J de calor atravessem
essa porta, de um ambiente para outro, supondo que,
durante a transferência de calor, as temperaturas dos
ambientes não se alterem?
Expressão do fluxo de calor, em unidades do
Q ST
SI :

k , onde t é o tempo e T é a variação
t
d
de temperatura.
GABARITO:
1) Gab:
s
4
h
2) Gab:
a) t = 0,6 s
b)   450
3) Gab:
a)
  1,5 m/s 2
b)
  0,1
4) Gab:
rad
s
6) Gab: h = f6.h0
E
9
7) Gab: f 
E i 25
5) Gab:   30
8) Gab:
a) VA= 3 m/s
mA
2
b)
mB
9) Gab: RC = 15 N
10) Gab: R = 80 N
11) Gab: 10 N
27) Gab: Q = 6,2 x 105 cal
28) Gab:
  0,20
0
C
min
29) Gab:
a) t  250 s
b) mv = 150 g
30) Gab: h  1,6 10 2 m
31) Gab: m  1,5 g;   1,4 . 105 Pa
32) Gab:TF = 313 K = 40º C
33) Gab: m = 73,27 g
34) Gab:h = 1,5 m
U
4
35) Gab: A 
UB 3
36) Gab: t  3s