Unidade 14 - Proposta de plano de estudo

Unidade 14 – Proposta de plano de estudo
Fenómenos que envolvem campos electromagnéticos variáveis
1. Indução electromagnética.
Um condutor está em equilíbrio electrostático se nele não existir movimento ordenado de cargas
eléctricas.
Conceitos
ler
pp.
exercícios
pp.
Fluxo magnético através de uma
superfície plana, ;
Variação de fluxo magnético, 
1.1.
271-272
1.
2.
274
f.e.m. induzida, 
1.2.
273
275-277
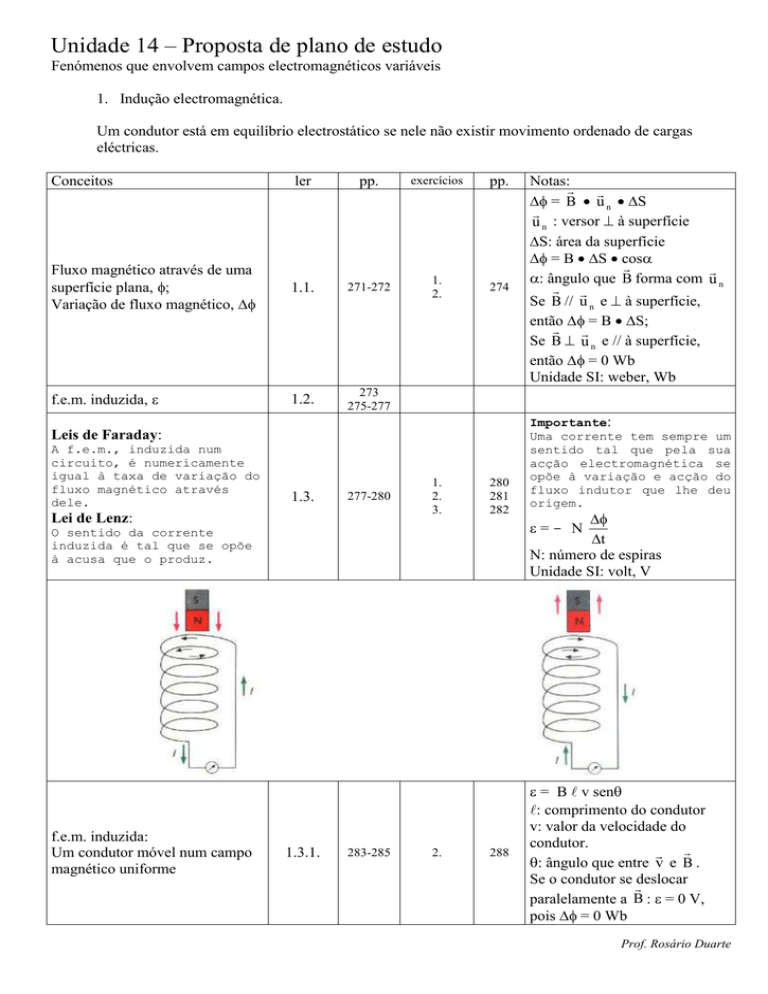
Leis de Faraday:
A f.e.m., induzida num
circuito, é numericamente
igual à taxa de variação do
fluxo magnético através
dele.
1.3.
277-280
Lei de Lenz:
1.
2.
3.
280
281
282
Importante:
Uma corrente tem sempre um
sentido tal que pela sua
acção electromagnética se
opõe à variação e acção do
fluxo indutor que lhe deu
origem.

t
N: número de espiras
Unidade SI: volt, V
=- N
O sentido da corrente
induzida é tal que se opõe
à acusa que o produz.
f.e.m. induzida:
Um condutor móvel num campo
magnético uniforme
Notas:


 = B  u n  S

u n : versor  à superfície
S: área da superfície
 = B  S  cos


: ângulo que B forma com u n
 
Se B // u n e  à superfície,
então  = B  S;
 
Se B  u n e // à superfície,
então  = 0 Wb
Unidade SI: weber, Wb
1.3.1.
283-285
2.
288
 = B  v sen
: comprimento do condutor
v: valor da velocidade do
condutor.
 
: ângulo que entre v e B .
Se o condutor se deslocar

paralelamente a B :  = 0 V,
pois  = 0 Wb
Prof. Rosário Duarte
Recordar:

 
Lei de Laplace: Fm  I    B

 
Fm  I   B sen 
I – intensidade da corrente
f.e.m. induzida:
Um condutor estacionário num
campo eléctrico associado a um
campo magnético variável no
tempo
1.3.2.
285
3.
4.

  - vector deslocamento da carga
289
eléctrica no interior do fio condutor,
mas no sentido convencional

  - valor do deslocamento das
cargas, que é o comprimento do fio
condutor
 - ângulo formado entre o fio

condutor e o B .
Lei de Lenz como consequência
da Lei da conservação de energia
1.4.
290-291
I 2
I
e 2 = - M 1
t
t
M: indução mútua dos dois
circuitos ou coeficiente de
indução mútua (constante de
proporcionalidade); depende do
meio e da distância entre os
rolamentos.
Unidade SI de L: henry, H
M > 0; M é tanto maior quanto
maior for o n.º de espiras
constituintes dos dois circuitos.
I
t
L=-
=-L
I
t
L: indutância ou coeficiente de
auto-indução (constante de
proporcionalidade).
Unidade SI de L: henry, H
1 = - M
Indução mútua
1.5.
291-292
1.
296
Auto-indução
1.6
292-294
2.
296
1.7.
294-296
1.8.
297-298
1.9.
298-299
Efeitos de auto-indução e de
indução mútua
Materiais paramagnéticos,
diamagnéticos e ferromagnéticos
Correntes de Foucault
Actividades de aplicação, pp. 301, exercícios 1., 2. e 3.
Prof. Rosário Duarte
2. Corrente altenada sinusoidal.
Conceitos
ler
pp.
exercícios
pp.
f.e.m. induzida numa espira
(f.e.m. alternada sinusoidal)
2.1.
302-303
2.
3.
4.
306
Corrente alternada sinusoidal
2.2.
304-305
1.
5.
305
307
Efeitos da corrente alternada
2.3.
308
Intensidade e ddp eficazes
(Ie e Ve)
2.4.
309
1.
2.
315
315
Notas:
 = Em sen[(2 /T)t]
Em – f.e.m. máxima
Em = B s 
B – valor do campo magnético
s – área de superfície da espira
 - velocidade angular da espira
Unidade SI: rad s-1
 = 2 /T
T = 1/f
T – período da espira, ie, tempo
que demora a dar uma volta;
Unidade SI: s, segundo
F – frequência ; número de
voltas dadas por unidade de
tempo. Unidade: Hz, hertz
I = Im sen[(2 /T)t]
Im – valor máximo da
intensidade da corrente;
Notas:
1. Corrente contínua: corrente
com um só sentido e de valor
constante;
2. corrente alternada: corrente
electrica que periodicamente
muda de sentido e cujo valor
varia entre +Im e -Im.
Efeito térmico
Efeito químico
Efeito magnético
I
Ie = m
2
Ie – é a intensidade de uma
corrente contínua constante que,
na mesma resistência e nas
mesmas condições, origina a
mesma quantidade de calor que
a corrente alternada.
V
Ve = m
2
Ve – para um circuito
constituído por uma resistência
puramente óhmica e para as
frequências normais, é o valor
de uma tensão constante que
durante o mesmo tempo fosse
aplicada aos terminais da
referida resistência e nela
libertasse a mesma quantidade
de calor.
Prof. Rosário Duarte
V = Vm sen ( t)
I = Im sen (  t + )
ddp em circuitos de corrente
alternada
2.5.
310
Circuito puramente óhmico
2.5.1.
310-311
Circuito puramente indutivo
2.5.2.
311-313
2.
323
Circuito puramente capacitivo
2.5.3.
313-314
3.
324
 - ângulo de fase ou diferença
de fase;
- Se V e I atingem o valor
máximo ou se anulam no
mesmo instante, diz-se que
estão em fase ( = 0º)
Rcontinua  Ralternada para correntes
alternadas de baixa frequência
V
R= e
Ie
I e V estão em fase
V = Vm sen ( t)
I = Im sen ( t)
Notas:
- a tensão aplicada tem de
superar a f.e.m. de auto-indução
da bobina

- I está atrasada
rad em
2
relação à tensão.
- em corrente alternada (C.A.) a
influência do coeficiente de
auto-indução manifesta-se
permanentemente, o que não
acontece com C.C. em que os
termómetros de auto-indução só
aparecem na abertura e fecho do
circuito.
- verifica-se um aumento
aparente da resistência:
reactância indutiva, XL.
XL =  L = 2  f L
Unidade SI: ohm, 

V = Vm sen ( t +
)
2
V = R I  Vm = XL Im =  L Im
Então:

V =  L Im sen ( t +
)
2
I = Im sen ( t)
O movimento dos electrões
encontra uma certa resistência
ao entrar e ao sair das
armaduras e a este efeito devido
ao condensador dá-se o nome
de efeito das armaduras e a este
efeito devido ao condensador
dá-se o nome de efeito
capacitivo. Designa-se este
efeito por reactância capacitiva,
Xc.
Prof. Rosário Duarte
1
; Unidade SI: ohm, 
C
V
V = R I  Im = m  Vm  C
Xc
V = Vm sen ( t)

I = Vm  C sen ( t + )
2
Xc =
RESUMO:
V
V = Vm sen ( t)
V =  L Im sen ( t +
Resistência
Circuito puramente óhmico:
V
R= e
Ie
Circuito puramente indutivo:
XL =  L
Circuito puramente capacitivo:
1
Xc =
C
I
I = Im sen ( t)

)
2
V = Vm sen ( t)
I = Im sen ( t)
I = Vm  C sen ( t +

)
2
Z: impedância do circuito
Unidade SI: ohm, 
Z=
R 2  (X L  X C ) 2
V
V
ou Z = e
I
Ie
Em série :
V = VR + VL + VC
VR = R I
VL = X L I
VC = Xc I
Z=
Impedância (Lei de Ohm aplicada
a um circuito de c.a.)
2.6.
316-319
4.
5.
325
1
,
C
então Z = R, diz-se que há
ressonância; isto acontece para:
1
1
L=
f=
C
2 LC
Potência útil - potência média
de um circuito:
P = Ve Ie cos 
Unidade SI: watt, W
Circuito puramente indutivo:

=
P=0W
2
Circuito puramente capacitivo:

=
P=0W
2
Potência aparente – é o produto
dos valores eficazes da tensão e
da intensidade da corrente.
S = Ve Ie
Unidade SI: volt-ampére, VA
Se XL = Xc   L =
Potência média em circuito de
corrente alternada sinusoidal:
Potência real (útil)
Potência aparente, S
2.7.
320-321
321
6.
7.
8.
9.
326331
Prof. Rosário Duarte
Factor de potência
322
Potência reactiva, Q
322
Factor de potência: cos 
Q = Ve Ie sen 
Unidade SI: volt-ampére
reactivo, VAr
Relações matemáticas:
Transformadores estáticos e seu
funcionamento:
2.8.
331
Razão da transformação de um
transformador, rt
2.8.1.
333
1.
2.1.
335
336
Transformadores em vazio
2.8.2.
334
2.
336
Transformadores em carga
2.8.2.
334
Rendimento de um transformador
2.8.2.
334
2.2.
336
Vantagens em transportar energia
eléctrica (c.a.) a alta tensão.
Aplicações dos transformadores
2.8.3.
337
S = P2  Q2
P = S cos 
Q = S sen 
Transformador – aparelho que
modifica ou transforma
simultaneamente a tensão e a
intensidade de uma corrente
eléctrica.
Constituição: p. 331.
Funcionamento: p. 332.
rt - quociente entre a tensão
mais elevada e a tensão mais
baixa. Por exemplo:
V
N
rt = 2 = 2 (transformador
V1
N1
elevador de tensão)
N1 e N2 – n.º de espiras do
primário e do secundário.
Se N1 < N2, há aumento de
tensão nos terminais do
secundário devido ao n.º de
espiras que constituem este
enrolamento;
Se N1 > N2, há diminuição de
tensão nos terminais do
secundário.
Se V2>V1 o transformador
funciona como elevador de
tensão.
Se V2<V1 o transformador
funciona como abaixador de
tensão.
Um transformador está em
vazio, quando o circuito do
secundário está interrompido: a
corrente neste enrolamento é
nula e a potência é igualmente
nula.
Verifica-se: cos 1 = cos 2
V1I1 = V2I2
P
= 2
P1
Actividades de aplicação, pp. 399-342.
Prof. Rosário Duarte