Apresentação do PowerPoint

UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO
INSTITUTO POLITÉCNICO
Graduação em Engenharia Mecânica
Disciplinas:
Mecânica dos Materiais 2 – 6º Período
E
Dinâmica e Projeto de Máquinas 2-10º Período
Professor: Dr. Damiano da Silva Militão.
Tema de aula 7: Teoria das Falhas
OBJETIVO:
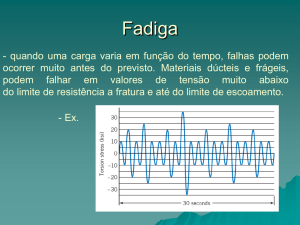
Estabelecer os limites de tensão para falha dos materiais dúcteis ou frágeis,
imóveis e sob carregamento constantes, através de teorias baseadas nas tensões
principais.
SEQUÊNCIA DE ABORDAGENS:
7.1-Materiais Dúcteis;
-Teoria da tensão de cisalhamento máxima
-Teoria da Energia de distorção máxima.
7.2-Materiais Frágeis;
-Teoria da tensão normal máxima
-Critério de falha de Mohr
7.3-Mecânica da Fratura.
7.1-Materiais Dúcteis.
Teoria da tensão cisalhante máxima (ou critério de escoamento de Tresca);
“Dúcteis falham por escoamento, deslizando planos cristalinos devido ao cisalhamento.”
Imagine um corpo de prova (em formato de tira fina) sob tração;
Teremos estes planos à 45º do eixo.
Na tensão axial limite de escoamento σE para um elemento da superfície ,
por Mohr a tensão cisalhante máxima seria;
Multiaxialmente, esta teoria diz que o escoamento inicia quando
atinge este
.
Vimos em 1.6 que;
Se σ1 e σ2 tem mesmo sinal->
= max|σ1ou2|/2 (fora do plano)
Se σ1 e σ2 tem sinais diferente->
Fazendo
=
= (σ1-σ2)/2 (no plano)
para os dois casos, teremos;
GRAFICAMENTE;
NA REGIÃO FORA DA ÁREA HEXAGONAL
O MATERIAL ESCOARÁ.
Teoria da energia de distorção máxima (ou de von Mises e H. Hencky);
Vimos em 6.1 (eq. (18)) que a energia de deformação no estado multiaxial é dada por;
Logo p/ um elem. cúbico com E,ν, σ1, σ2
e σ3 ctes, dividindo por V temos a
densidade de energia de deformação:
Que se separa em 2 componentes:
u é devido à σ =σ =σ =σ (só muda volume,
u=uh+ud
(hidrostática + distorção)
buscamos
ud = u – uh
Substituindo u, uh ,e σ h= (σ1+σ2+σ3 )/3;
h
h
1
2
3
ñ a forma) ; uh =(1/2E)(3 σh2 – 2.ν.3 σh2 )
ud é devido à distorção (só muda forma e dá
uma dimensão do cisalhamento)
no estado plano com σ3=0;
ou num teste uniaxial σ1=σE, σ2=σ3=0;
Esta teoria compara ud do estado multiaxial, com (ud)E uniaxial buscando a tensão uniaxial equivalente de
von Mises (σ’) que causaria a mesma en. de deformação multiaxial.
Igualando no estado triplo;
σ'
igualando no estado biaxial;
Graficamente temos;
σ'
Estado triplo; σ'
(cilindro inclinado)
Estado biaxial;
σ'
(elipse)
Comparação dos critérios de falha dúcteis;
• Observe que a Teo. da máxima def. por cis. é mais conservadora.
• Observe que com cisalhamento puro (só torção) (σ1e σ2 à 45º de
τ, com σ1=τ (tração) e σ2=-τ (compressão)) temos a máxima diferença
entre as teorias.
Exemplo; O estado de tensão sobre a estrutura do assento durante uma
trombada é mostrado na figura. Determine o menor limite de escoamento para o aço a ser selecionado para o elemento, baseando-se na
teoria da tensão de cisalhamento máxima.
Sol:
Com a convenção de sinais temos
As tensões principais serão obtidas por Mohr, ou pela relação;
->Sinais contrários; pela T.M.T.C;
Da tabela, o aço
ferramenta L2 por
ex. é indicado!
Fazer; Uma liga de alumínio 6061-T6 (σE=37.103ksi) deve ser usada em um eixo de acionamento para que
transmita 40 hp (1hp=550ft.lb/s) à 2.400 rev/min.Usando um fator de segurança F.S. = 2, em relação ao escoamento, determine o menor diâmetro do eixo com base na teoria da energia de distorção máxima.
7.2-Materiais Frágeis.
Teoria da tensão normal máxima; (p/materiais uniformes)
“Frágeis falham por fratura devido à tração, (sem escoar) ao atingir σr(lim. resist.)”
σr será aproximadamente a mesma tanto em ensaio de tração simples (σ1=σr),
quanto em ensaio de torção (σ1=σr à 45º);
Graficamente;
Obs: Em uniformes diag. σ-ε para tração
e compressão tem mesmos valores;
Critérios de falha de Mohr; (p/ ñ uniformes)
Analisamos σr nos testes de;
tração (σr)t ,
compressão (σr)c e
torção τr;
A região dentro do envelope tg aos círculos
será segura,
Experimentalmente comprova-se que a mais indicada é a Teo.
de Coulumb Mohr modificada. Ela tb utiliza uma tensão
equivalente uniaxial;
(em analogia à von Mises),
Onde;
Esta região é representada graficamente
pelas 3 novas teorias abaixo;
Exemplo; O pequeno cilindro de concreto com diâmetro de 50mm está sujeito a um torque de
500 N.m e a uma força de compressão axial de 2 kN. Determinar se ele falhará de acordo com
a teoria da tensão normal máxima. O limite de resistência do concreto é σr =28 MPa.
Sol: A T.T.N.M exige verificar se σ1 e σ2 < σr para não falhar;
Propriedades da seção;
O estado de tensão terá;
E as tensões principais;
Como
28MPa, e
28MPa o critério é satisfeito.
Fazer; Determine o F.S para a haste. Use a Teo.de Mohr Modif. nos pts
críticos A e B. Dados; (σr)t =52500psi, (σr)c =-164000psi, L=6in, a=8in e d=1,5 in.
F=1000lb
7.3-Mecânica da Fratura.
Consideramos até aqui materiais homogêneos e isotrópicos, sem fendas, lacunas ou inclusões.
Trincas causam tensão concentrada (numa direção θ e posição r) em suas extremidades (Ex. Trinca de borda),
Isso pode causar falha brusca mesmo em materiais dúcteis:
Teoria da mecânica da fratura linear elástica(MFLE);
Consideramos a MFLE que pressupõe;
Pequena região de escoamento plástico próximo à ponta, se comparada
com a região elástica do restante do corpo.
Modos geométricos de trinca:
Trabalharemos no modo (I)
Puxa
Desliza
Rasga
Fator de intensidade de tensão (KIII, KII ou KI(trabalhado)):
Para trincas agudas e b>>a, calcula-se tensão de von Mises (σ’) em função de θ teremos: Ex. para r=10-6in;
teremos θmáx=+- 81º.
Mantendo θ máx =81º e plotando σ’ em função de r temos;
Observa-se que próximo à ponta (r->0 ) temos σ’->máx.
Nessa região a tensão é diretamente prop. à K;
Onde:
• σnom é a T. nominal (despreza comprimento da trinca(menos preciso)).
• β varia p/ geometria, carga, (a/b) e tipo; Ex: -Trinca central;
(ou ϐ=1 com Erro<10% para a/b<0,4)
-Trinca de borda ou ambas as bordas ou de borda sob flexão;
(Erro<10% para a/b<0,13 ou a/b<0.6 ou a/b<0,4 respetivamente)
Tenacidade à fratura (Kc )ou (KIc):
Propriedade do material obtida experimentalmente (varia como a ductilidade);
Propagação súbita se K>=Kc
Trinca Estável se K<Kc (Fator de segurança F.SFM=Kc/K)
Exemplo; Uma tira de aço projetada para suportar 60000 N de tração axial foi acidentalmente talhada em sua
borda. Determine (a)o coeficiente de segurança da tira original, sem trinca, baseado no escoamento, e (b)seu
novo coeficiente de segurança "trincado" baseado na mecânica da fratura. (c) Quão grande a trinca poderia
ficar antes da falha? Dados σE=540MPa e Kc=66MPa.m0,5,comprimento L =6 m, largura b=80mm e espessura
t=3 mm. O comprimento da trinca a=10mm, paralela à espessura.
Sol: (a)
Então teremos a tensão equivalente de von Mises;
Logo pela T. da energia de distorção temos:
σ'
F.S=σE/σ’
(b) a/b é < 0,13 permitindo usar
Logo;
Para que a trinca esteja estável precisamos K<Kc
Logo;
F.SFM=66/49,63=1,33
(Fator de segurança F.SFM=Kc/K)
(c) O tamanho ‘a’ máximo da trinca pode ser aproximada usando;
a trinca se propaga se; F.SFM>=1 (ou seja, K=Kc );
66/(1.12(250)
a=0.017m ou 17mm é o tamanho aproximado máximo da trinca sem falha!
– Bibliografia:
– R. C. Hibbeler – Resistência dos materiais – 5º Edição.
– Robert L. Norton – Projeto de máquinas, uma abordagem integrada.
MUITO OBRIGADO PELA ATENÇÃO!