Matemática Financeira - Professor Hubert Chamone Gesser, Dr.

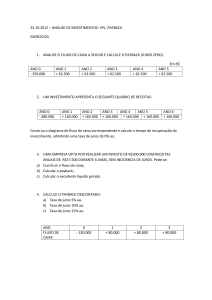
Disciplina
Orçamento Empresarial
Análise de Investimentos
(Payback, VPL e TIR)
1
Payback Simples
Prof. Hubert Chamone Gesser, Dr.
Retornar
2
Payback
DEFINIÇÃO DE PAYBACK
Pode ser entendido como o tempo exato de retorno necessário
para se recuperar um investimento inicial.
É uma técnica de análise de investimentos.
Se o PAYBACK FOR MENOR que o período máximo aceitável
ACEITA-SE O PROJETO DE INVESTIMENTO
Se o PAYBACK FOR MAIOR que o período máximo aceitável
REJEITA-SE O PROJETO DE INVESTIMENTO
3
Payback
EXEMPLO DE PAYBACK
- Uma empresa está considerando a aquisição de um ativo no
valor de $10.000,00 que gera entradas de caixa anuais de
$4.000,00 para os próximos 5 anos (vida útil do ativo).
Determinar o payback deste projeto.
Dados:
Investimento inicial = $10.000,00
Entradas de caixa = $4.000,00
Prazo do projeto = 5 anos ou 60 meses
4
Payback
EXEMPLO DE PAYBACK
Ano
FC
Saldo
0
-10000
-10000
1
4000
-6000
2
4000
-2000
3
4000
2000
4
4000
6000
5
4000
10000
Resolução:
Aplica-se a regra de três
$4.000,00
12 meses
$10.000,00
X meses
X = 30 meses
Resposta:
O Payback será de 30 meses
(2 anos e 6 meses)
5
Payback
EXEMPLO DE PAYBACK
Dados:
Investimento inicial = $10.000,00
Entradas de caixa = $4.000,00/ano
Prazo do projeto = 5 anos ou 60 meses
$4.000
0
1
Payback
2
3
4
5 Anos
Ganho
$10.000
Resposta: O Payback será de 30 meses (2 anos e 6 meses)
6
Payback
Payback Simples - PBS
Análise do prazo de recuperação do
capital investido, sem considerar o
valor do dinheiro no tempo.
400,00
250,00
200,00
Payback
Companhia Nana Neném Ltda.
Tempo
- 500,00
Ano
FC
Saldo
0
-500
-500
1
200
-300
2
250
-50
3
400
350
Cálculo do PBS
FCs distribuído nos anos
PBS = 2 + 50/400
PBS = 2,125 anos
Payback
Vantagens do Payback Simples
• Simples
• Fácil de calcular
• Fácil de entender
Payback
Perigos do Payback Simples
• Não considera o valor do dinheiro
no tempo
Payback Descontado
• Miopia financeira
– Visão curta
– Analisa até a recuperação do capital
investido
Outras técnicas devem
ser empregadas
Payback
400,00
4.000.000.000
300,00
200,00
A miopia do payback
Aumentando o
valor ...
Tempo
- 500,00
... O Payback
não se altera!!!
Valor Presente Líquido
Prof. Hubert Chamone Gesser, Dr.
Retornar
12
Valor Presente Líquido
DEFINIÇÃO DE VPL
O VPL (Valor Presente Líquido) é o valor presente das
entradas ou saídas de caixa menos o investimento inicial.
É uma técnica de análise de investimentos.
Se o VPL > 0
ACEITA-SE O INVESTIMENTO
Taxa do Negócio > Taxa de Atratividade
Se o VPL < 0
REJEITA-SE O INVESTIMENTO
Taxa do Negócio < Taxa de Atratividade
Se o VPL = 0
O INVESTIMENTO É NULO
Taxa do Negócio = Taxa de Atratividade
13
Valor Presente Líquido
EXEMPLO DE VPL
- Um projeto de investimento inicial de $70.000,00 gera entradas
de caixa de $25.000,00 nos próximos 5 anos; em cada ano será
necessário um gasto de $5.000,00 para manutenção, considerando
um custo de oportunidade de 8% ao ano. Determine o VPL:
$20.000
$20.000
$20.000
$20.000
$20.000
1
2
3
4
5
0
anos
$70.000
f
2
REG
0
0
0
7
0
0
g
0
CFj
0
0
5
CHS
g
Nj
g
8
CF0
i
f
NPV
Resposta: VPL = $9.854,2007 (VPL > 0, logo o projeto deve ser aceito)
14
Valor Presente Líquido
Descrição do VPL
Considera a soma de TODOS os
fluxos de caixa na DATA ZERO
Valor Presente Líquido
400,00
250,00
200,00
Trazendo para o valor presente
Tempo
688,96
- 500,00
181,82
206,61
300,53
$188,96
Considerando CMPC
igual a 10% a. a.
Valor Presente Líquido
Valor Presente Líquido
VPL na HP 12C
NPV = Net Present Value
[g] [CF0]  Abastece o Fluxo de Caixa do ano 0
[g] [CFj]  Abastece o Fluxo de Caixa do ano j
Cuidado!!!
j <= 20 !!!
[g] [Nj]  Abastece o número de repetições
[i]  Abastece o custo de capital
[f] [NPV]

Calcula o VPL
Valor Presente Líquido
Calculando VPL na HP12C
Ano
FC
0
-500
1
200
2
250
3
400
[f] [Reg]
500 [CHS] [g] [CF0]
200 [g] [CFj]
250 [g] [CFj]
400 [g] [CFj]
10 [i] [f] [NPV]
$188,9557
Valor Presente Líquido
Uso do VPL
>
VPL < Zero
VPL
Zero
Aceito!!!
Rejeito!!!
Valor Futuro Líquido
Prof. Hubert Chamone Gesser, Dr.
Retornar
20
Valor Futuro Líquido
Descrição
Considera a soma de TODOS os
fluxos de caixa na DATA N
Na HP12c não é possível utilizar a função g Nj
Valor Futuro Líquido
400,00
250,00
200,00
Levando os valores para o futuro
Tempo
400,00
- 500,00
275,00
242,00
- 665,50
$251,50
Considerando CMPC
igual a 10% a. a.
VFL
Valor Futuro Líquido
Calculando VFL na HP12C
Ano
FC
0
-500
1
200
2
250
3
400
[f] [Reg]
500 [CHS] [g] [CF0]
200 [g] [CFj]
250 [g] [CFj]
400 [g] [CFj]
10 [i] [f] [NPV]
188,9557
[FV] [FV] [CHS] $251,5000
Valor Futuro Líquido
Uso do VFL
VFL
VFL
>
<
Zero
Aceito!!!
Zero
Rejeito!!!
Valor Uniforme Líquido
Prof. Hubert Chamone Gesser, Dr.
Retornar
25
Valor Uniforme Líquido
Descrição
É a soma de TODOS os fluxos de caixa
DISTRIBUÍDOS UNIFORMEMENTE
Na HP12c não é possível utilizar a função g Nj
Valor Uniforme Líquido
400,00
250,00
200,00
VUL = VPL distribuído
Tempo
- 500,00
VPL = $188,96
VUL
Para calcular os valores
costuma-se usar o
Excel ou a HP 12C
Valor Uniforme Líquido
Calculando VUL na HP12C
Ano
FC
0
-500
1
200
2
250
3
400
[f] [Reg]
500 [CHS] [g] [CF0]
200 [g] [CFj]
250 [g] [CFj]
400 [g] [CFj]
10 [i] [f] [NPV]
188,9557
[PMT] [PMT] [CHS] $75,9819
Valor Uniforme Líquido
Uso do VUL
>
VUL <
VUL
Zero
Aceito!!!
Zero
Rejeito!!!
Taxa Interna de Retorno
Prof. Hubert Chamone Gesser, Dr.
Retornar
30
Taxa Interna de Retorno
TIR
A TIR (Taxa Interna de Retorno) é a taxa de desconto que
iguala os fluxos de caixa ao investimento inicial. Em outras
palavras é a taxa que faz o VPL ser igual a “zero”.
É uma sofisticada técnica de análise de investimentos.
Se a TIR > Custo de Oportunidade
ACEITA-SE O INVESTIMENTO
Se a TIR < Custo de Oportunidade
REJEITA-SE O INVESTIMENTO
Se a TIR = Custo de Oportunidade
INVESTIMENTO NULO
31
Taxa Interna de Retorno
EXEMPLO DE TIR
- Um projeto está sendo oferecido nas seguintes condições: Um
investimento inicial de $1.000,00, com entradas de caixa mensais
de $300,00, $500,00 e $400,00 consecutivas, sabendo-se que um
custo de oportunidade aceitável é 10% ao mês. O projeto deve ser
aceito?
$300
0
1
$500
$400
2
3
CHS
g
meses
$1000
f
CFj
REG
5 0
1
0
0
g
0
0
CFj
Resposta: TIR = 9,2647% a.m.
4 0 0
CF0
3
g CFj
f
(TIR < Custo de oportunidade
0
0
g
IRR

REJEITAR)
32
Taxa Interna de Retorno
Taxa Interna
de Retorno
TIR
O quanto
ganharemos com
a operação!
Taxa Interna de Retorno
Conceitualmente ...
A TIR corresponde à rentabilidade auferida
com a operação
TIR = 35% a.a.
0
$270
1 ano
-$200
Taxa Interna de Retorno
Analisando um fluxo com ...
Muitos capitais
diferentes e com CMPC
CMPC = Custo Médio Ponderado do Capital
WACC = Weighted Average Capital Cost
Taxa Interna de Retorno
Perfil do VPL
200,00
20%
25%
30%
35%
188,96 125,96 71,76 24,80 -16,16 -52,10
Taxa Interna de Retorno
150,00
TIR = 27,95% a.a.
400,00
250,00
15%
250,00
VPL
10%
200,00
CMPC
100,00
50,00
•Tempo
(50,00) 0%
10%
20%
30%
40%
(100,00)
Relação inversa entre CMPC e VPL
- 500,00
Taxa Interna de Retorno
Conceito algébrico da TIR
Valor do CMPC que faz com que o
VPL seja igual a zero.
No exemplo anterior:
quando a TIR é de 27,95% a.a. o VPL é igual a Zero.
CMPC = Custo Médio Ponderado do Capital
Taxa Interna de Retorno
Cálculo Matemático da TIR
Solução polinomial …
200
250
400
VPL  500 


1
2
3
1  K  1  K  1  K 
VPL = 0, K = TIR
200
250
400
0  500 


1
2
3
1  TIR  1  TIR  1  TIR 
TIR é raiz do polinômio …
Taxa Interna de Retorno
HP 12C:
[ f ] [ IRR ]
Na prática
Microsoft Excel:
=TIR(Fluxos)
Taxa Interna de Retorno
TIR na HP 12C
IRR = Internal Rate of Return
[g] [CF0]  Abastece o Fluxo de Caixa do ano 0
[g] [CFj]  Abastece o Fluxo de Caixa do ano j
Cuidado!!!
j <= 20 !!!
[g] [Nj]  Abastece o número de repetições
[f] [IRR]

Calcula a TIR
Taxa Interna de Retorno
Calculando a TIR na HP12C
Ano
FC
0
-500
1
200
2
250
3
400
[f] [Reg]
500 [CHS] [g] [CF0]
200 [g] [CFj]
250 [g] [CFj]
400 [g] [CFj]
[f] [IRR] 27,9471%a.a.
Taxa Interna de Retorno
CUIDADO COM O CÁLCULO DA TIR
Alguns exemplares da Calculadora HP-12c Platinum
foram produzidos com erro! Teste o seu:
f REG 11950 CHS g CFo 4000 g CFj
3000 g CFj 5000 g CFj f IRR
Resultado correto:
Resultado incorreto:
0,200690632
1,346000-10
(pela HP-12C Platinum)
42
Taxa Interna de Retorno
Uso da TIR
TIR
TIR
>
<
CMPC
Aceito!!!
CMPC
Rejeito!!!
BIBLIOGRAFIA
ALBERTON, A.; DACOL, S. HP12-C Passo a Passo. 3.ed. Florianópolis: Bookstore,
2006.
BRUNI, A. L.; FAMÁ, R. A Matemática das Finanças: com aplicações na HP-12C e
Excel. Série desvendando as finanças. 1.ed. São Paulo: Atlas, v.1., 2003.
CASTELO BRANCO, A. C. Matemática Financeira Aplicada: Método algébrico, HP12C, Microsoft Excel. 1.ed. São Paulo: Pioneira Thomson Learning, 2005.
CRESPO, A. A. Matemática Financeira Fácil. 14.ed. São Paulo: Saraiva, 2010.
GITMAN, L. J. Princípios de Administração Financeira. 11.ed. São Paulo: Harbra,
2006.
GUERRA, F. Matemática Financeira através da HP-12C. 3.ed. Florianópolis: UFSC,
2003.
HOJI, M. Administração Financeira: Uma abordagem prática. 5.ed. São Paulo: Atlas,
2005.
PUCCINI, A.L. Matemática Financeira Objetiva e Aplicada. 7.ed. São Paulo: Saraiva,
2004.
TOSI, A. J. Matemática Financeira: com utilização da HP-12C. 1.ed. São Paulo: Atlas,
2004.
SAMANEZ, C. P.. Matemática Financeira: aplicações à análise de investimentos. 4.ed.
São Paulo: Prentice Hall, 2006.
Retornar
44