teoria-dos-conjuntos

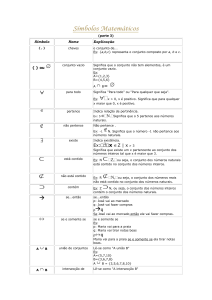
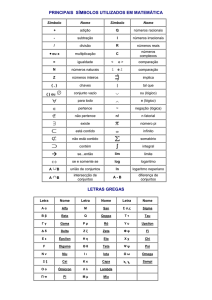
CONJUNTO
Um conjunto se pode entender como
uma coleção ou agrupamento bem
definido de objetos de qualquer classe.
Os objetos que formam um conjunto
são chamados membros ou elementos
do conjunto.
Exemplo:
Na figura ao lado temos
um Conjunto de Pessoas
NOTAÇÃO
Todo conjunto se escreve entre chaves { }
e se denota mediante letras maiúsculas A,
B, C, ..., seus elementos se separam
mediante vírgula.
Exemplo:
O conjunto das letras do alfabeto; a, b,
c, ..., x, y, z. Se pode escrever assim:
L = {a, b, c, ..., x, y, z}
Na teoria de conjuntos não precisa repetir
os elementos, por exemplo:
O conjunto {x, x, x, y, y, z } simplemente
será { x, y, z }.
O número de elementos de um conjunto A
chamamos CARDINAL DO CONJUNTO e se
representa por n(A).
Exemplo:
A = {a, b, c, d, e} seu cardinal n(A) = 5
B = {x, x, x, y, y, z} seu cardinal n(B) = 3
ÍNDICE
Para indicar que um elemento pertence a
um conjunto se usa o símbolo: 
Se um elemento não pertence a um
conjunto se usa o símbolo: 
Exemplo: Seja M = {2, 4, 6, 8, 10}
2  M 2 pertence ao conjunto M, ou seja, 2
é elemento de M.
5 M
5 não pertence ao conjunto M, ou
seja, 5 não é elemento de M.
ÍNDICE
Há duas formas de determinar um conjunto,
por Extensão e por Entendimento.
I) POR EXTENSÃO
É aquela forma mediante a qual se indica
cada um dos elementos do conjunto.
Exemplos:
A) O conjunto dos números pares maiores que
5 e menores que 20.
A = { 6, 8, 10, 12, 14, 16, 18 }
ÍNDICE
B) O conjunto de números negativos ímpares
maiores que -10.
B = {-9, -7, -5, -3, -1 }
II) POR CONDIÇÃO ou PROPRIEDADE
É aquela forma mediante a qual se dá uma
propriedade que caracteriza a todos os
elementos do conjunto.
Exemplo: P = {os números dígitos }
Se pode entender que o conjunto P está formado
pelos números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Outra forma de escrever é: P = { x / x = dígito }
se lê “P é o conjunto formado pelos
elementos x tal que x é um dígito”.
Exemplo:
Expressar por extensão e por condição ou
propriedade o conjunto de dias da semana.
Por Extensão: D = {segunda, terça, quarta,
quinta, sexta, sábado, domingo }
Por Condição ou Propriedade: D = { x / x = dia da
semana }
ÍNDICE
Os diagramas de Venn que se devem ao
filósofo inglês John Venn (1834-1883) servem
para representar conjuntos de maneira gráfica
mediante desenhos ou diagramas que podem
ser círculos, retângulos, triângulos ou
qualquer curva fechada.
V
e
o
i
(2;4)
a
u
(5;8)
(1;3) (7;6)
ÍNDICE
CONJUNTO VAZIO
É um conjunto que não tem elementos, também
se chama conjunto nulo. Geralmente se
representa pelos símbolos: ou { }
A=
ou A = { } se lê: “A é o conjunto vazio”
Exemplos:
M = { números maiores que 9 e menores que 5 }
P={x/
1
0}
X
CONJUNTO UNITÁRIO
É o conjunto que tem um só elemento.
Exemplo:
F = { x / 2x + 6 = 0 }
CONJUNTO FINITO
É o conjunto com limitado número de
elementos.
Exemplos:
E = { x / x é um número impar positivo
menor que 10 }
N = { x / x2 = 4 }
CONJUNTO INFINITO
É o conjunto com ilimitado número de
elementos.
Exemplos:
R = { x / x < 6 } ; S = { x / x é um número par }
CONJUNTO UNIVERSO
É um conjunto referencial que contém todos
os elementos de uma situação particular, se
representa pela letra U
Exemplo: O universo ou conjunto universal
de todos os números é o conjunto dos
NÚMEROS COMPLEXOS.
ÍNDICE
SUBCONJUNTO
Um conjunto A é subconjunto de B, se e somente
se, todo elemento de A for também elemento de B.
A está completamente dentro de B.
NOTAÇÃO : A  B
Lemos A está contido em B, A é subconjunto de
B.
REPRESENTAÇÃO GRÁFICA :
PROPRIEDADES:
I) Todo conjunto é subconjunto de si mesmo. A  A
II) O conjunto vazio é subconjunto de qualquer
conjunto.
Se o conjunto Vazio não é subconjunto de A, então o conjunto
vazio possui pelo menos um elemento diferente do conjunto A.
Absurdo, pois o conjunto Vazio não possui elementos. Logo o
conjunto Vazio é subconjunto de qualquer conjunto.
III) A está contido em B ( A  B ) equivale a dizer
que B contém A ( B  A )
Se A não está contido em B ou A não é subconjunto de B
significa que pelo menos um elemento de A não pertence
a B. ( A  B )
Simbolicamente:
A  B  x  A  x  B
IGUALDADE
DE CONJUNTOS
Dos conjuntos são iguais se têm os mesmos
elementos.
Exemplo:
A = { x / x2 = 9 } y B = { x / (x – 3)(x + 3) =0 }
Resolvendo a equação de cada conjunto se obtém
em ambos os casos que x é igual a 3 ou -3, ou
seja: A = {-3; 3} y B = {-3; 3}, portanto A = B
Simbolicamente : A = B
CONJUNTO DE CONJUNTOS
É um conjunto cujos elementos são conjuntos.
Exemplo:
F = { {a}; {b}; {a; b}; {a; b; c} }
Observe que os elementos do conjunto F também
são conjuntos.
{a} é um elemento do conjunto F então {a}  F
É correto dizer que {b}  F ?
NÃO
Porque {b} é um elemento do conjunto F, o
correto é {b}  F
CONJUNTO POTÊNCIA
O conjunto potência de um conjunto A denotado
por P(A) ou Pot(A) é o conjunto formado por
todos os subconjuntos de A.
Exemplo: Seja A = { m, n, p }
Os subconjuntos de A são:
{m}, {n}, {p}, {m,n}, {m,p}, {n,p}, {m,n,p}, Φ
Então o conjunto potência de A é:
P(A) = { {m}, {n}, {p}, {m, n}, {m, p}, {n, p}, {m, n, p}, Φ }
QUANTOS ELEMENTOS
POTÊNCIA DE A ?
TEM
O
CONJUNTO
Observe que o conjunto A tem 3 elementos e seu
conjunto
seja P(A) tem 8 elementos.
Se 5 potência
< x < 15 eou
é um
número par então
B = { 6, 8, 10, 12, 14 }
PROPRIEDADE:
Observe que o conjunto
Dado
um conjunto A cujo número de elementos
B tem 5 elementos então:
é n, então o número de elementos de seu
n
Card
P(B)
=
2
conjunto potência é 2n.
5 = 32
P(B)
=
2
Exemplo:
Dado o conjunto B ={ x / x é um número par e
5 < x < 15 }. Determinar o cardinal de P(B).
RESPOSTA
ÍNDICE
UNIÃO DE CONJUNTOS
A união de dois conjuntos A e B é o conjunto dos
elementos que estão em A ou em B (ou em
ambos). .
Indicamos esse conjunto por A U B
Exemplo:
A = { 2, 3, 4, 5, 8 } e B = { 1, 2, 3, 6, 7}
A U B = { 1, 2, 3, 4, 5, 6, 7, 8 }
O conjunto “A intersecção B” que se representa A  B é
o conjunto formado por todos os elementos que
pertencem a A e pertencem a B.
Exemplo:
A = {2,3,4,5,8}
B = {1,2,3,6,7}
CONJUNTOS DISJUNTOS
Dois conjuntos são disjuntos quando não têm
elementos comuns.
REPRESENTACÃO GRÁFICA :
A
B
7
5
4
9
1
3
6
2
8



Como podemos
observar os
conjuntos A e B
não têm elementos
comuns, portanto
são CONJUNTOS
DISJUNTOS
O conjunto “A menos B” que se representa A  B é o
conjunto formado por todos os elementos que pertencem
a A e não pertencem a B.
Exemplo:
A
1
3
2
4
A = {1, 2, 3, 4, 5, 6, 7}
7
6
5
A – B = { 1, 2, 3, 4}
B = {5, 6, 7, 8, 9}
7
5
8
6
9
B
Outro exemplo usando o diagrama de Venn
Números Naturais (N) N = {1; 2; 3; 4; 5; ....}
Números Inteiros (Z)
Z = {...; -2; -1; 0; 1; 2;....}
Números Racionais (Q)
1
Q = {...; -2; -1;  ; 0; 1 ;
2
5
Números Irracionais ( I )
1
;
2
1;
4
3
; 2; ....}
I = {...;
2; 3;;....}

Números Reais ( R )
R = {...; -2; -1; 0; 1; 2; 3 ; 2; 3; ....}
Números Complexos ( C )
1

C = {...; -2; 2 ; 0; 1; 2; 3 ; 2 + 3i; 3; ....}
C
R
Z
N
Q
I
PROPRIEDADES DA UNIÃO DE
CONJUNTOS
1. A U A = A
2. A U B = B U A
3. A U Φ = A
4. A U U = U
5. (AUB)UC = AU(BUC)
6. Se A U B = Φ  A = Φ e B = Φ
ÍNDICE
P={3}
EXEMPLOS:
Expressar por extensão os seguintes conjuntos:
Q={-3;3}
A ) P  x  N / x 2  9  0
F={}
B ) Q  x  Z / x  9  0
C ) F  x  R / x 2  9  0
2

E ) B  x  I /(3x  4)(x 
D ) T  x  Q /(3x  4)(x  2)  0
2)  0
4
T 

3
B
2 
RESPOSTAS
INDICE
Dado um conjunto universo U e um conjunto
A, se chama complemento de A ao conjunto
formado por todos os elementos do universo
que não pertencem ao conjunto A.
Notacão: A’ ou AC
Simbolicamente: A '  x / x  U  x  A
A’ = U - A
Exemplo:
U = {1; 2; 3; 4; 5; 6; 7; 8; 9} e A = {1; 3; 5; 7; 9}
U
A
2
6
3
1
5
8
7
A’ = {2; 4; 6; 8}
9
4
PROPRIEDADES DO COMPLEMENTO
1. (A’)’ = A
4. U’ = Φ
2. A U A’ = U
5. Φ’ = U
3. A  A’ = Φ
ÍNDICE
A
B
A
B
[(AB) – C]
A
C
B
B
A
C
C
[(AC) – B]
U
U
C
[(BC) – A]