A resolução de problemas

posição — Exercícios — Exposição — Exercícios — Exposi
Exposição
Resolução de exercícios
Trabalho prático, experimental
Exploração, investigação, resolução de problemas
Discussão
Na aula de Matemática
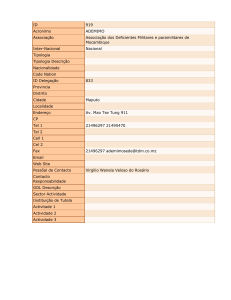
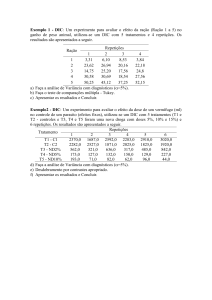
1
Respostas de alunos (2004-2005))
O que é um problema?
“Situação que requer resposta ou resolução não imediata”
“Uma questão em que existe algo a descobrir”
“Algo sobre que nos questionamos para encontrar uma solução”
“Um problema remete para a reflexão de modo a conseguir
contorná-lo”
“Questão que suscita dúvidas”
“Tarefa para despertar a curiosidade e o entusiasmo”
“Desafio” “Inquietação” “Obstáculo”
“Apelo à autosatisfação ”
”É problema enquanto não for encontrada resposta”
2
Respostas de alunos (2001-2002))
O que é um problema?
“Uma questão para a qual a resposta não é imediata”
“Uma questão em que existe algo a descobrir”
“Algo sobre que nos questionamos para encontrar uma solução”
“Coisa que [nos] move a pensar”
“Situação que suscita dúvidas”
“Situação que provoca curiosidade, desperta a atenção”
“Desafio”
“Enigma” “Incógnita”
“Situação [cujo] desenvolvimento implica uma atitude
empenhada”
“... Depende do conhecimento que cada pessoa possui”
3
Respostas de alunos (1999-2000)
O que é um problema?
“É uma questão ... cuja resolução não é evidente”
“É uma questão cuja solução não é óbvia”
“É uma situação que suscita dúvidas”
“É uma situação que pode gerar várias interpretações”
“É algo que põe em acção os nossos conhecimentos ...
na tentativa de encontrar a sua solução”
“É uma situação ... para a qual procuramos uma resposta
ou solução”
“É uma dificuldade com que nos deparamos”
“É um desafio”
4
O que é um problema?
Problema: s. m. questão que se propõe para ser resolvida;
coisa difícil de compreender, explicar ou fazer; dúvida. (Do
grego probléma, -atos, “questão proposta”.
[Dic. língua portuguesa, Costa & Melo, 1994, Porto: P. Editora]
Problema: dificuldade; dúvida; enigma; mistério; proposição;
quebra-cabeça; questão.
[Dic. de sinónimos, Tertúlia Edípica, 1990, Porto: P. Editora]
Problema: de proballetu, “lançar”, “atirar”, “propor”. Em
geral, tudo aquilo que se opõe ou resiste à penetração da
inteligência, constituindo uma incógnita ou dificuldade a
resolver.
[Enc. Luso-brasileira de cultura, M. Freitas, 1973, Lisboa:Verbo]
5
O que é um problema?
“Um indivíduo está perante um problema quando se
confronta com uma questão a que não pode dar resposta, ou
com uma situação que não sabe resolver, usando os
conhecimentos imediatamente disponíveis.”
[M. Kantowsky, 1977]
“Um problema é uma tarefa para a qual o indivíduo ou o
grupo que com ela se confronta quer ou precisa de encontrar
uma solução [e] não há procedimento prontamente acessível
que garanta ou determine, completamente, a solução.”
[F. Lester, 1983]
Tarefa, questão ou situação que nos
interessa realizar, responder ou resolver, e
não dispomos previamente de uma
estratégia para o fazer.
6
George Pólya
“No ensino da Matemática, podem
fazer-se necessários problemas
rotineiros, até mesmo muitos deles,
mas deixar que os alunos nada mais
façam é indesculpável”
7
G. Pólya
Compreensão do problema
Estabelecimento de um plano
Execução do plano
Análise retrospectiva
8
Um exemplo: a diagonal do paralelipípedo
x
x
a
a
c
b
x 2 = y 2 +a2
y 2 =c2 +b2
x 2 =a2 +b2 +c2
x
y
b
y
c
x = a2 +b2 +c2
9
Um exemplo: a diagonal do paralelipípedo
x
x
c
a
b
c
b
a
10
Um exemplo: a diagonal do paralelipípedo
x
a
x
c
b
c
x
a
c
b
a
b
c
x
b
x
b
c
a
11
Standards 2000
As Normas
Números e operações
Álgebra
Geometria
Medida
Análise de dados e probabilidades
Resolução de problemas
Raciocínio e demonstração
Comunicação
Conexões
Representação
12
Nos programas actuais
Papel no currículo:
• Uma das “finalidades”
• Um “eixo organizador”
• Um “contexto no qual se constroem con[ceitos e descobrem relações”
• Uma “actividade que estimula o espírito
[de pesquisa”
“Para a aquisição de conhecimentos deve partirse preferencialmente de situações problemáticas”
13
Influências na resolução de problemas
Factores que influenciam a
resolução de problemas
Meio ambiente
Aspectos ambientais:
- materiais, sociais…
Indivíduo
Problema
Aspectos matemáticos:
- conteúdo, estrutura…
Aspectos de formulação:
- contexto, linguagem…
Características constitucionais
Características de personalidade
Biografia escolar
…
14
A resolução de problemas no ensino
(perspectivas de utilização)
Motivação
(antes)
Aprendizagem
Aplicação
Aprendizagem
(depois)
Contexto
(durante)
Aprendizagem
15
A resolução de problemas no ensino
(perspectivas de utilização)
Do ponto de vista do professor:
Objectivo
Ensinar para (resolver problemas)
(Aplicação)
Conteúdo
Ensinar a (resolver problemas)
Método
Ensinar através de (resolver problemas)
(Contexto)
16
A resolução de problemas no ensino
(tarefas)
Exposição
Resolução de exercícios
Trabalho prático, experimental
Exploração, investigação, resolução de problemas
Discussão
Trabalho individual - Trabalho em pares - Trabalho em grupo - Trabalho colectivo
17
A resolução de problemas no ensino
(do ponto de vista do aluno)
Conhecimentos
Capacidades
Experiência matemática genuína
Visão mais ampla e completa da Matemática
Expectativas elevadas a aprendizagem
Atitudes
18
Porquê a resolução de problemas?
Razões metodológicas
Razões formativas
Razões epistemológicas
“A educação matemática não é mais do que o
desenvolvimento da actividade matemática e não
existe actividade matemática sem problemas.”
A. Krigowska (1970)
“Se a lógica é a higiene do matemático, ela não é
aquilo que o alimenta; são os grandes problemas
que fornecem o alimento quotidiano com o qual o
matemático se desenvolve.”
A. Weil , in J. Fang, 197019
O coração da Matemática
“De que é que a Matemática consiste verdadeiramente?
Axiomas...? Teoremas...? Demonstrações...
Definições...? Teorias...? Fórmulas...? Métodos…?
A Matemática certamente não existiria sem estes ingredientes. Todos eles são essenciais.
É todavia sustentável que nenhum desses ingredientes
está no coração da Matemática, que a principal razão
de existir de um matemático é resolver problemas e
que, por isso, aquilo de que verdadeiramente a
Matemática consiste, é de problemas e das suas
soluções.”
Paul Halmos The heart of mathematics (1980)
20