Lógica e Computação : Uma leitura dos Teoremas de Gödel

Lógica e Especificação
Módulo II: Sistemas Dedutivos
Edward Hermann Haeusler
Departamento de Informática
TECMF
PUC/RJ
Sistemas Dedutivos e Argumentação Formal
Def1. Um sistema dedutivo é um mecanismo que permite a construção
de argumentos formais
Def2. Um sistema dedutivo é um mecanismo que permite estabelecer
conclusões a partir de hipóteses.
Def3. Um sistema dedutivo é um conjunto de regras (as vezes axiomas)
que permite “chegar” a conclusões (sentenças) a partir de
hipóteses (sentenças).
Def4. Um sistema dedutivo é um conjunto de regras (as vezes axiomas)
onde os axiomas são fórmulas válidas e as regras preservam
a verdade.
Edward Hermann
Lógica e Especificação
2
Universalidade da noção de
correto
O conceito de argumento correto deve ser
baseado na forma do mesmo e não em seu
significado particular, ou
Um argumento é correto quando é invariante
sob substituição, i.e., o que importa é o relacionamento entre premissas e conclusão e
não estas propriamente ditas.
Edward Hermann
Lógica e Especificação
3
Os sistemas a la Frege/Hilbert
Esquemas de Axiomas:
(K)
A(B A)
(S)
A (B C)  (A B) (A C)
(Cla)  A A
Regra:
A
(Modus Ponens)
Edward Hermann
AB
B
Lógica e Especificação
4
Exemplos de Deduções
(K)
(K)
X(Y X)
X(Y X)
(S)
A ((A  A)  A)
X (Y Z)  (X Y) (X Z)
A ((A  A)  A) ( (A(AA))  (AA))
(A(AA))  (AA)
A(AA)
AA
Edward Hermann
Lógica e Especificação
5
Cálculo de Sequentes (Gentzen 1935)
Edward Hermann
Lógica e Especificação
6
Em uma mansão a polícia investiga um crime. Sabe-se que
mordomo, a cozinheira e a governanta são suspeitos. Se o
cozinheira é inocente então a governanta é culpada; ou a mordomo ou a governanta são culpadas, mas não ambos. O mordomo
não é inocente. Quem são os culpados ??
Proposições
C : Cozinheira Culpada
G : Governanta Culpada
M : Mordomo Culpado
Declarações sobre o crime:
1- Se o cozinheira é inocente então a governanta é culpada : C  G
2- Ou o mordomo ou a governanta são culpados : M  G
3 - mas não ambos :  (M  G)
4 - O mordomo não é inocente : M)
Edward Hermann
Lógica e Especificação
7
Discussão:
1- O método da “tabela verdade” é um sistema dedutivo ??
2- O que dizer do sistema dedutivo somente com a regra de
modus ponens e como axiomas todas as fórmulas válidas (tautologias)
3- Como comparar sistemas dedutivos ??
4- O que a prova de um teorema deve nos dizer ??
5- O que Prova de Teoremas tem a ver com computação e programação ?
Edward Hermann
Lógica e Especificação
8
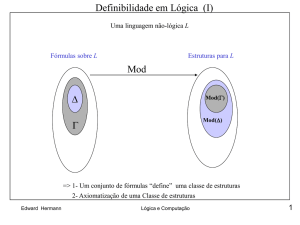
Consequência Dedutiva
Sejam Gum conjunto de fórmulas e a uma
fórmula.
G
a Existe uma dedução de aa partir de
G.
Cn(G) = { a / Ga}
Cn() =
Edward Hermann
Lógica e Especificação
9
O que se espera de um sistema dedutivo S ?
Correção :
Se G
S
aentão Ga.
Completude : Se Gaentão G
a.
S
Teorema : Cálculo de Sequentes é um sistema
dedutivo correto e completo em
relação à semântica clássica prop.
Edward Hermann
Lógica e Especificação
10
Definições e Fatos Importantes
- Seja S um sistema dedutivo completo e correto, então:
Def. Um conjunto de fórmulas  é inconsistente, sss, 

S
Fato I.  é inconsistente, sss,  é não é satisfatível (insatisfatível).
Fato II. 
a, sss,   {a} é insatisfatível.
S
Edward Hermann
Lógica e Especificação
11

O que se pode expressar na linguagem da
lógica proposicional ?
 Como expressar propriedades ?
Como qualificar objetos ?
Como generalizar conceitos ?
Edward Hermann
Lógica e Especificação
12
A Linguagem de primeira ordem
Todo
Homem
é
propriedade
objeto de
uma classe
ref.
Toda
Mortal

Conjunto
Predicado
||
Conjunto
Toda referência ao conjunto dos homens pertence
ao conjunto dos mortais.
Edward Hermann
Lógica e Especificação
13
Interpretação em aberto...
Todo elemento pertencente conjunto denotado por
Homem pertence ao conjunto denotado por Mortal.
"x ( H (x) M (x) )
referência
Edward Hermann
conjunto
Lógica e Especificação
conjunto
14
Funções e Relações
Opai de João é colega de Denise
João
pai
Pai(João)
Denise
colega
Pai(João)
colega(Denise, pai(João))
Edward Hermann
Lógica e Especificação
15
Formalizando
Símbolos lógicos
Alfabeto
"~}
+
variáveis
Símbolos não lógicos = definidos pelo
usuário
constantes
Edward Hermann
símbolos
funcionais
Lógica e Especificação
símbolos
predicativos
16
Interpretação e Semântica
Linguagem = < Lula, FHC, Irmão-de, Pai-de>
I associa os elementos da linguagem aos seus “significados”
I(FHC) =
I(Lula) =
I(Irmão-de) =
I(Pai-de) =
Ver(I, Irmão(Lula, FHC)) = V
Edward Hermann
Ver(I, x.Pai-de(Lula, x)) = V
Lógica e Especificação
17
Some Quantifers Proterties
Edward Hermann
Lógica e Especificação
18
Uma estrutura para interpretar um linguagem L
de primeira ordem é um objeto do tipo :
M = [ D, Pred, Func ]
 onde :
D é um conjunto
Para cada s. funcional f, de aridade n, de L
n
M associa uma função F : D D em Func.
Para cada s. predicativo p, de aridade n, de L
n
em Pred.
M associa uma relação P  D
Edward Hermann
Lógica e Especificação
19
Exemplo
Seja a linguagem L com :
- Constantes : 0
obs: Constantes podem ser vistas
como Funcionais de aridade 0
- Funcionais : s, +, * , E
- Predicativos : <
Uma possível estrutura é :
M = [N, <, 0, suc, +, *, E ]
com E sendo a função de expoenciação.
Edward Hermann
Lógica e Especificação
20
Outros exemplos
1- L=<, >
O que pode-se expressar nesta linguagem ?
Quem pode ser estrutura para esta linguagem ?
2a- L=< {v0},{2}>
2b- L=<{2,i0}, >
O que pode-se expressar nesta linguagem ?
Quem pode ser estrutura para esta linguagem ?
3- L=<  , {E2,D2,V0}>
O que pode-se expressar nesta linguagem ?
Quem pode ser estrutura para esta linguagem ?
Edward Hermann
Lógica e Especificação
21
Como atribuir valor verdade às fórmulas ?
 P(t1, ..., tn) é verdadeira em uma estrutura
M sse, a interpretação da n-upla <t1, ..., tn>
pertence a relação que denota P, em M.
Como interpretar variáveis ?
Associa-se a cada variável um elemento do
domínio, via uma funcão n.
Assim :
 P(t1, ..., tn) é verdadeira em uma estrutura
M sob uma função nsse, a interpretação da
n-upla <t1, ..., tn> pertence a relação que
P(t1, ..., tn))
denota P, em M. (< M,n>
Edward Hermann
Lógica e Especificação
22
Fórmulas existênciais e universais
n(y) se y  x
n[a/x](y) =
a se y = x
< M,n >
"xa, sse para todo a Dom( M )
< M, n[a/x] >
a.
< M,n >
xa, sse existe a Dom( M )
< M, n[a/x] >
a.
Edward Hermann
Lógica e Especificação
23
Exemplos de fórmulas verdadeiras em
[N, <, 0, s, +, *, E ]
Sendo :
Div(x,y) x  0 )  k( k*x = y)
Par(x) Div(s(s(0)),x)
Primo(x) x  s(0)) "y( Div(y,x) y = s(0) y = x)
 n (Primo(n) Par(n))
Edward Hermann
Lógica e Especificação
24
Outra estrutura para a mesma linguagem
S = [Q, <, 0, suc, +, *, E ]
com :
Q Racionais,
< é a ordem usual,
s (m/n) = m/n + 1,
k
E( m/n , k/j )= m
+ e * usuais.
S
"x"yk(x  k y  k x < k k < y)
Obs : Omitimos a função nquando a relação semântica se dá para todas
as funções.
Edward Hermann
Lógica e Especificação
25
Exemplo em LPO
3
Linguagem escolhida:
G(t,x,y) = “no instante t a garrafa de 5L tem x litros e
a de 7L tem y”
s(t) = “o próximo instante de tempo depois de t”
Edward Hermann
Lógica e Especificação
26
Fórmulas que especificam as restrições do problemas
Edward Hermann
Lógica e Especificação
27
Prova de que é possível medir 3 litros
Edward Hermann
Lógica e Especificação
28
 Entendendo o par <M, n> como uma interpretação :
Dedução Natural clássica é correta e
completa para a linguagem de primeira
ordem.
[Compacidade].
- Ga, sse para algum Gfinito, a.
- Gé satisfatível, sse, todo G finito
é satisfatível.
Edward Hermann
Lógica e Especificação
29
Mundo Linguistico
M
Mundo "real"
Th(M)
Cn
Cn
Cn
Cn
M
Edward Hermann
Lógica e Especificação
30
Bibliografia
1- Teoria das Categorias e Ciência da Computação.
Menezes, P.B. & Haeusler, E.H. Editora Sagra-Luzzato(Caps. 2 e 7)
2- Logic and Structure. Dirk van Dalen. Springer-Verlag. (3rd edição)
3- A Mathematical Introduction to Logic. H.B. Enderton.
4- Logics of Time and Computation. Robert Goldblatt. CSLI
5- Epistemic Logic for AI and Computer Science. Meyer & Van der Hoek
(Cambridge Tracts in Computer Science). (Caps 1 a 3)
6- Computational Complexity (Cap. 5)
7- Handbook of Description Logic. (Cap. 1 e 2).
Edward Hermann
Lógica e Especificação
31