No Slide Title

Lógica de Primeira Ordem
1- Modelos e Teorias
2- Definibilidade de (classes de) Estruturas (s)
3- Definibilidade em um estrutura
Ref ==> Seções 2.1 e 2.2 de [Enderton]
Edward Hermann
Lógica e Especificação
1
Modelos e Teorias
Algumas Definições Úteis
Sejam - L uma linguagem não-lógica de primeira ordem,
- Est(L) a classe de todas as estruturas para L
- Sent(L) o conjunto das sentenças de L
Def. Seja   Sent(L). Define-se Mod() = { S / S  Est(L) e S |= 
}
Def. Sejam C  Est(L) e   Sent(L). Diz-se que a classe de estruturas C satisfaz
 (C |=  , em símbolos) , sss, para toda estrutura S  C tem-se S |= 
Def. Seja C  Est(L). Define-se Th(C) = {  /   Sent(L) e C |=  }
Def. Seja D um sistema dedutivo correto e completo para a LPO. Nota-se  |-  ,
sempre exista uma prova de  a partir de  em D.
Def. Cn() = { /  |-  }
Edward Hermann
Lógica e Especificação
2
Modelos e Teorias
Uma linguagem não-lógica L
Fórmulas sobre L
Estruturas para L
Th
C
Th(D)
D
Th(C)
=> 1- O que Th({S}) tem de especial ???
2- Th({S}) como uma descrição lingüística de S.
Edward Hermann
Lógica e Especificação
3
Modelos e Teorias
Definição Importante em Lógica e Ciências Formais
Seja L uma linguagem da LPO.
Def.   Formulas(L) é uma teoria, sss, para toda   Formulas(L) , tem-se:
  T , se e somente se, T |- 
Fato: T  Formulas(L) é uma teoria , sss, Cn(T) = T.
Def. T  Formulas(L) é completa sss, para toda   Formulas(L) , tem-se que
ou   T ou   T.
Edward Hermann
Lógica e Especificação
4
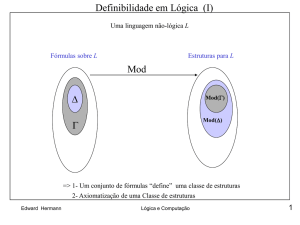
Definibilidade em Lógica (I)
Uma linguagem não-lógica L
Sentenças sobre L
Estruturas para L
Mod

Mod()
Mod()

=> 1- Um conjunto de fórmulas “especifica” uma classe de estruturas
2- Axiomatização de uma Classe de estruturas
Edward Hermann
Lógica e Especificação
5
Modelos e Teorias
Exercícios:
Verifique se é falso ou verdadeiro:
1- Cn(1  2) = Cn(1)  Cn(2)
2- Cn() = Th(Mod())
3- Se 1  2 então Cn(2)  Cn(1)
4- Se C1  C2 então Th(C2)  Th(C1)
5 -   Th(Mod()) e
C  Mod(Th(C))
6 - Mod()  Mod(Th(Mod())) e Th(C)  Th(Mod(Th(C)))
7- Th(C1)  Th(C2) = Th(C1  C2)
Edward Hermann
Lógica e Especificação
6
Questões Naturais :
1- Todo conjunto de fórmulas (sobre L) define uma classe de estruturas ??
2 - Qual o conjunto de fórmulas que define a classe de todas as estruturas
para uma linguagem L ?
3- Toda classe de estruturas é definível por um conjunto de fórmulas, ou
seja todas as classes de estruturas são elementares ??
4- Toda classe de estruturas é definível por uma única fórmula ??
=> Existem classes não elementares
Edward Hermann
Lógica e Especificação
7
Teorema da Completude:  |= 
se e somente se  |- 
Teorema da Compacidade:  é finitamente satisfatível sss  é satisfatível
Teorema da Compacidade:  é finitamente satisfatível sss  é satisfatível
 finitamente satisfatível = Para todo  finito com    tem-se  sat.
=> A Classe das estruturas (para L fixa) infinitas não é definível por nenhuma
fórmula. (isto é, não é elementar)
=> A Classe das estruturas (para L fixa) finitas não é definível por nenhum
conjunto de fórmulas
Edward Hermann
Lógica e Especificação
8
Definibilidade em Lógica (I)
Para cada estrutura S tem-se a linguagem LS da estrutura
Estrutura S
Fórmulas para LS
Th
Cn
 Cn
Th(S)
1- Definibilidade de uma (classe de) estrutura (s) !!!!
2- Axiomatização da Teoria de uma Estrutura
Edward Hermann
Lógica e Especificação
9
Definibilidade em Lógica (II)
Definibilidade em uma estrutura:
(x1,...,xn) uma fórmula na linguagem da estrutura S
(x1,...,xn) define uma relação n-ária (um subconjunto de Sn)
[[(x1,...,xn) ]] = { <a1,...,an> / ai |S| e |=
(x1,...,xn) }
<S,[a1/x1,...an/xn]>
Exemplos:
1. Em <N,suc>: [[y(suc(y)=x)]]={0}, [[z (y(suc(y)=z)(suc(z)=x)]]={1} e
[[suc(suc(x1)=x2)]]={<a1,a2>/ a1+2=a2 e a1,a2  N}
2. Em <R,,+>: [[y(+(y,x)=y]]={0}, [[y((y, y)=x)]]={r / r  R e r0},
[[y((x1+y=x2)  (+(y,y) y))]]={<r1,r2> / r1<r2 e r1,r2  R
Obs: Às vezes a notação infixa é usada : x+y no lugar de +(x,y)
Edward Hermann
Lógica e Especificação
10
Definibilidade em Lógica (I)
Homomorfismo de Estruturas
h
P
PQh
s
h(s)
b
h(b)
a
h(a)
h(f(a,b)) = fh(h(a),h(b))
f(a,b)
= g(h(a),h(b))
S1
<|S1|,f,P>
|S1|
h
f
P
Edward Hermann
Lógica e Especificação
|S2|
S2
g
fh
Q
Ph
<|S2|,g,Q>
11
Definibilidade em Lógica (I)
Subestruturas e Extensões
Def. Sejam S1 e S2 duas estruturas tais que a função de inclusão S1 S2
é um homomorfismo. Diz-se que S1 é subestrutura de S2, e que
S2 é uma extensão de S1.
Def. Sejam S1 e S2 duas estruturas e h: S1 S2 um homomorfimo
bijetivo (injetivo e sobrejetivo), então h é dito ser um isomorfimo
de estruturas e S1 é dita ser isomorfa a S2 (S1 S2)
=> Estruturas isomorfas satisfazem as mesmas fórmulas ???
=> Estruturas que satisfazem as mesmas fórmulas são isomorfas ???
Edward Hermann
Lógica e Especificação
12
Definibilidade em Lógica (I)
Teorema do homomorfimo: Seja
|= P(t1,...,tn)
sss
<S1,>
h homomorfismo de S1 em S2 (estruturas para L)
Vars
|= P(t1,...,tn)
<S2,h>

h
|S1|
h
|S2|
<(t1),....., (tn)>  PS1
sss
<h((t1)),....., h((tn))>  PS2
a
h(a)=h(b)
1. Se  não possui quantificadores nem a igualdade.
b
2. Se  não possui quantificadores mas sim a igualdade e
h é um homomorfismo injetivo
S1
S2
3. Se  possui quantificadores e mas não a igualdade e
h é um homomorfismo sobrejetivo
h(|S1|)
t1=t2
|= 
<S1,>
x
Edward Hermann
sss
|= 
t1=t2
<S2,h>
c
x
Lógica e Especificação
S1
S2
13
Definibilidade em Lógica (II)
Homomorfismo e Definibilidade
Def. Um Automorfismo é um isomorfismo (homomorfismo bijetivo) de uma estrutura
nela mesma.
Corolário: Seja S uma estrutura e h:S
S um automorfismo, então ASn é definível,
se e somente se, h(A) Sn é definível.
==> O Corolário acima é uma boa ferramenta para mostrar que algumas relações/conjuntos
não são definíveis.
Exemplos:
1- Na estrutura <N> nenhum conjunto diferente do vazio e do N é definível (em particular o
número zero não é definível). Qualquer função bijetiva é um automorfismo em N.
2- Em <N,> a adição não é definível, pois o a função:f(0)=0,f(1)=1 f(3)=2, f(2)=3 e
f(p1  p2)=f(p1)  f(p2) se caso contrário, é um automorfismo em <N ,> que não
preserva a adição.
Edward Hermann
Lógica e Especificação
14
Definibilidade em Lógica (II)
Relações de extensibilidade própria entre estruturas sobre N.
<N, ,+ >
<N,  >
<N,+>
< N,< >
<N,s>
Edward Hermann
Lógica e Especificação
15