Ambientes de Mercado

Universidade Federal de Itajubá
Instituto de Engenharia de Produção e Gestão
Determinação de Preços
mercados perfeitos, monopólios e oligopólios
Prof. Dr. Fred Leite Siqueira Campos
Desenvolvimento da Aula
1.Concorrência Pura:
Características de mercados puros;
Curvas de demanda de mercado;
Curvas de demanda individual;
Comportamento da firma;
2.Monopólio:
Características do monopólio;
Demanda da firma monopolista;
Estabelecimento de preços com Mark-up;
Comportamento da firma monopolista;
3.Oligopólio:
Características de mercados oligopolistas;
Modelo de Cournot;
Modelo de Stackelberg;
Modelo de Bertand;
Ambientes de Mercado
•
Toda empresa se depara com duas decisões:
1. escolha do volume de produção;
2. escolha do preço de seu produto;
•
Toda empresa enfrenta dois tipos de restrições:
•
Restrições tecnológicas (função de produção);
•
Restrições de mercado (uma empresa pode produzir
qualquer coisa que se deseja fisicamente factível e
pode fixar qualquer preço que deseje, mas só poderá
vender se as pessoas quiserem comprar).
Concorrência Pura
•
Compradores e vendedores são price takers;
•
Mercado atomizado;
•
Produto homogêneo;
•
Informação perfeita;
•
Livre mobilidade;
•
Não há lucros no LP;
•
Modelo teórico e estilizado.
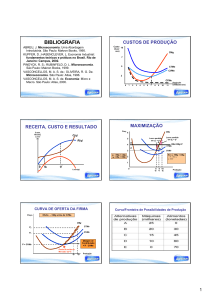
Curvas de Demanda de Mercado
p
s
• O preço é determinado pelas
forças de mercado da oferta e da demanda;
p*
D
Q
Curvas de Demanda Individual
Preço é dado, por isso curva de demanda percebida por uma firma
individual deve ser infinitamente elástica, indicando que o preço p* que
essa firma pode cobrar pelo seu produto é igual ao preço de mercado,
independetemente de quanto essa firma produz.
p
d
p*
A firma toma esse preço como um dado
que ela não pode afetar, assim, sua
curva de demanda é uma linha
horizontal com altura igual ao preço de
mercado.
Q
Comportamento da firma
• firma busca maximizar o lucro (lucro = receita – custo)
RT  p.q
RT p.q
RMe 

p
q
q
RT p.q
RMg 

p
q
q
p
p = d = RMg = RMe
q
Comportamento da firma
 (q)  RT (q)  CT (q)
Condição de máximo de primeira ordem para essa função:
 (q)
RT (q) CT (q)
0

0
q
q
q
RMg  CMg  0
RMg  CMg
Monopólio
•
Vendedores não são price takers;
•
Mercado não atomizado;
•
Produto heterogêneo;
•
Informação perfeita;
•
Exitência de lucro no LP;
•
Barreiras.
Demanda da firma Monopolista
• A curva de demanda individual de uma firma monopolista é negativamente
inclinada (coincidente com a curva de demanda de mercado);
• RMg < p
• Preço de venda da mercadoria do monopolista é dado pela demanda do
mesmo, isto é, ele depende da quantidade (q) colocada à venda (p=p(q) e como
p diminui q aumenta).
RT  q. p(q)
RT q. p(q)
p
RMg 

 pq
q
q
q
p
 0  RMg  p
q
Demanda da firma Monopolista
• Supondo curva de receita marginal quando a demanda é linear.
p  a  bq
2
RT  aq  bq
RMg  a  2bq
p
RMg é duas vezes mais inclinada que a curva
de demanda.
d = RMe
RMg
p=a-bq
q
Estabelecimento de preços com
Mark-up
RT  q. p(q)
RT q. p(q)
p
RMg 

 pq
q
q
q
q p

p q
Elasticidade-preço da demanda
p
RMg  p  q
 p
q
 q p 

p
 p q 




1

RMg  p  1 
p q 


q p 

  1 RMg  0
  1 RMg  0


1
 1
p1    RMg  p1  
 
  
Comportamento da firma
 (q)  RT (q)  CT (q)
Condição de máximo de primeira ordem para essa função:
 (q)
RT (q) CT (q)
0

0
q
q
q
RMg  CMg  0
RMg  CMg
Estabelecimento de preços com
Mark-up
O lucro máximo é obtido quando o CMg = RMg.
CMg

1 

RMg  p1  
  
CMg


1
CMg  p1  
  
p’
p  CMg
d
q
q
RMg
RMg  CMg
Mark-up
1


1
1  





Oligopólio
•
Poucos vendedores;
•
Produtos podem ou não ser diferenciados;
•
Ações de cada vendedor afetam todos os outros vendedores;
•
Formas de oligopólio:
•
Oligopólio com produto homogêneo;
•
Oligopólio com diferenciação de produto;
•
Modelo em que as firmas competem entre si, alterando a
quantidade produzida (Modelo de Cournot, Modelo de
Stackelberg );
•
Modelo em que as firmas competem entre si, alterando o preço
do produto (Modelo de Bertrand).
Modelo de Cournot
Esse modelo pressupõe que cada uma das firmas que compõem o oligopólio
toma a quantidade produzida pelas outras firmas como um dado que ela não
pode alterar (fixo).
RT1  p(q1  q2 )q1
RT2  p(q1  q2 )q2
RT1
 pq1  q2  p' (q1  q2 ) q1
q1
RT2
RMg 2 
 pq1  q2  p' (q1  q2 ) q2
q2
RMg 1 
CMg1 (q1 )  pq1  q2   p' q1  q2 q1
CMg2 (q2 )  pq1  q2   p' q1  q2 q2
Modelo de Cournot
p  a  b(q1  q2 )
1e  pq1  aq1  bq12  bq1q2
 1e
e
q1
a/b
 a  2bq1  bq2  0
a  bq2e
q1 
2b
a
q1  q2 
3b
2a a
p  a b

3b 3
q2
Curva de reação
da firma 1
a / 2b
a / 3b
Curva de reação
da firma 2
a / 3b a / 2b
a  bq1e
q2 
2b
a/b
q1
Um exemplo: Cournot
Duas empresas idênticas se defrontam com uma curva de demanda linear de
mercado e que custo marginal de ambas é igual a zero:
P  30  Q Q  q1  q2
CMg1  CMg2  0
Curva de Reação de 1:
RT1  pq1  (30  Q)q1
RT1  30q1  (q1  q2 )q1
RT1  30q1  q12  q1q2
RMg 
R1
 30  2q1  q2
q1
CMg1  RMg1
30  2q1  q2  0
1
q1  15  q2
2
Curva de Reação de 1
Curva de Reação de 1
Curva de Reação de 2
1
q1  15  q2
2
1
q2  15  q1
2
q1
30
Curva de
Reação de 2
Equilíbrio Competitivo
15
Equilíbrio Cournot
Equilíbrio Coalizão
10
7,5
Curva de
Reação de 1
7,5 10
15
30
q2
Modelo de Stackelberg
Esse modelo pressupõe que apenas uma das firmas reconhece que, à medida
que modifica sua quantidade produzida, ela induz uma modificação na quantidade
produzida por sua concorrente. A outra firma continua a comportar-se como em
Cournot. (Supondo que a firma 1 seja a líder)
max p1 (q1  q2 )q1  CT1 (q1 )
max  1  aq1  bq  bq1q2
2
1
q2  g (q1 )
Sujeito a
a  bq1
q2 
2b
Resolvendo por Lagrange
a
q1 
2b
a
q2 
4b
3a
Q  q1  q2 
4b
3a a
p  a b

4b 4
Função de
reação de 2
Um exemplo: Stackelberg
Duas empresas idênticas se defrontam com uma curva de demanda linear de
mercado e que custo marginal de ambas é igual a zero, empresa 1 é lider.
P  30  Q Q  q1  q2
CMg1  CMg2  0
Curva de Reação de 2:
RT2  pq2  (30  Q)q2
RT2  30q2  (q1  q2 )q2
RT2  30q2  q22  q1q2
RMg 
R2
 30  2q2  q1
q2
CMg1  RMg1
30  2q2  q1  0
1
q2  15  q1
2
Curva de Reação de 2
O que ocorre com a empresa 1?
RT1  pq1  (30  Q)q1
RT1  30q1  (q1  q2 )q1
1 

RT1  30q1  q  q1 15  q1 
2 

1
RT1  15q1  q12
2
2
1
R1
RMg 1 
 15  q1
q1
RMg1  0q1  15
A empresa 1 produz o dobro do que
produz a empresa 2 e gera um lucro duas
vezes maior. A empresa 1 foi beneficiada
por ter sido a primeira a escolher sua
produção.
1
q2  15  q1
2
q2  7,5
Modelo de Bertrand
As firmas fixam os preços de seus produtos e deixam que a demanda determine a
quantidade a ser produzida. O modelo supõe que o produto é homogêneo e cada
firma parte do princípio que o preço cobrado não deve alterar-se.
P  30  Q Q  q1  q2
CMg1  CMg2  3
suposições
A empresa com menor preço abastecerá o mercado, portanto, o equilíbrio será de
concorrência perfeita:
p1  p2  CMg1  CMg2  3