Aula 21 - Economia Para Engenharia De Produção

TP043 – Microeconomia –23/11/2009 – AULA 21
Bibliografia: PINDYCK capítulo 12 – Competição monopolística e oligopólio.
Características da competição monopolística:
1. Muitas empresas
2. Livre entrada e saída
3. Produtos diferenciados mas altamente substituíveis
Muitas empresas tentam conseguir poder de mercado criando marcas para fidelizar
o cliente e adquirir poder de monopólio. O tamanho do poder de monopólio depende do
grau de diferenciação do produto.
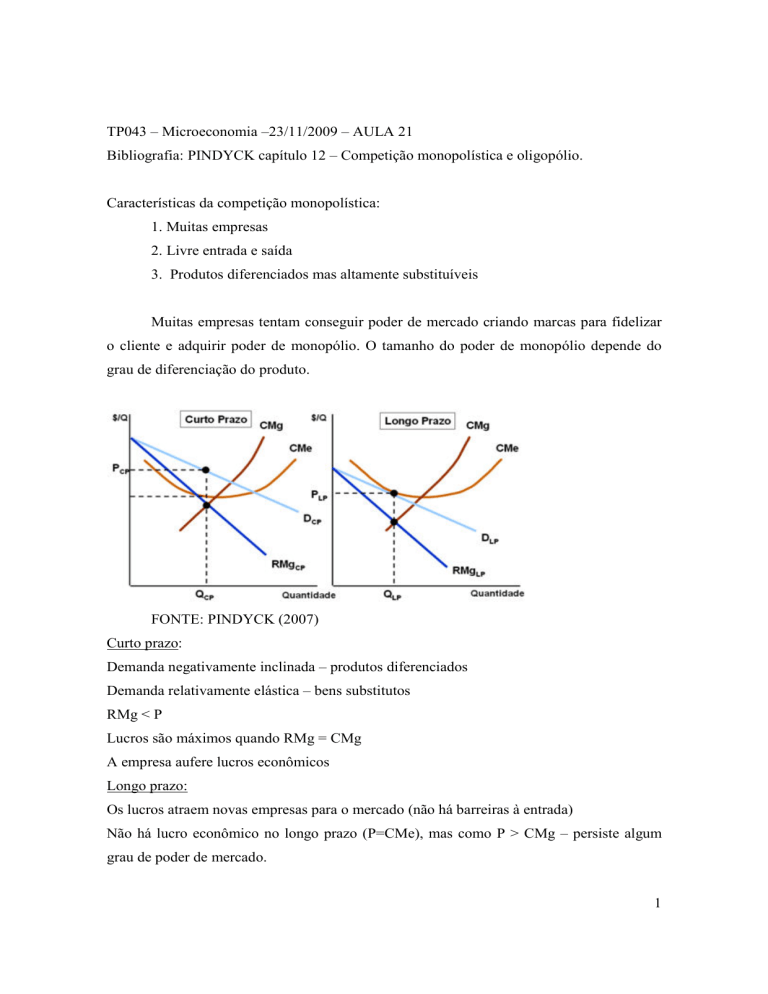
FONTE: PINDYCK (2007)
Curto prazo:
Demanda negativamente inclinada – produtos diferenciados
Demanda relativamente elástica – bens substitutos
RMg < P
Lucros são máximos quando RMg = CMg
A empresa aufere lucros econômicos
Longo prazo:
Os lucros atraem novas empresas para o mercado (não há barreiras à entrada)
Não há lucro econômico no longo prazo (P=CMe), mas como P > CMg – persiste algum
grau de poder de mercado.
1
Comparação do equilíbrio em competição monopolística e do equilíbrio em competição
perfeita:
FONTE: PINDYCK (2007)
Apesar de não haver lucro econômico no longo prazo, a empresa não produz no ponto de
CMe mínimo, e há excesso de capacidade.
Exemplos: Café e Refrigerantes cola:
Refrigerantes
Elasticidades
Royal Crown
-2,4
Coca-Cola
-5,2 a –5,7
FONTE: PINDYCK (2007)
A que tem maior poder de Mercado é a Royal Crown, pois é menos elástica. A
coca-cola, entretanto produz um lucro maior. Isso ocorre porque ela também vende
quantidades maiores.
OLIGOPÓLIO:
Características:
Pequeno número de empresas
Produtos diferenciados ou homogêneos
Barreiras à entrada
Exemplos: Automóveis, Aço, Alumínio, Petroquímicos, Equipamentos elétricos.
As barreiras à entrada em um mercado podem derivar de:
Economias de escala, patentes, acesso à tecnologia, reputação da marca, ação
estratégica, ameaça de inundação do mercado com produtos para que o preço caia, controle
de insumos essenciais.
2
Equilíbrio no mercado oligopolista
Nas outras estruturas de mercado estudadas, os produtores não levavam em
consideração a reação das empresas rivais ao tomarem suas decisões de produção e preços.
Já no oligopólio, os produtores devem levar em consideração a reação dos concorrentes na
determinação de sua produção e preços. O equilíbrio é atingido no sentido de que as
empresas estão fazendo o melhor que podem e não têm incentivos para mudar suas decisões
de produção e preços
Modelo de Cournot
É uma estrutura de duopólio, onde duas empresas competem entre si com um
produto homogêneo. Cada empresa considera fixo o nível de produção da rival ao tomar
sua própria decisão de produção.
FONTE: PINDYCK (2007)
Curva de reação:
A produção ótima de uma empresa é uma função decrescente do nível de produção
esperado da outra empresa.
FONTE: PINDYCK (2007)
3
Exemplo de equilíbrio de Cournot:
Duopólio
Demanda de mercado é P = 30 - Q
Onde: Q = Q1 + Q2
CMg1 = CMg2 = 0
Curva de reação da Empresa 1:
Receita Total, R1 = PQ1 = (30 − Q)Q1 =>é o preço multiplicado pela quantidade!
= 30Q1 − (Q1 + Q2 )Q1
= 30Q1 − Q12 − Q2Q1
Supondo que o custo marginal é igual a zero!
RMg1 = ∆R1 ∆Q1 = 30 − 2Q1 − Q2
RMg1 = 0 = CMg1
Curva de reação da Empresa 1
Q1 = 15 − 1 2 Q2
Curva de reação da Empresa 2
Q2 = 15 − 1 2 Q1
Equilíbrio de Cournot : Q1 = Q2
Q1 = 15 − 1 2(15 − 1 2Q1 ) = Q1 = 10 = Q2
Q = Q1 + Q2 = 20
P = 30 − Q = 10
FONTE: PINDYCK (2007)
Maximização do Lucro:
R = PQ = (30 − Q)Q = 30Q − Q 2
RMg = ∆R ∆Q = 30 − 2Q
RMg = 0 quando Q = 15 e RMg = CMg
4
Curva de coalizão:
Q1 + Q2 = 15
Mostra todas as combinações de Q1 e Q2 que maximizam os lucros totais
Q1 = Q2 = 7,5
O nível de produção é menor e os lucros são maiores relativamente ao
equilíbrio de Cournot.
FONTE: PINDYCK (2007)
O modelo de Stackelberg
Uma empresa determina seu nível de produção antes da outra. Por exemplo
uma empresa que consegue lançar um produto antes dos concorrentes.
CMg = 0
Demanda de mercado é P = 30 – Q, onde Q = produção total
A Empresa 1 toma a decisão de produzir primeiro; em seguida, a Empresa 2
toma sua decisão de produção
A Empresa 2 toma a produção da Empresa 1 como dada e, portanto,
determina sua produção a partir da curva de reação de Cournot : Q2 = 15 - 1/2Q1
Empresa 1
Escolhe Q1 de modo que:
RMg = CMg, CMg = 0 logo RMg = 0
R1 = PQ1 = 30Q1 - Q12 - Q2Q1
Substituindo Q2 pela curva de reação da Empresa 2:
R1 = 30Q1 − Q12 − Q1 (15 − 1 2Q1 )
= 15Q1 − 1 2 Q12
5
RMg1 = ∆R1 ∆Q1 = 15 − Q1
RMg = 0 : Q1 = 15 e Q2 = 7,5
Conclusão
A produção e o lucro da Empresa 1 é o dobro da produção da Empresa 2.
MODELO DE BERTRAND:
Baseada em decisões relativas a preços ao invés de quantidades. É um setor
oligopolístico com produtos homogêneos.
Hipóteses:
Produto homogêneo.
Demanda de mercado é P = 30 – Q, onde Q = Q1 + Q2
CMg = $3 para ambas as empresas e CMg1 = CMg2 = $3
No equilíbrio de Cournot, tínhamos:
P = $12
Q1 = Q2 = 9
π para ambas as empresas = $81
Suponha, agora, que as empresas concorram por meio de preços, em
vez de quantidades.
Equilíbrio de Nash:
P = CMg; P1 = P2 = $3
Q = 27; Q1 & Q2 = 13.5
π =0
Se uma aumentar o preço, perderá todo o mercado. Se outra reduzir o
preço, terá prejuízo, pois o preço ficaria abaixo do CMg.
Críticas ao modelo de BERTRAND:
No caso de produtos homogêneos, é mais razoável supor que as
empresas concorram por quantidades do que por preços.
Mesmo admitindo que as empresas concorram por meio de preços e
que escolham preços idênticos, o modelo não permite identificar a proporção
das vendas totais obtida por cada empresa. Nada garante que as parcelas de
mercado sejam iguais.
6
Concorrência de preços com produtos diferenciados
Quando os produtos são diferenciados, as parcelas de mercado de
cada empresa dependem não apenas dos preços de seus produtos, mas
também de diferenças no seu desempenho, durabilidade e design.
Hipóteses
Duopólio
Custo Fixo = $20
Custo Variável = $0
Demanda da Empresa 1: Q1 = 12 - 2P1 + P2
Demanda da Empresa 2: Q2 = 12 - 2P2 + P1
Onde P1 e P2 são os preços praticados pelas empresas 1 e 2,
repectivamente e Q1 e Q2 são as quantidades resultantes vendidas por elas.
Escolha de Preços:
Empresa 1 : π 1 = P1Q1 − $20
= P1 (12 − 2 P1 + P2 ) − 20
= 12 P1 - 2 P12 + P1 P2 − 20
Empresa 1: Se P2 é fixo:
Preço maximizador de lucro da Empresa 1 =
∆π 1 ∆P1 = 12 − 4 P1 + P2 = 0
Curva de reação da Empresa 1 =
P1 = 3 + 1 4 P2
Curva de reação da Empresa 2 =
P2 = 3 + 1 4 P1
Concorrência versus acordo: o dilema dos prisioneiros
Por que as empresas não determinam o preço de coalizão de forma
independente, com ambas produzindo as quantidades que elevam mais os
lucros? auferindo os lucros mais elevados associados ao acordo explícito?
CF = $20 and CV = $0
Demanda da Empresa 1 : Q = 12 − 2 P1 + P2
Demanda da Empresa 2 : Q = 12 − 2 P2 + P1
Equilíbrio de Nash : P = $4 π = $12
Coalizão :
P = $6 π = $16
7
Resultados possíveis
Se ambas cobram $6, π = $16
Se P1 = $6 e P2 = $4
então π 2 = P2Q2 − 20
= (4)[12 − (2)(4) + 6] − 20 = $20
π 1 = P1Q1 − 20
= (6)[12 − (2)(6) + 4] − 20 = $4
Matriz de Pay-off:
FONTE: PINDYCK (2007)
Dilema do prisioneiro.
Dois prisioneiros foram acusados de terem colaborado na prática de um crime e
estão em celas separadas, não podendo se comunicar. Para cada um deles, separadamente,
foi pedido que confessasse o crime. A pena dos prisioneiros encontra-se na matriz abaixo:
FONTE: PINDYCK (2007)
Resultados:
Caso combinassem preços, obteriam lucros maiores, portanto as empresas podem
praticar acordos explícitos ou implícitos. Entretanto, cada uma tem um forte incentivo a
‘furar’ o acordo, cobrando um preço mais baixo que lhe conferirá lucros mais elevados.
8