Lista de Exercícios sobre relações métricas na circunferência

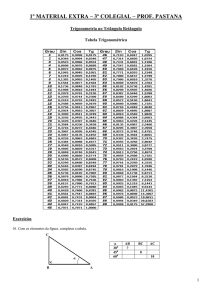
Versão 25/02/2016
Atividade complementar
Relações métricas na circinferência
Disciplina: Matemática
3ª Etapa
_____/_____/2016
Ano/Série: 8
Turma:
Educando:
Educador: Helder Tadeu
Ribeiro
Valor:
Nota:
1)
2)
3)
4)
5)
6)
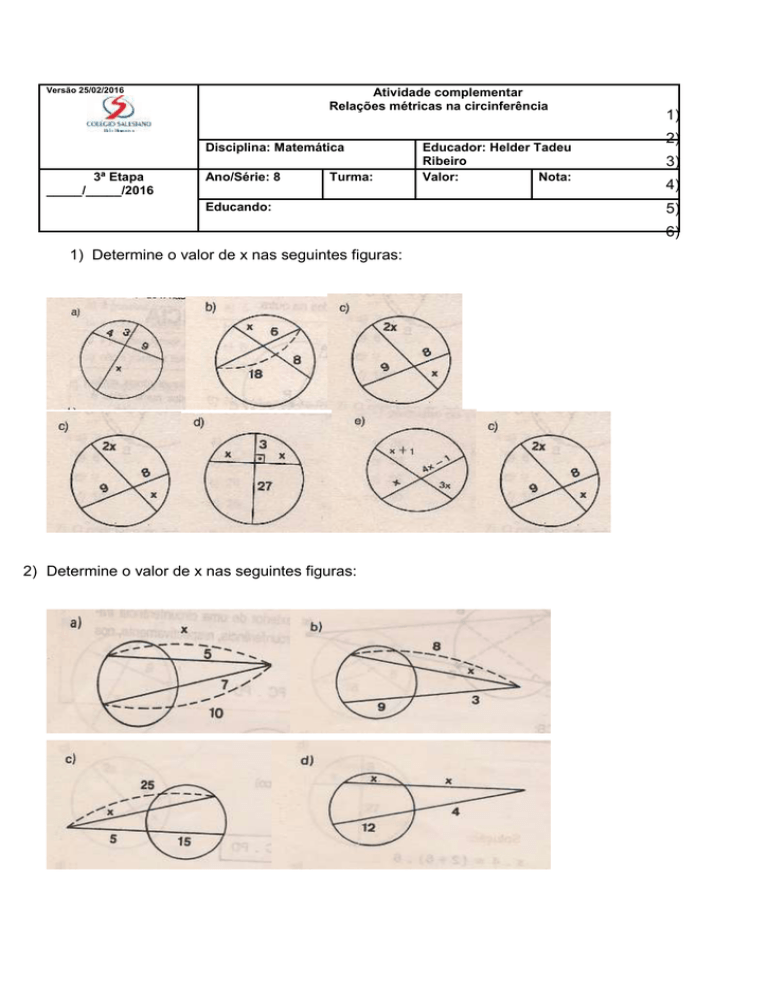
1) Determine o valor de x nas seguintes figuras:
2) Determine o valor de x nas seguintes figuras:
3) Determine o valor de x nas seguintes figuras:
4) Dada a figura abaixo, determine o valor de x e y:
5) Na figura, determine as medidas das cordas BD e CE , sabendo que:
AB = 3x, AC = 4x – 1, AD = x + 1 e AE = x.
6) Na figura abaixo, determine as medidas x e y indicadas.
7) Na figura abaixo, determine o comprimento r do raio, sabendo que PA = 8 cm e PC = 12
cm.
8) Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o solo. O
comprimento do fio é 80 m. determine a altura da pipa em relação ao solo. Dado 2 = 1,41
9) Qual é o comprimento da sombra de uma árvore de 5 m de altura quando o sol está 30º
acima do horizonte? Dado 3 = 1,73
10) Um observador vê um edifício, construído em terreno plano, sob um ângulo de 60º. Se ele
se afastar do edifício mais 30 m, passará a vê – lo sob ângulo de 45º. Calcule a altura do
edifício.
11) Determine a altura do prédio da figura seguinte:
12) Para determinar a altura de um edifício, um observador coloca – se a 30 m de distância e
assim o observa segundo um ângulo de 30º, conforme mostra a figura. Calcule a altura do
edifício medida a partir do solo horizontal. Dado 3 = 1,73
13) Observe a figura e determine:
a) Qual é o comprimento da rampa?
b) Qual é a distância do inicio da rampa ao barranco?
14) Determine qual era a altura do pinheiro da figura, considerando
3 = 1,73.
15) Qual é a largura do rio representado pela figura abaixo?
(Use: sen 53º = 0,80; cos 53º = 0,60; tg 53º = 1,32.)
16) Um navio, navegando em linha reta, vai de um ponto B até um ponto A. Quando o navio
está no ponto B, é possível observar um farol situado num ponto C de tal forma que o
ângulo ACB = 60º. Sabendo que o ângulo CAB é reto e que a distância entre os pontos A
e B é de 9 milhas, calcule a distância, em milhas:(Faça: 3 = 1,73)
a) do ponto A ao farol;
b) do ponto B ao farol.