(f)(x) + 1, se f(x)ul 0, caso contrário (f)(x) + 1, se f(x)wl - mtc

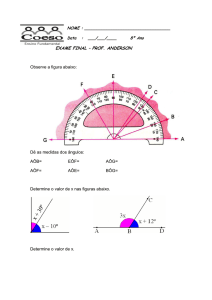
Instituto Nacional de Pesquisas Espaciais – INPE
Def. 3.2 – E
a
ŨZ
2
e
0
16
v l v n.
d l, e l, d l podem ser definidos de forma equivalente por:
ȡ
ȥ
+ Ȣ0,
ȡ1,
D ȥ
e (f)(x) +
Ȣ0,
ȡ1,
D ȥ
d (f)(x) +
Ȣ0,
d l(f)(x)
D 1,
l
a
l
u
se f (x) w l
caso contrário.
se f (x) v l
se f (x) l
caso contrário
caso contrário
(1.32)
(1.33)
(1.34)
Ů K e x Ů E.
Def. 3.3 – E Ũ Z ; 0 E e 1 E mapeamentos de E em K 1 assumindo,
E
para todo f
n
2
respectivamente, 0 e 1.
a
d E (f)
para todo f
ŮK
dE
ȡ
+ ȥȢ10 ,,
D
E
E
E
1
.
a
de
K 1 E em K 1 E é definido por:
+
se f 0 E
caso contrário
(1.35)