1 UFBA 2003 - 2ª FASE - MATEMÁTICA – RESOLUÇÃO E

UFBA 2003 - 2ª FASE - MATEMÁTICA –
RESOLUÇÃO E COMENTÁRIOS POR PROFA. MARIA ANTÔNIA GOUVEIA.
Questão
01
(Valor: 10 pontos)
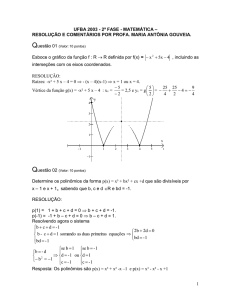
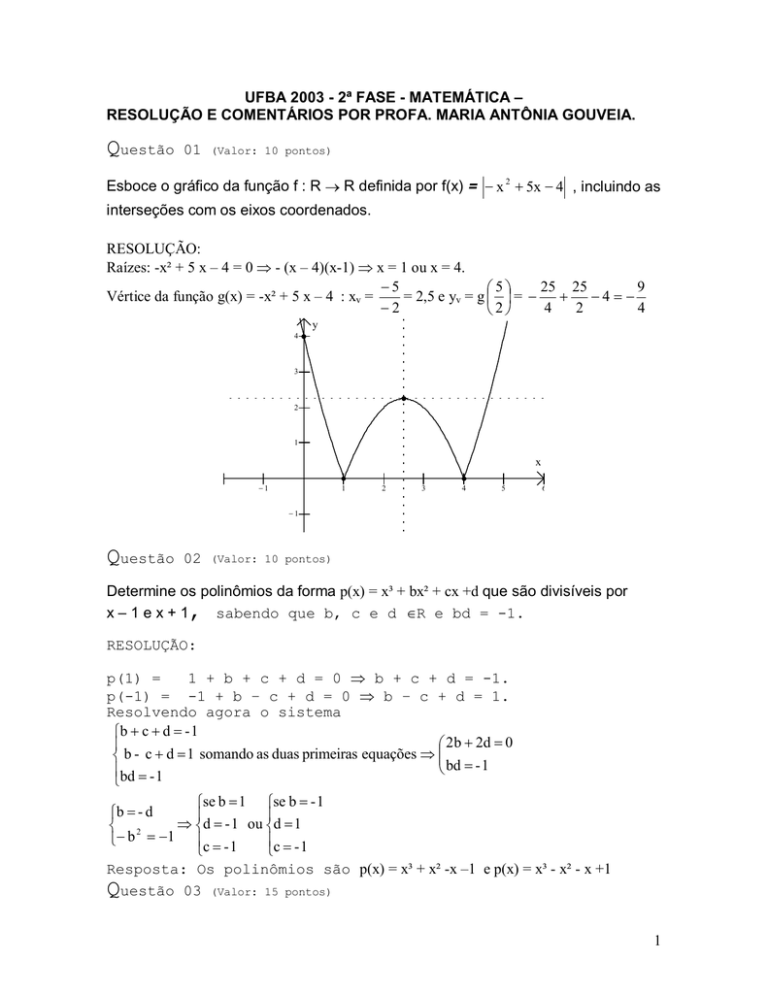
Esboce o gráfico da função f : R → R definida por f(x) = − x 2 + 5x − 4 , incluindo as
interseções com os eixos coordenados.
RESOLUÇÃO:
Raízes: -x² + 5 x – 4 = 0 ⇒ - (x – 4)(x-1) ⇒ x = 1 ou x = 4.
−5
25 25
9
5
= 2,5 e yv = g   = −
+
−4 = −
Vértice da função g(x) = -x² + 5 x – 4 : xv =
−2
4
2
4
2
4
y
3
2
1
x
−1
1
2
3
4
5
6
−1
Questão
02
(Valor: 10 pontos)
Determine os polinômios da forma p(x) = x³ + bx² + cx +d que são divisíveis por
x – 1 e x + 1, sabendo que b, c e d ∈R e bd = -1.
RESOLUÇÃO:
p(1) =
1 + b + c + d = 0 ⇒ b + c + d = -1.
p(-1) = -1 + b – c + d = 0 ⇒ b – c + d = 1.
Resolvendo agora o sistema
b + c + d = - 1
 2b + 2d = 0

 b - c + d = 1 somando as duas primeiras equações ⇒ 
 bd = - 1
bd = - 1

se b = 1 se b = - 1
b = - d


⇒ d = - 1 ou d = 1
 2
− b = −1 c = - 1
c = - 1


Resposta: Os polinômios são p(x) = x³ + x² -x –1 e p(x) = x³ - x² - x +1
Questão 03 (Valor: 15 pontos)
1
Determine uma equação da circunferência de centro (-1,2), sabendo que a
equação 3x + y – 9 =0 representa uma reta tangente a essa circunferência.
RESOLUÇÃO:
Se a reta é tangente á circunferência, então a distância do
centro (-1,2) à reta de equação
3x + y – 9 =0 é também a medida do raio da circunferência .
3(−1) + 1(2) − 9
− 10
10
Então R =
=
=
= 10 .
9 +1
10
10
A equação da circunferência é:
([ + ) + (\ − )
=
( )
⇒ [ + \ + [ − \ + + − = ⇒
[ + \ + [ − \ − = Resposta a equação é x 2 + y 2 + 2x − 4y − 5 = 0 .
Questão
04
(Valor: 15 pontos)
Considere os números complexos z = -1 +
3i
e
w=
3 + i e sejam A e B os pontos que representam, no plano cartesiano, os
z2
complexos zw e
, respectivamente.
w
A partir dessas informações, determine o cosseno do ângulo AOB, sendo O a
origem do plano cartesiano.
RESOLUÇÃO:
zw = − 1 + 3i 3 + i = - 2 3 + 2i ⇒ A = − 2 3 ,2
(
)( )
(
)
(- 1 + 3i) = (- 2 − 2 3i )( 3 − i) = − 4 3 − 4i - 3 − i ⇒ B = (−
z
=
w
4
( 3 + i )( 3 − i)
3+i
2
)
2
O segmento OA forma com o eixo dos x o
ângulo α, tal que
2
3
=−
⇒ α = 150°
tgα =
3
−2 3
O segmento OB forma com o eixo dos x o
ângulo β, tal que
1
3
tgβ =
=
⇒ β = 210°
3
3
Logo o ângulo AÔB mede 210°-150°=60°.
1
Assim o cos(AÔB) =
2
3 ,−1
$
β
α
2
%
2
Questão
05 (Valor: 20 pontos)
Deseja-se fabricar bandeirolas com perímetro de 50cm e
formato obtido retirando-se um semi-círculo de um retângulo
em que um dos lados, medindo 2r cm, coincide com o diâmetro
do semi-círculo retirado, conforme figura.
Nessas condições, determine o valor de r para o qual a área da
bandeirola é máxima.
RESOLUÇÃO:
O perímetro da bandeirola é igual AC+CD+BD + πr = 50 ⇒
2x + 2r + πr = 50 ⇒
50 - 2r - rπ
x=
⇒ a área de cada bandeirola será :
2
S = SABCD – Ssemi círculo
2
(3π + 4)r 2 + 50r
 50 - 2r - rπ  πr
S = 2r 
= −
−
2
2

 2
O valor de r para que a área seja máxima é
−E
− 50
50
r=
cm.
=
=
D
 3π + 4  3π + 4
2 −

2 

Questão
06
&
'
[
[
$
U
%
(Valor: 10 pontos)
3
A figura mostra a posição de um avião observado a partir de
dois pontos, A e B, localizados no solo e distantes 1km um
do outro. Sabe-se que, nesse instante, o avião dista,
respectivamente, 88 km e 9km, dos pontos A e B.
Nessas condições, determine a altura do avião, em relação
ao solo, no instante considerado
NP
NP
$ NP %
&
No triângulo AHC: h² = 88 - (1+x)².
No triângulo BHC: h² = 81 - x².
Assim 88 - (1+x)² = 81 - x² ⇒ 2x = 88 – 81 –
1 ⇒ x = 3.
Logo h² = 81 – 9 = 72 ⇒ h = 6 2 .
Resposta: Em relação ao solo a altura do avião
é de 6 2 km .
$
Questão
07
K
%
[
+
(Valor: 20 pontos)
.
Considere um cone circular reto, de altura igual a 9 u.c. e raio de base medindo
3 3 u.c., contendo esferas S1, S2, ..., Sn , ... Sabe-se que S1 está inscrita no cone e
que cada esfera, a partir da segunda, é tangente à anterior e à superfície lateral do
cone. Com base nessas informações, calcule a soma infinita dos volumes das
esferas.
RESOLUÇÃO:
4
&
U
3
4
)
0
U
&
U
(
1
*
'
U
2
2
U
$
'
U
U
+
Ö=
No triângulo retângulo HBC : tg %
U
%
$
%
3
Ö = ° ⇒ que o triângulo
= 3 ⇒%
3
ABC é eqüilátero e circunscrito ao círculo de raio r, então a sua altura HC = 3r ⇒ 3r = 9 ⇒
r = 3.
Os triângulos MCN, PCQ,....são também eqüiláteros.
1
Então como CG = 3 ⇒ r1 = 1 ⇒ que a altura do triângulo PCQ é igual a 1 ⇒ r2 = ,.....
3
1 1 1
1
As infinitas esferas têm raios ; 3, 1, , ,
,.... formando uma PG de razão .
3 9 27
3
Os volumes dessas esferas são:
3
4π 3 4π
4π  1  4π
3 1
  3
3
3  3 3
4π
4π 1
: 36π =
razão
3
3 36π
6
=
D1
1−T
=
=
3
4π 4π
4π
1
  = π que é uma PG de
3 81 2187
9
1
⇒ A soma dos volumes das infinitas esferas é
=
27
26 104π
π
= 36π =
.
27
3
5