CIRCUITOS INDUTIVOS Se numa tensão CA, v for aplicada a um

CEFET – BA – Vitória da Conquista
CIRCUITOS INDUTIVOS
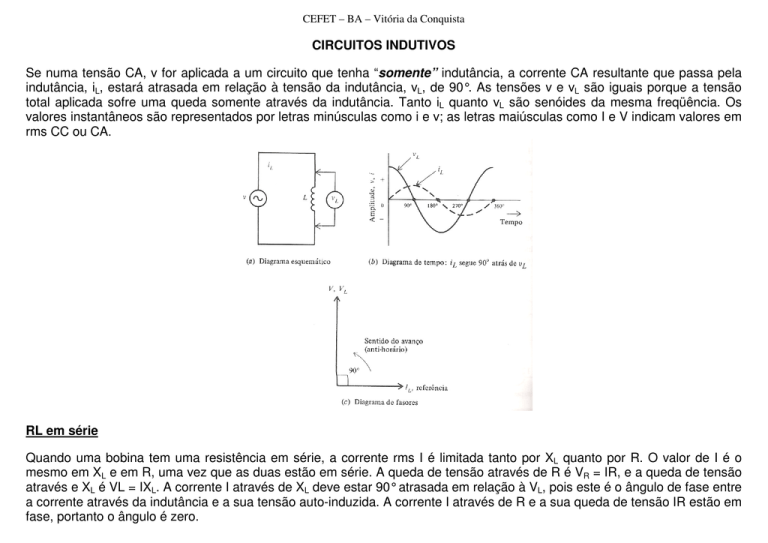
Se numa tensão CA, v for aplicada a um circuito que tenha “somente” indutância, a corrente CA resultante que passa pela
indutância, iL, estará atrasada em relação à tensão da indutância, vL, de 90°. As tensões v e vL são iguais porque a tensão
total aplicada sofre uma queda somente através da indutância. Tanto iL quanto vL são senóides da mesma freqüência. Os
valores instantâneos são representados por letras minúsculas como i e v; as letras maiúsculas como I e V indicam valores em
rms CC ou CA.
RL em série
Quando uma bobina tem uma resistência em série, a corrente rms I é limitada tanto por XL quanto por R. O valor de I é o
mesmo em XL e em R, uma vez que as duas estão em série. A queda de tensão através de R é VR = IR, e a queda de tensão
através e XL é VL = IXL. A corrente I através de XL deve estar 90° atrasada em relação à VL, pois este é o ângulo de fase entre
a corrente através da indutância e a sua tensão auto-induzida. A corrente I através de R e a sua queda de tensão IR estão em
fase, portanto o ângulo é zero.
Para associar duas formas de onda fora de fase, somamos seus fasores equivalentes. O método consiste em se acrescentar
a extremidade de um fasor a ponta da seta do outro, utilizando o ângulo para indicar a sua fase relativa. A soma dos fasores
produz um fasor resultante que parte da base de um fasor e vai até a extremidade da seta do outro. Como os fasores VR e VL
formam um ângulo reto, o fasor resultante é a hipotenusa de um triângulo retângulo. Da geometria de um triângulo retângulo,
o teorema de Pitágoras afirma que a hipotenusa é igual a raiz quadrada da soma dos quadrados dos catetos. Portanto, a
resultante fica
2
VT = VR + VL
2
onde a tensão total VT é o fasor soma das duas tensões VR e VL que estão 90° fora de fase. Todas as tensões devem ser
expressas nas mesmas unidades, sejam valores de rms, valores de pico, ou valores instantâneos. Por exemplo, quando VT
for um valor de rms, VR e VL também serão valores de rms. A maioria dos cáIcuIos em CA será dado em unidades de rms.
O ângulo de fase θ entre VT e VL é
Como VR está em fase com I, θ
também é o ângulo de fase entre
VT e I, onde I está atrasado em
relação a VT.
Impedância RL em série
A resultante da adição dos fasores R e XL é chamada de “impedância”. O símbolo que representa a impedância é Z. A
impedância é a reação total ao fluxo da corrente, expressa em ohms (Ω). O triângulo de impedância corresponde ao triângulo
de tensão, mas o fator comum I se cancela. As equações para a impedância e para o ângulo de fase são deduzidas da
seguinte forma:
RL em paralelo
Para circuitos paralelos contendo R e XL, a mesma tensão aplicada VT para através de R e XL pois ambas estão em paralelo
com VT. Não há diferença de fases entre estas tensões. Portanto, VT será usado como fasor de referência. A corrente no
ramo resistivo IR = VT/R está em fase com VT. A corrente no ramo indutivo IL = VT/XL está atrasada em relação à VT em 90°
porque a corrente numa indutância está atrasada em relação à tensão através dela de 90°. O fasor soma de IR e IL é igual a
corrente total da linha IT, ou
Exemplo: Um circuito CA com RL para paralelo tem uma tensão de pico de 100V aplicada através de R = 20Ω e XL = 20Ω.
Calcule IR, IL, IT e θ. Desenhe os diagramas de fasores e de tempo de vT, vR, iL e iT.
Como VT é o mesmo através de todo circuito em
paralelo, VT aparece como fasor de referência em
0°. IT está atrás de VT em 45°.
Impedância em paralelo
Para o caso geral do cálculo da impedância total ZT de R e XL em paralelo, suponha um número qualquer para a tensão
aplicada VT, pois no cálculo de ZT em função das correntes de ramo, o valor de VT se cancela. Um valor conveniente a ser
admitido para VT é o valor de R ou de XL, independentemente de qual seja o número mais alto. Este constitui apenas um
método entre outros que dão o valor de ZT.
Exemplo: Qual a impedância de ZT de um R de 200Ω em paralelo com XL de 400Ω? Suponha que a tensão aplicada VT seja
de 400V.
A impedância da associação de R de 200Ω em paralelo com XL de 400Ω é igual
a 178,6Ω, independentemente do valor da tensão aplicada. A impedância da
associação deve ser menor do que o menor número de ohms dos ramos em
paralelo. A impedância total de um circuito RL paralelo não é igual à do circuito
RL série; isto é
2
ZT ≠ R 2 + X L
porque a resistência e a reatância indutiva se combinam para apresentar uma
condição de carga diferente com relação à fonte de tensão.