Tamanho de amostras - geste

UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
ENGENHARIA MECÂNICA
ENG03108 - MEDIÇÕES TÉRMICAS
Energia e Fenômenos de Transporte
Prof. Paulo S. Schneider
www.geste.mecanica.ufrgs.br
[email protected]
Tamanho de amostras
Fundamentos
A capacidade de uma amostra de seguir uma distribuição estatística acaba determinando sua
classificação como grande ou pequena. As grandes amostras são aquelas onde se pode verificar a
densidade de probabilidade de forma definida, seguindo melhor as funções de distribuição adotadas,
o que não se verifica nas pequenas amostras.
Grandes amostras
Não há unanimidade na indicação do número de eventos que define uma grande amostra. A
norma ASHRAE 41.5-75 (1975) indica 20 eventos (n>20), enquanto que Triola (1998) já indica 30
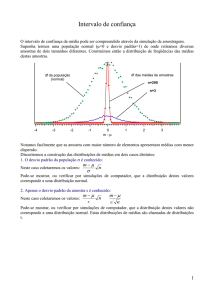
eventos (n>30). Isso se deve ao comportamento dos níveis de confiança associados ao valor do desvio padrão σ em função do número de graus de liberdade ν, que passa a variar de forma importante
quando o número de eventos é inferior ao valor limite citado acima. Esse comportamento é mostrado na figura 1
Figura 1- Níveis de confiança P em função dos graus de liberdade ν (Fonte: Vuolo, 1998)
_
Nas grandes amostras, o valor médio x é a melhor estimativa da média populacional µ, ou
valor verdadeiro. Associa-se ao valor da média um intervalo de confiança, ou incerteza, que obedece a uma dada probabilidade.
Medições Térmicas – Universidade Federal do Rio Grande do Sul - Prof. Paulo Schneider
As equações aplicáveis para grandes e pequenas amostras são:
média aritmética
x=
∑x
i
n
desvio padrão para grandes amostras
 ( x − x )2 
σ =  ∑ i

n


(1)
1/ 2
(2)
e o desvio padrão experimental ou convencional
 ∑ ( xi − x ) 2 
s=


n −1


1/ 2
(3)
Quando consider-se uma grande amostra, a determinação do seu tamanho é dada pelo cálculo da incerteza da média
u_ =
x
kσ
n
(4)
Dela pode-se isolar o valor do número de eventos n, tal que

 kσ
n=
 u_
 x




2
(5)
Pequenas amostras- distribuição t de Student
Para amostras com número de eventos inferior a 30 ou mesmo 20, o valor do desvio padrão
não é mais conhecido estatisticamente, e passa-se a empregar a Equação 3, onde o número de eventos do denominador n-1 é conhecido por graus de liberdade ν. A subtração de um evento numa pequena amostra pode ser compreendida pelo fato que a média é empregada para o cálculo de grandezas estatísticas, e portanto está comprometida.
Como o desvio padrão não é conhecido, não estamos mais tratando com uma distribuição
gaussiana. A distribuição que melhor se adapta para esse caso é a distribuição t de Student, desenvolvida por William Gosset (1876-1937) que trabalhava para a cervejaria Guinness. Essa distribuição tem as seguintes propriedades
•
•
•
varia conforme o nº de eventos
tem forma simétrica (sino)
aproxima-se da distribuição de Gauss para ν > 30
A incerteza do valor médio de uma pequena amostra é dada por
Medições Térmicas – Universidade Federal do Rio Grande do Sul - Prof. Paulo Schneider
u_ =
x
ts
n
(6)
onde t é o valor da distribuição para uma dada confiabilidade e um número de graus de liberdade ν,
s o desvio para um número de graus de liberdade ν, e n é o número total de eventos da amostra.
Tabela 3 - Valores de t-student para diferentes níveis de confiabilidade
Nível de confiabilidade
ν
68,27%
95,45%
99,73%
1
1,84
13,97
235,80
2
1,32
4,53
19,21
3
1,20
3,31
9,22
4
1,14
2,87
6,62
5
1,11
2,65
5,51
6
1,09
2,52
4,90
7
1,08
2,43
4,53
8
1,07
2,37
4,28
9
1,06
2,32
4,09
10
1,05
2,28
3,96
15
1,03
2,18
3,59
20
1,03
2,13
3,42
25
1,02
2,11
3,33
30
1,02
2,09
3,27
40
1,01
2,06
3,20
50
1,01
2,05
3,16
1,00
2,00
3,00
∞
Deve-se observar que com este procedimento, ao se estimar a incerteza de medição, na realidade o que se faz é estimar o desvio padrão da população a partir do desvio padrão da amostra,
que subestima o primeiro. O valor estimado, portanto, é o que se deve usar em futuras medições,
com um número infinito de graus de liberdade.
A média da distribuição, também chamada de momento de la ordem, pode ser teoricamente
calculada quando o número de termos da população é muito grande. O mesmo acontece para o desvio padrão, também chamado de momento de 2a ordem . Entretanto, para os casos reais, a amostra é
finita e o número de termos é pequeno. Deve-se, portanto, determinar os parâmetros estatísticos de
medição a partir de um número pequeno de valores. Assim, a média será estimada e não determinada. Novamente, a estatística mostra que a melhor estimativa da média ( x ) e do desvio padrão da
amostra (s) são dadas respectivamente pelas expressões 1 e 3 já apresentadas. A média na Equação
1 pode ser determinada minimizando o valor de s na Eq. (3), em relação a ( x ) , isto é, diferenciando
s em relação a ( x ) , e igualando a zero.
Medições Térmicas – Universidade Federal do Rio Grande do Sul - Prof. Paulo Schneider
Exercícios
1- Uma dada substância na fase líquida encontra-se em equilíbrio térmico em um banho termostático. Sua temperatura é medida por um termômetro de exatidão de ±0,5 ºC, informado pelo seu fabri_
cante. Quantas medidas serão necessárias para que se possa dizer que a temperatura média t dessa
_
_
substância será expressa como t = t ± 0,2 º C , com 5% de nível de significância (ou 95% de confiança)?
a) Trate o problema como se fosse uma grande amostra
b) Trate agora o problema como uma pequena amostra
2- Deseja-se expressar o valor médio de uma medida de temperatura realizada com o termopar tipo
K (ver folha de dados a seguir) com aproximadamente 100% de probabilidade para a faixa de
120ºC, com metade da incerteza que o sensor exibe para essa faixa.
a) Quantas medidas seriam necessárias, empregando a noção de média de grande amostra?
b) Caso o valor encontrado para n seja inferior a 20 eventos, esse resultado caracteriza a pequena
amostra. Caso não se disponha de uma tabela para cálculo de pequenas amostras, indique o que devia mudar no resultado de grande amostra para que ele pudesse representar o de pequena amostra.
c) Agora, faça esse cálculo e compare o resultado com aquela estimado em b)