Lógica Matemática Elementos de Lógica Digital
Lógica Proposicional (cont.)
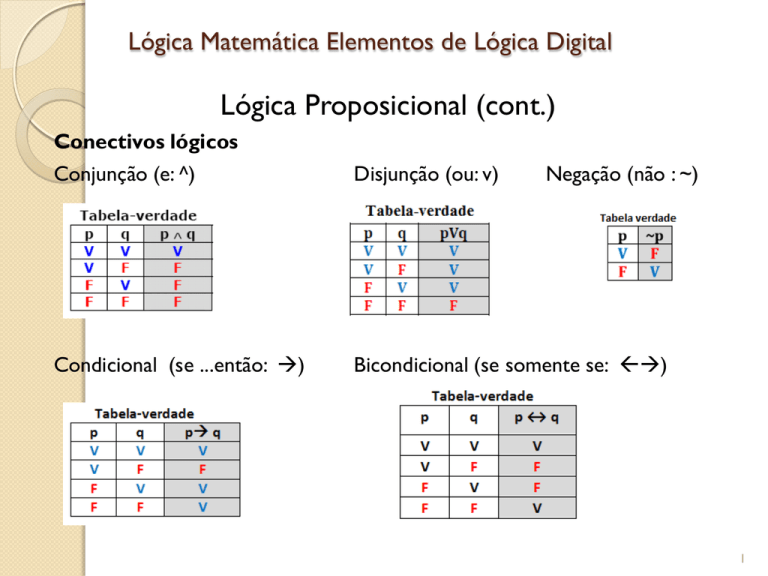
Conectivos lógicos
Conjunção (e: ^)
Disjunção (ou: v)
Condicional (se ...então: )
Bicondicional (se somente se: )
Negação (não : ~)
1
Lógica Matemática Elementos de Lógica Digital
Negação de um proposição composta
Negar uma proposição simples.
p: João é médico.
~p: João não é médico. Ou ~p: É falso que João é médico
Como negar uma proposição composta?
Vai depender da estrutura da proposição.
2
Lógica Matemática Elementos de Lógica Digital
Negação de uma proposição conjuntiva: ~(p e q)
w: João é médico e Pedro é analista
p: João é médico q: Pedro é analista
~p: João não é médico ~q: Pedro não é analista
Em linguagem lógica: ~(p ^ q) = ~p v ~q
p
q
p^q ~p ~q
(~p)^(~q)
~(p^q)
pvq
(~p)v(~q)
V
V
V
F
F
F
F
V
F
V
F
F
F
V
F
V
V
V
F
V
F
V
F
F
V
V
V
F
F
F
V
V
V
V
F
V
~w: João não é médico ou Pedro não é analista
3
Lógica Matemática Elementos de Lógica Digital
Negação de uma proposição disjuntiva: ~(p ou q)
w: Pedro não é dentista ou Paulo é engenheiro
p: Pedro não é dentista q: Paulo é engenheiro
~p: Pedro é dentista
~q: Paulo não é engenheiro
Em linguagem lógica: ~(p v q) = ~p ∧~q
p
q
pvq ~p ~q
(~p)v(~q)
~(pvq)
p^q
~p ^ ~q
V
V
V
F
F
F
F
V
F
V
F
V
F
V
V
F
F
F
F
V
V
V
F
V
F
F
F
F
F
F
V
V
V
V
F
V
~w: Pedro é dentista e Paulo não é engenheiro.
4
Lógica Matemática Elementos de Lógica Digital
Negação de uma proposição condicional: ~(p q)
w: Se chover, então levarei o guarda-chuva
p: se chover
q: levarei o guarda-chuva
~p: chove
~q: não levarei o guarda-chuva
Em linguagem lógica: ~(p q) = p ∧~q
p q pq ~p
~q
~(pq)
~p~q
~pq
p~q
p^~q
V V
V
F
F
F
V
V
F
F
V F
F
F
V
V
V
V
V
V
F
v
V
V
F
F
F
V
V
F
F
F
V
V
V
F
V
F
V
F
~w: Chove e eu não levo o guarda-chuva
5
Lógica Matemática Elementos de Lógica Digital
Negação do bicondicional: ~(p↔q)
w: trabalharei se somente se ganhar salário
p: trabalharei q: ganhar salário
~p: não trabalharei ~q: não ganho salário
Em linguagem lógica:
~(p q) = [(p e ~q) ou (q e ~p)]
p
q
~p
~q
pq
~(pq)
A= p^~q
B= q^~p
AvB
V
V
F
F
V
F
F
F
F
V
F
F
V
F
V
V
F
V
F
V
V
F
F
V
F
V
V
F
F
V
V
V
F
F
F
F
~w: não trabalharei se somente se não ganho salário
6
Lógica Matemática Elementos de Lógica Digital
Ordem de precedência dos conectivos lógicos.
Primeiramente obedece os delimitadores, {[( )]} depois
segue a ordem:
1º negação (~)
2º conjunção e disjunção ( , )
3º implicação ( )
4º bicondicional ( )
7
Lógica Matemática Elementos de Lógica Digital
Exemplo:
F(p,q,r)=(p ∧ ~q) (q v ~r)
Lê-se: Se p e não q, então q ou não r
8
Lógica Matemática Elementos de Lógica Digital
Tabela verdade
Trata-se de uma tabela mediante a qual são analisados
os valores lógicos de proposições compostas.
1 proposição = 2 combinações (V , F)
2 proposições = 4 combinações (VV, VF, FV, FF)
3 proposições = 8 combinações
(VVV,VVF,VFV,VFF, FVV, FVF, FFV, FFF)
...
N proposições = 2N combinações
Assim:
Nº linhas da Tabela-Verdade = 2 nº de proposições
9
Lógica Matemática Elementos de Lógica Digital
Tautologia
Uma proposição composta formada por duas ou mais
proposições p, q, r, ... será dita uma Tautologia se ela for
sempre verdadeira, independentemente dos valores lógicos
das proposições p, q, r, ... que a compõem.
A proposição (p ∧ q) (p V q) é uma tautologia
Ex.: F(p,q,s)=[(p v q) ∧ (p ∧ s)] p, verifique se é uma
Tautologia.
10
Lógica Matemática Elementos de Lógica Digital
Contradição
Uma proposição composta formada por duas ou mais
proposições p, q, r, ... será dita uma contradição se ela
for sempre falsa, independentemente dos valores
lógicos das proposições p, q,r ... que a compõem.
A proposição “ p ↔ ~p ” é uma contradição
11
Lógica Matemática Elementos de Lógica Digital
Contingência
Uma proposição composta será dita uma contingência
sempre que não for uma tautologia ou uma
contradição.
A proposição “p ↔ (p∧q)” é uma contingência.
12
Lógica Matemática Elementos de Lógica Digital
Equivalência Lógica
De acordo com os valores lógicos que as proposições
compostas assumem, em suas possíveis interpretações, elas
podem ser classificadas em vários tipos:
se a expressão assume sempre o valor V, em qualquer
interpretação, é chamada uma tautologia, ou uma expressão
válida;
se a expressão assume o valor V em alguma interpretação,
é dita satisfatível, ou consistente; evidentemente, as
tautologias são exemplos de expressões satisfatíveis;
se a expressão assume sempre o valor F, em qualquer
interpretação, é chamada uma contradição, ou uma
expressão insatisfatível, ou inconsistente.
se a expressão assume o valor F em alguma interpretação,
é chamada uma expressão inválida; claramente, as
contradições são, também, expressões inválidas;
13
Lógica Matemática Elementos de Lógica Digital
Exercícios fixação
1) Dê o valor lógico das proposições
a) (8>2) ^(4 ≤4)
b) (6< 10).(6> ⅓)
c) (7<2) +[(4-3)≥1]
d) (5>8) (4>3)
e) (4<2) + (2<4)
f) (8-3 = 5) (2≤ 2)
g) (8-10=2) (6-2=4)
h) (4-2)(8-2=15)
i) ~(4 >5) ^ (⅕ > ⅓)
14
Lógica Matemática Elementos de Lógica Digital
2) A proposição “ Se Marcos não estuda, então Pedro não
passeia” equivale dizer:
a)
b)
c)
d)
e)
Marcos estudar é condição necessária para Pedro não
passear
Marcos estudar é condição suficiente para Pedro não
passear
Marcos não estudar é condição necessária para Pedro
não Passear
Marcos não estudar é condição suficiente para Pedro
passear
Marcos estudar é condição suficiente para Pedro
passear
15
Lógica Matemática Elementos de Lógica Digital
3) Sejam as proposições:
“p: Está frio” e “q: Está chovendo”.
Traduzir para linguagem corrente as seguintes proposições:
a) ~p
b) p.q
c) p+q
d) p q
e) p~q
f) p v ~q
g) ~p^~q
h) ~~q
16
Lógica Matemática Elementos de Lógica Digital
4) Verifique se as afirmações dadas são
suficientes para determinar o valor da
expressão:
a) (p q) r , onde r tem valor lógico V
b) (p+r)+(sq), onde q tem valor lógico F
c) [(p+q)(p.q)] [(r.p)+q], onde q tem
valor lógico V
d) [(pq) p], onde q tem valor lógico V
17
Lógica Matemática Elementos de Lógica Digital
5) Considerando Vl(p)=F; Vl(q)=V; Vl(x)=F e
Vl(y)=V, determine:
a)
b)
c)
Vl([(p+q).(x+y)]p)=
Vl(x.yp)=
Vl(p.y.p.x)=
18
Lógica Matemática Elementos de Lógica Digital
Sistemas dicotômicos
19
Lógica Matemática e Elementos de Lógica Digital
Sistemas dicotômicos
Chama-se interruptor ao dispositivo ligado a um ponto de
um circuito elétrico que pode assumir um dos dois
estados:
Fechado (1)
Aberto (0)
Quando fechado o interruptor permite que a corrente
passe através do ponto. Quando aberto nenhuma
corrente pode passar através do ponto.
Representação:
Lógica Matemática e Elementos de Lógica Digital
Sejam a e b dois interruptores ligados em paralelo. Numa
ligação em paralelo só passará corrente se pelo menos um
dos interruptores estiver fechado.
Denotamos um circuito em paralelo por “a+b”
Essa ligação descreve a seguinte tabela:
a
b
a+b
1
1
1
1
0
1
0
1
1
0
0
0
Observe que essa tabela é
equivalente a proposição
“ou” da lógica proposicional
Lógica Matemática e Elementos de Lógica Digital
Sejam a e b dois interruptores ligados em série. Numa
ligação em serie só passará corrente se ambos
interruptores estiverem fechados.
Denotamos um circuito em série por “a.b”
Essa ligação descreve a seguinte tabela:
a
b
a . b
1
1
1
1
0
0
0
1
0
0
0
0
Observe que essa tabela é
equivalente a proposição “e”
da lógica proposicional
Lógica Matemática e Elementos de Lógica Digital
Se um interruptor apresenta aberto quando “a” fechado e
apresenta fechado quando “a” aberto, chamamos de
inversão (negação) e denotamos por “~a” ou “
“.
A tabela verdade
a
~ a
1
0
0
1
Equivale a negação da lógica proposicional
Lógica Matemática e Elementos de Lógica Digital
Com a combinação de interruptores podemos criar
expressões mais complexas
Ex.
S = a.(b+c) + a’.(b’+c’)
Cuja tabela é ...
Lógica Matemática e Elementos de Lógica Digital
Descreva as expressões dada pelos circuitos
S=
S=
Lógica Matemática e Elementos de Lógica Digital
Desenhe os circuito dado pelas expressões:
a)
p.(q’.(s+r)+r.s)+(q+p’).(r.s’+s)
b)
a. (b+c+d)
Próxima aula: Circuitos digitais












