Regras da deduç˜ao e tabelas de verdade 1 Lógica - Inf

Instituto de Informática
Departamento de Informática Teórica
2006/2
Prof. Marcus Ritt
Regras da dedução e tabelas de verdade
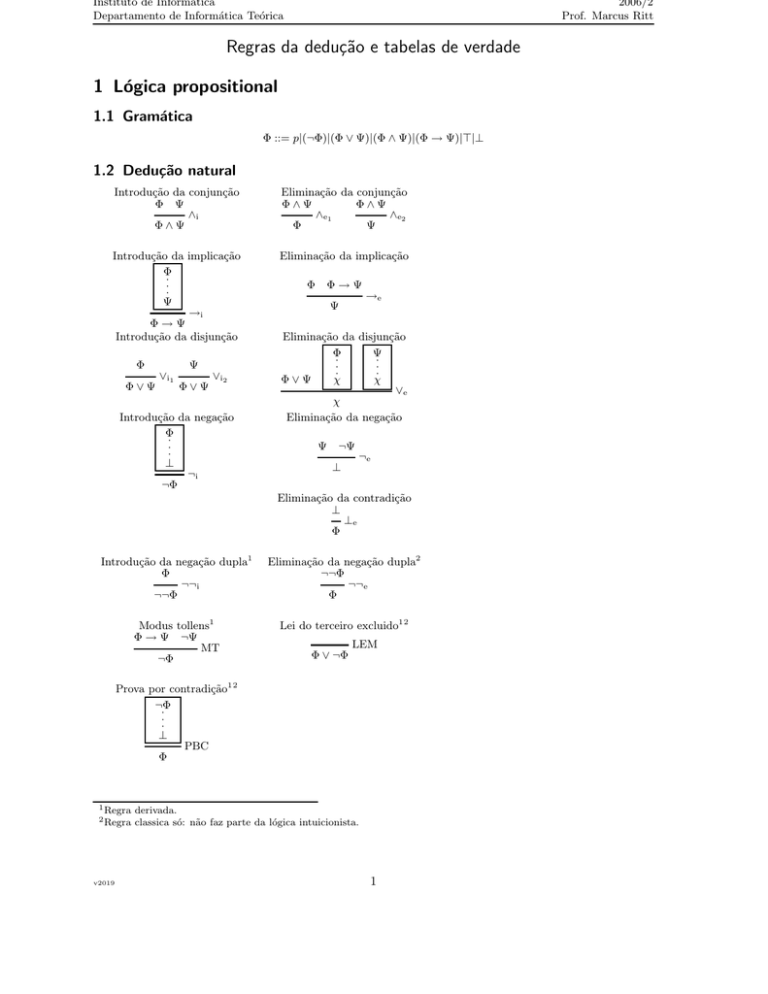
1 Lógica propositional
1.1 Gramática
Φ ::= p|(¬Φ)|(Φ ∨ Ψ)|(Φ ∧ Ψ)|(Φ → Ψ)|>|⊥
1.2 Dedução natural
Introdução da conjunção
Φ Ψ
∧i
Φ∧Ψ
Eliminação da conjunção
Φ∧Ψ
Φ∧Ψ
∧ e1
∧ e2
Φ
Ψ
Introdução da implicação
Φ
·
·
·
Ψ
→i
Φ→Ψ
Introdução da disjunção
Eliminação da implicação
Φ
Φ∨Ψ
∨ i1
Ψ
Φ∨Ψ
∨ i2
Introdução da negação
Φ
·
·
·
⊥
¬i
¬Φ
Φ
Φ→Ψ
Ψ
→e
Eliminação da disjunção
Φ
Ψ
·
·
·
·
·
·
χ
χ
Φ∨Ψ
∨e
χ
Eliminação da negação
Ψ
¬Ψ
⊥
¬e
Eliminação da contradição
⊥
⊥e
Φ
Introdução da negação dupla1
Φ
¬¬i
¬¬Φ
Eliminação da negação dupla2
¬¬Φ
¬¬e
Φ
Modus tollens1
Φ → Ψ ¬Ψ
MT
¬Φ
Lei do terceiro excluido1 2
Φ ∨ ¬Φ
LEM
Prova por contradição1 2
¬Φ
·
·
·
⊥
PBC
Φ
1 Regra
2 Regra
v2019
derivada.
classica só: não faz parte da lógica intuicionista.
1
Instituto de Informática
Departamento de Informática Teórica
2006/2
Prof. Marcus Ritt
1.3 Semântica: Tabelas de verdade
Conjunção
Φ Ψ Φ∧Ψ
f
f
f
f
v
f
v
f
f
v
v
v
Negação
Φ ¬Φ
f
v
v
f
Disjunção
Φ Ψ Φ∨Ψ
f
f
f
f
v
v
v
f
v
v
v
v
Falsidade
Implicação
Φ Ψ Φ→Ψ
f
f
v
f
v
v
v
f
f
v
v
v
Verdade
⊥
f
>
v
1.4 Árvores de refutação
Conjunção
Conjunção negada
¬(a ∧ b)
a∧b
a
¬a
Negação dupla
¬¬a
HH
HH
HH
HH
H#
v
vv
vv
v
v
v
{v
¬b
a
b
Disjunção
a ∨ bC
a
{{
{{
{
{
}{
{
CC
CC
CC
C!
b
a→D
b
¬a
Negação
¬a
¬a
a
×
¬b
Implicação negada
¬(a → b)
Implicação
x
xx
xx
x
x
{x
x
Disjunção negada
¬(a ∨ b)
DD
DD
DD
DD
"
b
a
¬b
v2019
2
Instituto de Informática
Departamento de Informática Teórica
2006/2
Prof. Marcus Ritt
2 Lógica de predicados
2.1 Gramática
t ::= v|c|f (t1 , t2 , . . . , tn )
Φ ::= p(t1 , . . . , tn )|(¬Φ)|(Φ ∨ Ψ)|(Φ ∧ Ψ)|(Φ → Ψ)|(∀vΦ)|(∃vΦ)|>|⊥
2.2 Dedução natural
Axioma de identidade
Substituição
t1 = t 2
Φ[t1/x]
=i
t=t
Φ[t2 /x]
Eliminação da quantificação universal
∀xΦ
∀xe
Φ[t/x]
Eliminação da quantificação existencial1
x0
Φ[x0 /x]
·
·
·
∃xΦ
χ
∃xe
χ
=e
Introdução da quantificação universal 1
x0
·
·
·
Φ[x0 /x]
∀xi
∀xΦ
Introdução da quantificação existencial
Φ[t/x]
∃xΦ
∃xi
2.3 Árvores de refutação
Quantificação universal
Quantificação universal negada
∀xΦ
¬∀xΦ
Φ[t/x]
∃x¬Φ
Se aplica várias vezes.
t preferencialmente com constantes existentes.
Quantificação existencial
Quantificação existencial negada
∃xΦ
¬∃xΦ
Φ[t/x]
∀x¬Φ
Novos constantes em t.
Identidade
t1 = t 2
Identidade negada
¬t = t
×
Φ[t1 /x]
Φ[t2 /x]
1x
0
v2019
é uma variável que ainda não ocorreu na prova
3