CIRCUITOS DE DUAS PORTAS QUADRIPOLOS

Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
CIRCUITOS DE DUAS PORTAS
QUADRIPOLOS
NOTAS DE AULA (CAP. 19 – LIVRO DO NILSON)
0. CONSIDERAÇÕES INICIAIS
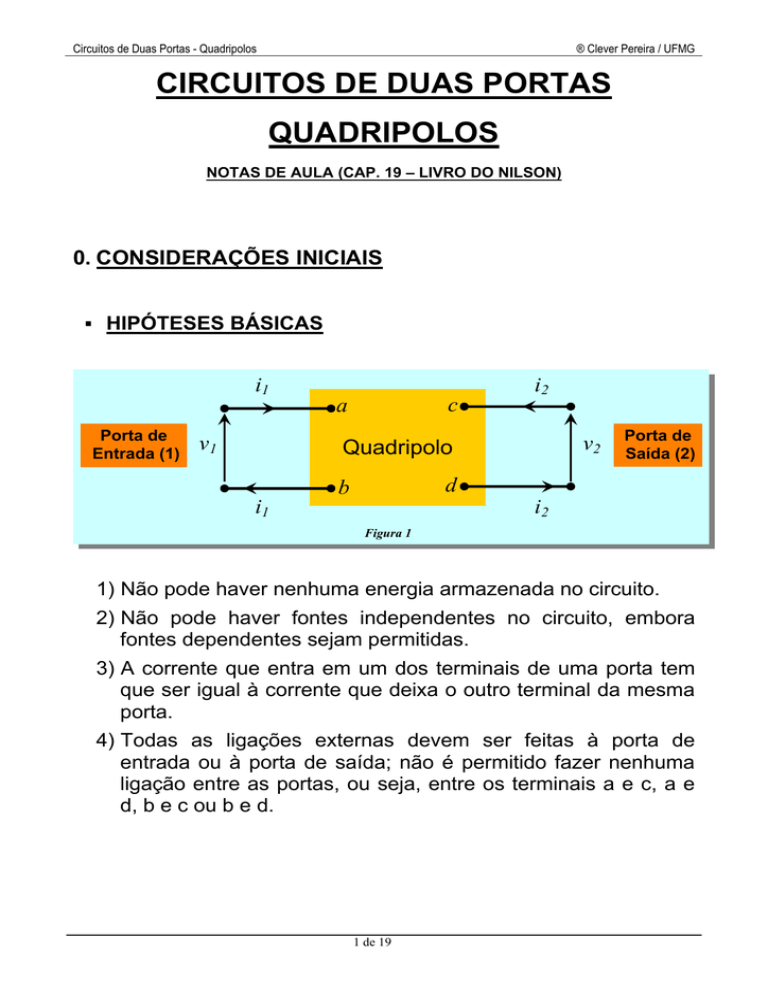
ƒ HIPÓTESES BÁSICAS
i1
c
a
Porta de
Entrada (1)
v1
i2
v2
Quadripolo
Porta de
Saída (2)
d
b
i1
i2
Figura 1
1) Não pode haver nenhuma energia armazenada no circuito.
2) Não pode haver fontes independentes no circuito, embora
fontes dependentes sejam permitidas.
3) A corrente que entra em um dos terminais de uma porta tem
que ser igual à corrente que deixa o outro terminal da mesma
porta.
4) Todas as ligações externas devem ser feitas à porta de
entrada ou à porta de saída; não é permitido fazer nenhuma
ligação entre as portas, ou seja, entre os terminais a e c, a e
d, b e c ou b e d.
1 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
1. MODELOS
I1
Porta de
Entrada (1)
I2
c
a
Quadripolo
Dom. Freq.
V1
Porta de
Saída (2)
d
b
I1
V2
I2
Figura 2
Parâmetros de Quadripolos
1.1. Parâmetros IMITÂNCIA
(a) Parâmetros Impedância
i⋅I
V =Z
→
⎡V1 ⎤ ⎡ z11
⎢V ⎥ = ⎢ z
⎣ 2 ⎦ ⎣ 21
z12 ⎤ ⎡ I1 ⎤
⋅
z22 ⎥⎦ ⎢⎣ I 2 ⎥⎦
(1)
y12 ⎤ ⎡V1 ⎤
⋅
y22 ⎥⎦ ⎢⎣V2 ⎥⎦
(2)
(b) Parâmetros Admitância
I = Yi ⋅ V
→
⎡ I1 ⎤ ⎡ y11
⎢I ⎥ = ⎢ y
⎣ 2 ⎦ ⎣ 21
1.2. Parâmetros de TRANSMISSÃO
(a) Parâmetros A
⎡V1 ⎤ i ⎡ V2 ⎤
⎢ I ⎥ = A ⋅ ⎢− I ⎥
⎣ 1⎦
⎣ 2⎦
→
⎡V1 ⎤ ⎡ a11
⎢ I ⎥ = ⎢a
⎣ 1 ⎦ ⎣ 21
a12 ⎤ ⎡ V2 ⎤
⋅
a22 ⎥⎦ ⎢⎣ − I 2 ⎥⎦
(3)
→
⎡V2 ⎤ ⎡ b11 b12 ⎤ ⎡ V1 ⎤
⎢ I ⎥ = ⎢b
⎥ ⋅ ⎢−I ⎥
b
⎣ 2 ⎦ ⎣ 21 22 ⎦ ⎣ 1 ⎦
(4)
(b) Parâmetros B
⎡V2 ⎤ i ⎡ V1 ⎤
⎢ I ⎥ = B ⋅ ⎢−I ⎥
⎣ 2⎦
⎣ 1⎦
2 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
1.3. Parâmetros HÍBRIDOS
(a) Parâmetros H
⎡V1 ⎤ i ⎡ I1 ⎤
⎢ I ⎥ = H ⋅ ⎢V ⎥
⎣ 2⎦
⎣ 2⎦
→
⎡V1 ⎤ ⎡ h11
⎢ I ⎥ = ⎢h
⎣ 2 ⎦ ⎣ 21
h12 ⎤ ⎡ I1 ⎤
⋅
h22 ⎥⎦ ⎢⎣V2 ⎥⎦
(5)
→
⎡ I1 ⎤ ⎡ g11
⎢V ⎥ = ⎢ g
⎣ 2 ⎦ ⎣ 21
g12 ⎤ ⎡V1 ⎤
⋅
g 22 ⎥⎦ ⎢⎣ I 2 ⎥⎦
(6)
(b) Parâmetros G
⎡ I1 ⎤ i ⎡V1 ⎤
⎢V ⎥ = G ⋅ ⎢ I ⎥
⎣ 2⎦
⎣ 2⎦
2. DETERMINAÇÃO DOS PARÂMETROS IMPEDÂNCIA
Expandindo as equações (1) vem que
⎧ V1 = z11 I1 + z12 I 2
⎨
⎩ V2 = z21 I1 + z22 I 2
(7)
Desta forma, pode-se definir os parâmetros impedância da
seguinte forma:
Z11 =
z12 =
z21 =
z22 =
V1
I1
V1
I2
V2
I1
V2
I2
Impedância do ponto de vista da porta 1 com a porta 2 aberta
I2 =0
Impedância de transferência, definida como a relação entre a tensão na
porta 1 e a corrente na porta 2 com a porta 1 aberta.
I1 = 0
I2 =0
Impedância de transferência, definida como a relação entre a tensão na
porta 2 e a corrente na porta 1 com a porta 2 aberta.
Impedância do ponto de vista da porta 2 com a porta 1 aberta.
I1 = 0
3 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Exemplo: Determinar os parâmetros z
do circuito ao lado.
Sabe-se que
I1
5Ω
V1
⎡V1 ⎤ ⎡ z11
⎢V ⎥ = ⎢ z
⎣ 2 ⎦ ⎣ 21
z12 ⎤ ⎡ I1 ⎤
⋅
z22 ⎥⎦ ⎢⎣ I 2 ⎥⎦
I2
20 Ω
15 Ω
V2
(8)
Figura 3
Então
z11 =
z12 =
z21 =
z22 =
V1
I1
V1
I2
V2
I1
V2
I2
20 ⋅ 20
= 10 Ω
20 + 20
(9)
20
V2
25
=
= 7,5 Ω
V2
9,375
(10)
15
V1
20
=
= 7,5 Ω
V1
10
(11)
=
I2 =0
I1 = 0
I 2 =0
=
I1 = 0
15 ⋅ 25
= 9,375 Ω
15 + 25
(12)
3. RELAÇÃO ENTRE OS PARÂMETROS DE UM QUADRIPOLO
3.1. Relação entre os parâmetros z e os parâmetros y
São válidas as seguintes equações para quadripolos em termos
dos parâmetros z e y:
⎧
⎪
⎪
⎨
⎪
⎪
⎩
⎡V1 ⎤ ⎡ z11
⎢V ⎥ = ⎢ z
⎣ 2 ⎦ ⎣ 21
z12 ⎤ ⎡ I1 ⎤
⋅
z22 ⎦⎥ ⎣⎢ I 2 ⎦⎥
⎡ I1 ⎤ ⎡ y11
⎢I ⎥ = ⎢ y
⎣ 2 ⎦ ⎣ 21
y12 ⎤ ⎡V1 ⎤
⋅
y22 ⎥⎦ ⎢⎣V2 ⎥⎦
(13)
4 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Pode-se notar pelas equações (13) que
⎡ y11
⎢y
⎣ 21
y12 ⎤ ⎡ z11
=
y22 ⎥⎦ ⎢⎣ z21
z12 ⎤
z22 ⎥⎦
−1
(14)
Resolvendo (14) vem que
⎡ y11
⎢y
⎣ 21
⎡ z22 − z12 ⎤
y12 ⎤ ⎣⎢ − z21 z11 ⎦⎥
=
=
y22 ⎥⎦
∆z
⎡ z22
⎢
⎣ − z21
z11
z21
− z12 ⎤
z11 ⎦⎥
z12
z22
(15)
Exemplo: Determinar os parâmetros y do circuito do exemplo
anterior
No exemplo anterior foram determinados os parâmetros z do
quadripolo definido pelo circuito elétrico da figura 1, dados por
7,5 ⎤
i = ⎡ 10
Z
⎢7,5 9,375⎥ Ω
⎣
⎦
(16)
Desta forma
⎡9, 375 −7, 5⎤
−1
⎢ −7, 5
⎥
10
7,
5
10
⎡
⎤
⎣
⎦=
Yi = ⎢
=
⎥
10
7, 5
⎣7, 5 9, 375⎦
7, 5 9, 375
⎡9, 375 −7, 5⎤
⎢ −7, 5
10 ⎥⎦ ⎡ 0, 25 −0, 20 ⎤
⎣
=
=⎢
⎥ S
37, 5
⎣ −0, 20 0, 2667 ⎦
5 de 19
(17)
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
4. ANÁLISE DE CIRCUITOS
TERMINAÇÕES
DE
DUAS
PORTAS
COM
A figura 4 abaixo mostra um quadripolo com terminações Vg, Zg e
ZL.
Zg
+
Vg
I1
c
a
I2
Quadripolo
Domínio da
Freqüência
V1
−
V2
ZL
d
b
I1
I2
Figura 4
Tal tipo de quadripolo pode ser analisado através do cálculo de
seis características principais:
1. Impedância de entrada Z in = V1 I1 ou admitância de entrada Yin = I1 V1 ;
2. Corrente de saída I2;
3. Tensão e impedância de Thévenin (VTh e ZTh) do ponto de vista da
porta 2;
4. Ganho de corrente I 2 I1 ;
5. Ganho de tensão V2 V1 ;
6. Ganho de tensão V2 Vg .
5. DETERMINAÇÃO DAS CARACTERÍSTICAS DE CIRCUITOS
DE DUAS PORTAS EM FUNÇÃO DOS PARÂMETROS z
As equações (18) estabelecem as relações entre as grandezas
terminais de um quadripolo, descrito pelos seus parâmetros z e
pelos parâmetros da fonte Vg, Zg e da carga ZL.
⎧ V1 = z11 I1 + z12 I 2
⎪V = z I + z I
⎪ 2
21 1
22 2
⎨
⎪ V1 = Vg − Z g I1
⎪ V = −Z I
⎩ 2
L 2
(18)
6 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
A impedância de entrada vista da porta 1 Zin(1) é dada pela
relação
Z in (1) =
V1
I1
(19)
Da equação (18.b) vem que
I2 =
V2 − z21 I1
z22
(20)
Substituindo (18.d) em (20) resulta em
I2 =
− Z L I 2 − z21 I1
z22
(21)
z21
I1
z22 + Z L
(22)
Ou seja
I2 = −
Substituindo (22) em (18.a) vem que
V1 = z11 I1 + z12 I 2 = z11 I1 − z12
z21
I1
z22 + Z L
(23)
Ou
Z in (1) =
V1
z21
= z11 − z12
I1
z22 + Z L
(24)
Ou também que
Z in (1) =
V1 ∆z + z11Z L
=
I1
z22 + Z L
(25)
A corrente I2 pode ser obtida substituindo (18.c) e (18.d) nas
equações (18.a) e (18.b), ou seja
⎧ Vg − Z g I1 = z11 I1 + z12 I 2
⎨
⎩ − Z L I 2 = z21 I1 + z22 I 2
(26)
7 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Rearranjando os termos em (26) resulta que
⎧⎪ ( z11 + Z g ) I1 + z12 I 2 = Vg
⎨
⎪⎩ z21 I1 + ( z22 + Z L ) I 2 = 0
(27)
Resolvendo (27) para I2 resulta que
z11 + Z g
z21
I2 =
z11 + Z g
Vg
0
z12
=−
11
z22 + Z L
z21
(z
z21 Vg
+ Z g ) ( z22 + Z L ) − z12 ⋅ z21
(28)
A tensão de Thevenin VTh vista da porta 2 é igual a V2 quando I2 é
nula, ou seja
VTh = V2 = ( z21I1 + z22 I 2 ) I
2 =0
= z21I1
(29)
Utilizando as expressões (18.a) e (18.c) com I2 nula vem que
⎧ V1 = z11I1
⎨
⎩ V1 = Vg − Z g I1
(30)
Rearranjando os termos vem que
⎧ V1 − z11I1 = 0
⎨
⎩ V1 + Z g I1 = Vg
(31)
Resolvendo para I1 vem que
1
I1 =
0
1 Vg
1 − z11
1 Zg
=
Vg
Z g + z11
(32)
8 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Substituindo (32) em (29) vem que
VTh =
z21
Vg
Z g + z11
(33)
A impedância de Thevenin ZTh vista da porta 2 é igual à relação
V2 / I2 quando Vg é nula. Para Vg = 0, a equação (18.c) fica na forma
V1 = − Z g I1
(34)
Substituindo (34) em (18.a) vem que
− Z g I1 = z11 I1 + z12 I 2
(35)
Rearranjando os termos vem que
z12
I2
Z g + z11
I1 = −
(36)
Substituindo (36) na equação (18.b) resulta que
V2 = − z21
⎛
z12
z12 ⎞
I 2 + z22 I 2 = ⎜ z22 − z21
⎟⎟ I 2
⎜
Z g + z11
Z
z
+
g
11 ⎠
⎝
(37)
Ou finalmente que
ZTh =
V2
I2
= z22 − z21
Vg = 0
z12
Z g + z11
(38)
O ganho de corrente I2 / I1 pode ser obtido diretamente a partir
da equação (22), ou seja
I2 = −
z21
I1
z22 + Z L
I2
z21
=−
I1
z22 + Z L
(39)
Para se calcular o ganho de tensão V2 / V1 é necessário substituir
o valor de I2 da equação (18.d) na equação (18.b), ou seja
⎛ V
V2 = z21 I1 + z22 ⎜ − 2
⎝ ZL
⎞
z22
V2
⎟ = z21 I1 −
ZL
⎠
9 de 19
(40)
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Em seguida determinar o valor de I1 na equação (18.a), também
utilizando (18.d), ou seja
⎛ V ⎞
z11 I1 = V1 − z12 I 2 = V1 − z12 ⎜ − 2 ⎟
⎝ ZL ⎠
(41)
Rearranjando os termos em (41) e resolvendo para I1 vem que
I1 =
z12 ⎞
1 ⎛
V
+
V2 ⎟
⎜ 1
z11 ⎝
ZL ⎠
(42)
Substituindo (42) em (40) vem que
⎡1 ⎛
⎞⎤ z
z
V2 = z21 ⎢ ⎜ V1 + 12 V2 ⎟ ⎥ − 22 V2
Z L ⎠⎦ Z L
⎣ z11 ⎝
(43)
A expressão (43) é função apenas de V1 e V2. Desta forma,
rearranjando os termos vem que
V2 +
z22
z z
z
V2 − 21 12 V2 = 21 V1
ZL
z11Z L
z11
(44)
Ou ainda que
⎛ z22 z21 z12 ⎞
z21
+
−
V
=
V1
1
⎜
⎟ 2
Z
z
Z
z
⎝
11 L ⎠
11
L
(45)
Ou
z21
z11
z21
V2
z11
=
=
=
z22 z21 z12
z11 Z L + z11 z22 − z21 z12
V1
−
1+
Z L z11 Z L
z11 Z L
(46)
Ou finalmente
V2
z21 Z L
z21 Z L
=
=
V1 z11 ( z22 + Z L ) − z21 z12 z11 Z L + ∆z
(47)
Fica a cargo do leitor provar que
V2
z21Z L
=
Vg ( z11 + Z g ) ( z22 + Z L ) − z21 z12
10 de 19
(48)
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Exemplo: Determinar as seis características básicas do circuito ao
lado considerando que este quadripolo está sendo alimentado por
uma fonte de tensão de 10 V com resistência interna de 2 Ω e está
alimentando uma carga de 3 Ω.
2Ω
I1
I2
10 Ω
+
V1
10 V
8Ω
9Ω
3Ω
−
V2
3Ω
Figura 5
Inicialmente é necessário o cálculo dos parâmetros z do quadripolo
em questão. Assim procedendo vem que:
z11 =
z21 =
z22 =
z12 =
= ( ( 3 // 9 ) + 10 ) // 8 = 4,840 Ω
V1
I1
I2 =0
V2
I1
( 3// 9 ) V
1
3// 9 ) + 10
(
( 3// 9 ) ⋅ V1 = 0,184 ⋅ 4,84 = 0,889 Ω
=
=
I1
( 3// 9 ) + 10 I1
I =0
V2
I2
V1
I2
(49)
(50)
2
= ( 3// 9 // (10 + 8 ) ) = 2,0 Ω
(51)
8
V2
V
8
+
8
10
=
=
⋅ 2 = 0, 444 ⋅ 2, 0 = 0,889 Ω
I2
8 + 10 I 2
(52)
I1 = 0
I1 =0
Os valores das seis características são então obtidos utilizando-se
as expressões determinadas anteriormente, ou seja:
Z in (1)
z12 z21
0,8892
= z11 −
= 4,84 −
= 4, 68 Ω
z22 + Z L
2, 0 + 3, 0
(53)
0,889 ⋅ 10
= 0, 266 A
( 4,84 + 2 )( 2 + 3) − 0,889 ⋅ 0,889
(54)
I2 = −
11 de 19
Circuitos de Duas Portas - Quadripolos
VTh =
® Clever Pereira / UFMG
z21
0,889
Vg =
⋅10 = 1,30 V
Z g + z11
2 + 4,84
(55)
z12
0,8892
ZTh = z22 − z21
= 2−
= 1,884 Ω
2 + 4,84
Z g + z11
(56)
I2
z21
0,889
=−
=−
= 0,178 Ω
2+3
I1
z22 + Z L
(57)
V2
z21 Z L
0,889 ⋅ 3
=
=
= 0,114
V1 z11 Z L + ∆z 4,84 ⋅ 3 + 8,89
(58)
V2
z21 Z L
0,889 ⋅ 3
=
=
= 0, 080
Vg ( z11 + Z g ) ( z22 + Z L ) − z21 z12 ( 4,84 + 2 )( 2 + 3) − 0,8892
(59)
6. CIRCUITOS DE DUAS PORTAS RECÍPROCOS
Um quadripolo é dito recíproco quando seus parâmetros satisfazem
as seguintes equações:
⎧
⎪
⎪
⎪⎪
⎨
⎪
⎪
⎪
⎪⎩
z12 = z21
y12 = y21
∆a = a11a22 − a12 a21 = 1
∆b = b11b22 − b12b21 = 1
(60)
h12 = − h21
g12 = − g 21
Nos quadripolos recíprocos, a troca de uma fonte ideal de tensão
em uma das portas por um amperímetro na outra porta resulta na
mesma leitura do amperímetro. Nestes circuitos são necessários
apenas três cálculos ou medidas para determinar um conjunto de
parâmetros.
12 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Um quadripolo recíproco é simétrico (ou bilateral) se seus
parâmetros satisfazem as seguintes equações adicionais:
⎧
⎪
⎪
⎪⎪
⎨
⎪
⎪
⎪
⎪⎩
z11 = z22
y11 = y22
a11 = a22
b11 = b22
(61)
∆h = h11h22 − h12 h21 = 1
∆g = g11 g 22 − g12 g 21 = 1
Neste tipo de circuito, a troca de uma porta pela outra não tem
nenhum efeito sobre as tensões e correntes e são necessários
apenas dois cálculos ou medidas para se determinar seus
parâmetros.
NOTA: Linhas de transmissão de energia elétrica são exemplos de
circuitos recíprocos e simétricos, também chamados de bilaterais.
7. CIRCUITOS DE DUAS PORTAS INTERLIGADOS - FORMAS
BÁSICAS
A figura 6 abaixo mostra as formas de se interligar quadripolos.
Cascata
Série
Paralela
Paralela-Série
Série-Paralela
Figura 6
13 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
6.1. Análise da ligação em cascata de dois quadripolos
Considere a ligação de dois quadripolos QA e QB em série, como
mostra a figura 7 abaixo
I1
I1A
I2 A
QA
V1A
I2
V2 A
V2
V1
I1A
I2 A
QB
V2 B
Figura 7
Utilizando os parâmetros de impedância Z, pode-se escrever para
os dois quadripolos que
⎡V1 A ⎤ ⎡ z11 A
⎢V ⎥ = ⎢ z
⎣ 2 A ⎦ ⎣ 21 A
z12 A ⎤ ⎡ I1 A ⎤
⋅
z22 A ⎥⎦ ⎢⎣ I 2 A ⎥⎦
⇒
iA ⋅IA
VA =Z
(62)
⎡V1B ⎤ ⎡ z11B
⎢V ⎥ = ⎢ z
⎣ 2 B ⎦ ⎣ 21B
z12 B ⎤ ⎡ I1B ⎤
⋅
z22 B ⎥⎦ ⎢⎣ I 2 B ⎥⎦
⇒
iB ⋅IB
VB = Z
(63)
Pela figura 7 o leitor pode verificar que
⎧ V1 = V1 A + V1B
⎨
⎩ V2 = V2 A + V2 B
⇒
V = V A +V B
(64)
⎧ I1 = I1 A = I1B
⎨
⎩ I2 = I2 A = I2B
⇒
I = IA = IB
(65)
14 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Assim, substituindo (62) e (63) em (64) vem que
iA ⋅IA + Z
iB ⋅IB
V =Z
(66)
Substituindo (65) em (66) vem que
(
)
iA ⋅I + Z
iB ⋅I = Z
iA + Z
iB ⋅I = Z
i⋅I
V =Z
(67)
A equação (67) mostra que a matriz Z do quadripolo equivalente é
a soma das matrizes Z dos quadripolos individuais ligados em
série.
6.2. Análise da ligação em cascata de dois quadripolos
Considere a ligação de dois quadripolos QA e QB em cascata, como
mostra a figura 8 abaixo
I1
V1
I1A
I2 A
QA
V1A
V2 A
V1B
I2
I 2B
I1B
QB
V2B
V2
Figura 8
Utilizando os parâmetros de transmissão, pode-se escrever para os
dois quadripolos que
⎡V1 A ⎤ ⎡ a11 A
⎢ I ⎥ = ⎢a
⎣ 1 A ⎦ ⎣ 21 A
a12 A ⎤ ⎡ V2 A ⎤
⋅
a22 A ⎥⎦ ⎢⎣ − I 2 A ⎥⎦
(68)
⎡V1B ⎤ ⎡ a11B
⎢ I ⎥ = ⎢a
⎣ 1B ⎦ ⎣ 21B
a12 B ⎤ ⎡ V2 B ⎤
⋅
a22 B ⎥⎦ ⎢⎣ − I 2 B ⎥⎦
(69)
onde
⎡a
i
A A = ⎢ 11 A
⎣ a21 A
a12 A ⎤
a22 A ⎥⎦
(70)
15 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
e
⎡a
i
AB = ⎢ 11B
⎣ a21B
a12 B ⎤
a22 B ⎥⎦
(71)
Substituindo (70) e (71) em (68) e (69) vem que
⎡V1 A ⎤ i ⎡ V2 A ⎤
⎢ I ⎥ = AA ⋅ ⎢− I ⎥
⎣ 1A ⎦
⎣ 2A ⎦
(72)
⎡V1B ⎤ i ⎡ V2 B ⎤
⎢ I ⎥ = AB ⋅ ⎢ − I ⎥
⎣ 1B ⎦
⎣ 2B ⎦
(73)
Pela figura 8 o leitor pode verificar que
⎡V1B ⎤ ⎡ V2 A ⎤
⎢ I ⎥ = ⎢− I ⎥
⎣ 1B ⎦ ⎣ 2 A ⎦
(74)
Substituindo (74) em (72) vem que
⎡V1 A ⎤ i ⎡V1B ⎤
⎢ I ⎥ = AA ⋅ ⎢ I ⎥
⎣ 1A ⎦
⎣ 1B ⎦
(75)
Substituindo (73) em (75) vem que
⎡V1 A ⎤ i ⎡V1B ⎤ i i ⎡ V2 B ⎤
⎢ I ⎥ = A A ⋅ ⎢ I ⎥ = A A ⋅ AB ⋅ ⎢ − I ⎥
⎣ 1A ⎦
⎣ 1B ⎦
⎣ 2B ⎦
(76)
Pela figura 8 o leitor pode verificar que
⎡V1 A ⎤ ⎡V1 ⎤
⎢I ⎥ = ⎢I ⎥
⎣ 1A ⎦ ⎣ 1 ⎦
(77)
⎡ V2 B ⎤ ⎡ V2 ⎤
⎢− I ⎥ = ⎢− I ⎥
⎣ 2B ⎦ ⎣ 2 ⎦
Substituindo (77) em (76) resulta que
⎡V1 ⎤ i i ⎡ V2 ⎤ i ⎡ V2 ⎤
⎢ I ⎥ = A A ⋅ AB ⋅ ⎢ − I ⎥ = A ⋅ ⎢ − I ⎥
⎣ 1⎦
⎣ 2⎦
⎣ 2⎦
16 de 19
(78)
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
A equação (78) mostra que a matriz de transmissão iAA do
quadripolo resultante da associação em cascata dos quadripolos
i BB dos
QA e QB é dada pela multiplicação das matrizes iAAAA e A
quadripolos originais.
Exemplo: Projetar um circuito LC terminado com um resistor de
1 Ω que possua a função de transferência de um filtro passa-baixa
de Butherworth dada por
H (s) =
1
s3 + 2s 2 + 2s + 1
(79)
De início é adequado agrupar o denominador em partes pares e
ímpares, ou seja
H (s) =
1
1
=
=
s 3 + 2 s 2 + 2 s + 1 ( s 3 + 2 s ) + ( 2 s 2 + 1)
1
s3 + 2s
=
=
3
2
2
2
1
+
+
+
s
s
s
(
) (
)
s3 + 2s
1
s3 + 2s
2s 2 + 1
1+ 3
s + 2s
(80)
Utilizando os parâmetros y de um quadripolo pode-se escrever que
⎧ I1 = y11V1 + y12V2
⎨
⎩ I 2 = y21V1 + y22V2
(81)
Com o quadripolo terminado por uma resistência YL tem-se também
que
I 2 = −YLV2
(82)
Substituindo (82) em (81.b) vem que
− YLV2 = y21V1 + y22V2
(83)
17 de 19
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Ou seja, a função de transferência do filtro vai ser dada por
H (s) =
V2 ( s )
y21
=−
V1 ( s )
YL + y22
y21
y21
YL
YL
=−
=−
YL + y22
y
1 + 22
YL
YL
(84)
Desta forma
⎧
⎪
⎪
⎨
⎪
⎪⎩
y21
1
= 3
YL s + 2 s
(85)
y22 2 s 2 + 1
=
YL s 3 + 2 s
Como YL = 1 S, então
1
⎧
=
y
21
3
⎪⎪
s + 2s
⎨
2
⎪ y = 2s + 1
22
s3 + 2s
⎩⎪
(86)
Como o filtro é de terceira ordem, será utilizado o circuito mostrado
na figura 9 abaixo
L1
V1(s)
L2
C
V2(s)
Fig. 9 – Filtro de Butherworth de 3ª ordem
Para este filtro o valor de y22 é da forma
y22 =
I2
V2
V1 = 0
⎛
⎛ s 2 L1C + 1 ⎞ 1
1 ⎞ 1
⎜ sC +
⎟⋅
⎜
⎟⋅
sL
sL
sL
sL2
1 ⎠
2
= ⎝
= ⎝ 2 1 ⎠
⎛
⎛ s L1C + 1 ⎞ 1
1 ⎞ 1
sC
+
+
⎜
⎟
⎜
⎟+
sL
sL
sL
⎝
⎝
⎠ sL2
1 ⎠
2
1
18 de 19
(87)
Circuitos de Duas Portas - Quadripolos
® Clever Pereira / UFMG
Desenvolvendo um pouco mais resulta em
y22 =
I2
V2
=
V1 = 0
s 2 L1C + 1
s 2 L1 L2
sL2 ( s L1C + 1) + sL1
2
=
s 2 L1 L2
(88)
s 2 L1C + 1
s 2 L1C + 1
=
= 3
s L1 L2 C + s ( L2 + L1 )
sL2 ( s 2 L1C + 1) + sL1
Comparando as equações (88) e (80) vem que
⎧ L1C = 2
⎪
⎨ L1 L2 C = 1
⎪L +L =2
1
⎩ 2
(89)
Resolvendo a equação (89) resulta finalmente que
L2 = 0,5 H
L1 = 1,5 H
C=
(90)
2
F = 1,33 F
1.5
Fica a cargo do leitor provar que a implementação de y22 irá
implementar y21 automaticamente, visto que, como y22 é a
admitância de curto-circuito vista da porta 2, ela já fornece uma
informação integral de todo circuito.
19 de 19