Método dos Elementos Finitos

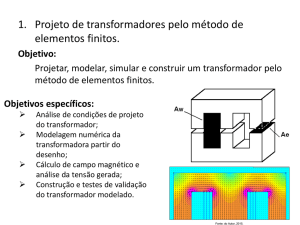
Teoria das Estruturas II
Método dos Elementos Finitos
Elementos Finitos
I. Estados Planos de Tensão e Deformação.
1. Estática e Cinemática de Peças Laminares
onde bi são as forças do corpo ou ligação (massa, pressão de fundação, etc.) e σ12 = σ21 uma
vez que as componentes das tensões tangenciais, que actuam em duas facetas ortogonais e
são perpendiculares à aresta comum às duas facetas, são iguais e têm sentidos tais que
convergem ambas para a aresta comum ou divergem ambas da mesma. É o que chamamos
de reciprocidade das tensões tangenciais.
Estas equações aplicam-se a estruturas laminares, delgadas e espessas.
CINEMÁTICA
Sabemos que a deformada final de um corpo pode ser representada como a acção
conjunta de deformações puras (extensões e distorções) e movimentos de corpo rígido
(translações e rotações). Assim,
1
Teoria das Estruturas II
Método dos Elementos Finitos
ESTÁTICA
 ∂
 ε11   ∂x1

 

 ε 22  =  0


2ε12   ∂
 ∂x 2

0 

∂   u1 
 
∂x 2  u 2 
∂ 

∂x1 
⇔
ε =∂u
NOTA : ε12 é a extensão de corte usada em cálculo tensorial
γ12 = 2ε12 é a extensão de corte usada em engenharia (também chamada de distorção)
2
Teoria das Estruturas II
 ∂
 ∂x
 1
 0

Método dos Elementos Finitos
∂   σ11 
∂x 2     b1  0
 σ +
=
∂   22  b  0
   2  
∂x1  σ12 
0
∂
∂x 2
⇔
∂Tσ + b = 0
2. Relações Constitutivas de Elasticidade para Peças Laminares
Como hipótese base, suponha-se que o material é isotrópico, isto é, tem as mesmas
características em todas as direcções e que temos elasticidade linear.
σ = Dε
ε = Cσ
;
onde D é a matriz de elasticidade (tensões internas relacionadas com extensões) e C é a
matriz de reciprocidade (extensões relacionadas com tensões internas).
( i ) Estados Planos de Tensão
Consideramos uma estrutura laminar e não vamos considerar tensões na direcção z.
σ 33 = σ 32 = σ 31 = 0
Podemos citar como exemplo placas finas que surgem em problemas de Engenharia
de Estruturas.
1

E 
D=
υ
1 - υ2 

 0
υ
1
0



0 
1

(1 − υ)
2

0
onde υ é o coeficiente de Poisson e E é o módulo de elasticidade.
3
Teoria das Estruturas II
Método dos Elementos Finitos
( ii ) Estados Planos de Deformação
Supõem-se que o material não pode alongar na direcção z.
ε 33 = ε 32 = ε 31 = 0
Também aqui, podemos citar como exemplo fundações, barragens, tensões em
túneis e condutas.
(1 − υ)

E

υ
D=
(1 - υ)(1 − 2υ) 

 0
υ
(1 − υ)
0



0

1

(1 − 2υ)
2

0
onde, mais uma vez, υ é o coeficiente de Poisson e E é o módulo de elasticidade.
Até agora convertemos deslocamentos em extensões (cinemática), extensões em
tensões (relações constitutivas) e as tensões em forças (estática).Há a necessidade de passar
do contínuo para uma discretização finita (aproximada), para o que se tem de definir o
modelo de aproximação a adoptar.
3. Modelos de Aproximação
O modelo mais simples é o correspondente à interpolação linear, no qual o
polinómio é definido por dois pontos.
Os valores da função f(x) para x compreendido entre x1 e x2 são aproximados para,
f(x) = φ1(x)f1 + φ2(x)f2
4
Teoria das Estruturas II
Método dos Elementos Finitos
FUNÇÕES BÁSICAS
ξ1 + ξ2 = 1
Neste caso, podemos introduzir um sistema de coordenadas homogéneas, ξ1 e ξ2.
Caso φ2(x) = 0,
Caso φ1(x) = 0,
Como vamos considerar uma única coordenada dentro do intervalo,
φ1(x) = ξ1
5
;
φ2(x) = ξ2
Teoria das Estruturas II
Método dos Elementos Finitos
Para o modelo linear o polinómio tem uma forma característica muito simples,
relacionando as coordenadas do sistema.
Num modelo de interpolação quadrático seriam necessários três pontos para definir
o polinómio. Caso fosse expresso em termos das coordenadas homogéneas, verificar-se-ia
que era quadrático em termos de ξi.
Vamos supor que a deformada de cada elemento pode ser representada por um
polinómio do 3º grau. Já sabemos que quando se consideram os efeitos das cargas axiais
esta deformada não é uma aproximação correcta.
Além disso, vamos ter necessidade de efectuar interpolações na função f(x) dado
que só a conhecemos em alguns pontos específicos e pretendemos prever qual o seu valor
noutros pontos.
No caso da aproximação por um polinómio de 2º grau, poder-se-ia passar uma
parábola por três pontos.
Quando não for possível calcular os integrais através das expressões analíticas
podem utilizar-se métodos numéricos como, por exemplo, a quadratura de Gauss, que exige
a integração numérica de pontos interiores.
6
Teoria das Estruturas II
Método dos Elementos Finitos
Se além dos valores das funções em dois pontos, também poderíamos determinar os
valores das derivadas nesses pontos, vamos ter quatro elementos para definir um modelo
cúbico.
Neste capítulo, o estudo de estruturas laminares sujeitas a estados planos será feito
de uma forma analógica à do comportamento das vigas à flexão :
•
O intervalo de variação da função corresponde a cada elemento ou
membro;
•
Os pontos vão significar os nós ou extremidades das barras da descrição
considerada.
4. Aplicação aos Elementos Planos
Numa placa em lugar de se considerar apenas um eixo, tal como no estudo de peças
lineares, vamos ter uma área. Considera-se que os deslocamentos do elemento se verificam
no próprio plano.
Neste caso em lugar de uma abcissa temos duas coordenadas que tem de ser
representadas no espaço.
7
Teoria das Estruturas II
Método dos Elementos Finitos
Se a figura geométrica a considerar for um triângulo ou um quadrilátero em que os
nós correspondem aos vértices, depois do carregamento os nós deslocam-se para uma nova
posição. No modelo de interpolação linear os lados mantém-se rectos e a matriz B é linear.
No modelo de deformação quadrático, tudo se vai passar do mesmo modo. Agora
vão ser acrescentados pontos correspondentes ao meio dos lados e a matriz B deixa de ser
linear.
4.1. Modelo Triangular para Deslocamentos Lineares
Consideram-se seis graus de liberdade correspondentes aos deslocamentos
horizontais e verticais dos vértices.
8
Teoria das Estruturas II
Método dos Elementos Finitos
Dado um ponto no plano interior, vamos determinar as funções coordenadas em
termos de φ1, φ2 e φ3 a partir dos valores de f1, f2 e f3.
f(x1, x2) = φ1(x1, x2)f1 + φ2(x1, x2)f2 + φ3(x1, x2)f3
Para obtermos a função básica φ1 vamos fazer f2 = f3 = 0.
A superfície gerada vai ser,
Dado uma origem e o sentido dos eixos coordenados, as funções básicas vão variar
em termos de x1 e x2, pelo que não nos interessa.
Se considerarmos um ponto interior e definirmos as áreas parciais em que se divide
o triângulo elementar, opostas ao nó correspondente, vamos obter um novo sistema de
coordenadas homogéneas.
Ai : área parcial
;
A : área total (do triângulo 123) ! A = ΣAi
9
;
ξi =
Ai
A
Teoria das Estruturas II
Método dos Elementos Finitos
Observações :
1) Quando o ponto interior P se desloca em direcção ao nó 1, A2 e A3 ! 0 e A1 ! A.
qualquer ponto do triângulo pode
P ≡ 1 ⇒ (ξ1,ξ2,ξ3) = (1,0,0) ⇒
ser representado em termos das
coordenadas
cartesianas
ou
homogéneas.
1 1 1
2) A posição do centro de gravidade G corresponde a  , , 
3 3 3
3) Este sistema de coordenadas básicas não varia com x1 e x2, dependendo apenas
da localização de P
f = α1ξ1 + α2ξ2 + α3ξ3
em que vamos determinar os valores de α1, α2 e α3 de acordo com os valores conhecidos de
f.
No interior do triângulo os deslocamentos horizontais e verticais são,
respectivamente,
u1 = φ1u11 + φ2u12 + φ3u13
u2 = φ1u21 + φ2u22 + φ3u23
Então, vamos ter
 ∂
 ε11   ∂x1

 

 ε 22  =  0


2ε12   ∂
 ∂x 2
10

0 

∂   x1 
 
∂x 2   x 2 
∂ 

∂x1 
Teoria das Estruturas II
Método dos Elementos Finitos
ε11 =
∂ u 1 ∂φ1
∂φ
∂φ
=
u 11 + 1 u 12 + 1 u 13
∂x1
∂x1
∂x1
∂x1
onde,
∂φ1 ∂φ1 ∂ξ1 ∂φ1 ∂ξ 2 ∂φ1 ∂ξ 3
=
⋅
+
⋅
+
⋅
∂x1 ∂ξ1 ∂x1 ∂ξ 2 ∂x1 ∂ξ 3 ∂x1
Mas,
φ1 = x1
e
ε11 = u11 ⇒ as extensões são constantes dentro do triângulo elementar.
1  1
  
 x1  =  x11
  
 x 2   x 21
1
x12
x 22
1   ξ1 
  
x13  ξ 2 
 
x 23  ξ 3 
Da expressão anterior,
 ξ1 
2A 23
 
1 
 2A 31
ξ 2  =
  2A 
 2A12
ξ 3 
b1
b2
b3
a1   1 
  
a 2   x1 
 
a 3   x 2 
onde,
2A23 = 2×área(023) = x12x23 − x13x22 ; a1 = x13 − x12 ; b1 = x22 − x23
2A31 = 2×área(031) = x13x21 − x11x23 ; a2 = x11 − x13 ; b2 = x23 − x21
2A12 = 2×área(012) = x11x22 − x12x21 ; a3 = x12 − x11 ; b3 = x21 − x22
11
Teoria das Estruturas II
Método dos Elementos Finitos
Um modelo de deslocamentos linear pode ser dado directamente em termos de ξ1, ξ2
e ξ3,
 u 1  φ
u= =
u 2  0
0 u 1e  φ1
  = 
φ u e2   0
φ2
φ3
0
0
0
0
φ1
φ2
 u 11 
 
 u 12 
 
0   u 13 
   = Nu e
φ 3  u 21 
 
u 22 
 
u 23 
O modelo de interpolação linear conduz a
φ = [ξ1
ξ2
ξ3 ]
Atendendo ao sistema de equações que relaciona as coordenadas cartesianas e as
homogéneas e diferenciando φi em ordem a x1 e x2, respectivamente, vamos ter
∂φ
∂φ 
∂φ i ∂φ i ∂ξ1 ∂φ i ∂ξ 2 ∂φ i ∂ξ 3
1  ∂φ i
1
=
×
+
×
+
×
=
+ b2 i + b3 i  =
bi
b1
∂x1 ∂ξ1 ∂x1 ∂ξ 2 ∂x1 ∂ξ 3 ∂x1 2A  ∂ξ1
∂ξ 2
∂ξ 3  2A
∂φ i ∂φ i ∂ξ1 ∂φ i ∂ξ 2 ∂φ i ∂ξ 3
∂φ
∂φ 
1  ∂φ i
1
ai
=
×
+
×
+
×
=
+ a 2 i + a3 i  =
a1
∂ξ 2
∂ξ 3  2A
∂x 2 ∂ξ1 ∂x 2 ∂ξ 2 ∂x 2 ∂ξ 3 ∂x 2 2A  ∂ξ1
4.2. Relações de Compatibilidade
O vector das extensões é dado por,
ε = Bue
12
Teoria das Estruturas II
 ∂
ε
 11   ∂x1

 

 ε 22  =  0


2ε12   ∂
 ∂x 2
b1
1 
0
=
2A 
 a1
Método dos Elementos Finitos

0 

∂  φ1

∂x 2   0
∂ 

∂x1 
φ2
φ3
0
0
0
0
φ1
φ2
b2
b3
0
0
0
0
a1
a2
a2
a3
b1
b2
 u 11 
 
 u 12 
 
0   u 13 
  =
φ 3  u 21 
 
u 22 
 
u 23 
 u 11 
 
 u 12 
0  
  u 13 
a3   
  u 21 
b 3   
u 22 
 
u 23 
Rearranjando este sistema de equações para escrever as equações de cada nó
 ε11 
b1

 1 
0
 ε 22  =
2A



 a1
2ε12 
0
b2
0
b3
a1
0
a2
0
a2
a3
b1
b2
4.3. Relações de Equilíbrio de Elementos
A Energia de Deformação Total é dada por,
U=
1
(ε − ε 0 )T D (ε − ε 0 ) dV
∫
2
13
 u 11 
 
 u 12 
0  
  u 13 
a3   
 u 21 
b 3   
u 22 
 
u 23 
Teoria das Estruturas II
Método dos Elementos Finitos
onde dV é o volume de cada elemento infinitesimal
A Energia de Deformação é, portanto, dada pela área limitada superiormente pela
linha indicada. Como em cada elemento triangular, vamos ter 3 extensões e 3 tensões.
A Energia Total Potencial é dada por,
V=U−W
onde W é o trabalho realizado pelas forças de ligação, forças de superfícies e as forças
nodais (cada elemento finito está ligado aos outros por intermédio de nós, sendo apenas
estes que transmitem as forças nodais, Fe). O trabalho realizado é dado pela soma dos
termos do tipo u1ε1, u2ε2.
V=
T
1 T
1
T
T
ε D ε dV − ∫ ε 0 D ε dV + ∫ ε 0 D ε 0 dV − ∫ b T u dV − ∫ p T u ds − F e u e
∫
2
2
Introduzindo o modelo de elementos finitos,
u = N ue ; ε = B ue
V=
T
1 eT
1
T
ε 0 D ε 0 dV − b T N dV u e − p T N ds u e − F e u e
u
B T D B dV u e − ε 0 D B dV u e +
2
2
∫
∫
∫
∫
14
∫
Teoria das Estruturas II
Método dos Elementos Finitos
Deste modo, V torna-se uma função algébrica dos deslocamentos nodais ue, dado
que todos os integrais representam valores constantes. Das relações de equilíbrio de cada
elemento, temos que V tem de ser estacionária em relação a ue (equivale à aplicação da
Dualidade Estático-Cinemática), isto é :
∂V
= B T D B dV u e − ∫ B T D ε 0 dV − ∫ N T b dV − ∫ N T p ds − F e = 0
∂u e ∫
⇓
F e = ∫ B T D B dV u e − ∫ B T D ε 0 dV − ∫ N T b dV − ∫ N T p ds
No caso de considerarmos os efeitos dinâmicos para o cálculo de elementos finitos,
podemos representar as equações de movimento relativas aos nós da estrutura, a partir da
Energia Cinética Total, J.
J=
1
ρ u T u dV
∫
2
onde ρ é a densidade do material.
Supondo que no modelo elementar de velocidades a matriz N é independente do
tempo t, temos,
J=
1 eT
u ∫ ρ N T N dV u e
2
Usando as equações de Lagrange,
∂  ∂J  ∂J
∂V
 e − e + e =0
∂ t  ∂u  ∂u
∂u
o que dá,
F e = ∫ N T N dV u e + ∫ B T D B dV u e − ∫ B T D ε 0 dV − ∫ N T b dV − ∫ N T p ds
15
Teoria das Estruturas II
Método dos Elementos Finitos
Comentários :
1.
Estamos a utilizar técnicas de elementos finitos, discretizando a estrutura
laminar em triângulos elementares aos quais estamos a determinar as propriedades;
2.
É possível ter modelos elementares baseados em esforços internos e não em
deslocamentos nodais;
3.
O deslocamento final da estrutura é igual a soma das contribuições dos
elementos triangulares.
Vamos substituir o problema no contínuo, inicialmente dado por equações
diferenciais parciais, por um conjunto de equações lineares;
4.
No caso do Método das Diferenças Finitas vão-se integrar as equações
diferenciais numa grelha regular por um método numérico aproximado;
Podemos escrever,
dV = t × dA, sendo t a espessura da laje e
ds = t × dl
A matriz de rigidez será,
K e = ∫ B T D B dA × t = B T D B A × t
4.4. Vector das Cargas Aplicadas
Vector das cargas aplicadas (consistente com a formulação em elementos finitos) :
( i ) Extensões iniciais : Fεe0 = ∫ B T D ε 0 dA t = B T D ε 0 A t
( ii ) Forças de ligação : Fbe = ∫ N T b dA t = ∫ N T dA b t
sendo ε0 e b valores constantes. Para efectuar a integração utilizando a discretização
anteriormente indicada,
16
Teoria das Estruturas II
Método dos Elementos Finitos
φ T
F = ∫
 0
e
b
 φ T dA b1 
0   b1 
∫

 dA   t = 
t
T
φ T  b 2 
∫ φ dA b 2 
Como,
 ξ1 
 
T
d
φ
A
=
∫
∫ ξ 2  dA
 
ξ 3 
e a fórmula a que corresponde o integral de ∫ ξ1 ξ 2 ξ 3 dA será,
p
q
r
p! q! r!
× 2A
( p + q + r + 1)!
Exemplo : ∫ ξ1 dA =
1
A (dado que 0! = 1)
3
 b1 
 
 b1 
 
 b1 
1
1
Assim, Fbe = A t   , ou seja,
da força de ligação total vai para cada
3
3
b
 2
 
b 2 
 
b 2 
nó.
17
Teoria das Estruturas II
Método dos Elementos Finitos
4.5. Modelo de Deformação Quadrático
O modelo de deformações quadrático (considerando pontos intermédios) vai dar,
a)
Para um elemento linear (barra) :
 ξ1 2 − ξ1ξ 2 


 2

T
φ = ξ 2 − ξ1ξ 2  onde ξ1 = 1 − ξ 2


 4ξ1 ξ 2 
b)
Para um modelo triangular :
 ξ1 (2ξ1 − 1) 


ξ 2 (2ξ 2 − 1)


ξ 3 (2ξ 3 − 1) 


φT = 

 4ξ1ξ 2 


 4ξ 2 ξ 3 


 4ξ 3 ξ1 
18
Teoria das Estruturas II
Método dos Elementos Finitos
( iii ) Forças de superfície : Fpe = ∫ N T p dl t = ∫ N T dl p t
onde p é um valor constante.
Estas podem ser distribuídas ao longo da superfície, podendo variar quer a sua
intensidade, quer o ângulo de aplicação. Exprimem-se em unidade de força por unidade de
área e são geralmente de tracção. A força total é pois dada pela intensidade de força vezes a
área a que corresponde.
 φ T dl p1 
∫

F =
t
T
∫ φ dl p 2 
e
p
Como a fórmula a que corresponde o integral de ∫ ξ1 ξ 2 dl será,
p
q
p! q!
× l12
( p + q + 1)!
Exemplo : ∫ ξ1 dl =
1
l12
2
 p1 
 
 p1 
 
 0 
1
1
e
Assim, Fp = l12 t   , ou seja,
da força aplicada à superfície vai para
2
2
p 2 
 
p 2 
 
 0 
cada nó.
19
Teoria das Estruturas II
Método dos Elementos Finitos
4.6. Matriz de Massa (análise dinâmica)
No caso de existirem efeitos dinâmicos, temos de introduzir os termos relativos ao
desenvolvimento da Energia Cinética,
∫B
T
D B dV u e + ∫ ρN T N dV u e = Forças nodais dos diferentes tipos
onde ρ é a densidade do elemento triangular.
Obtemos assim um problema constituído por um conjunto de equações
diferenciais, definidas para os elementos em que se vão discretizar a estrutura.
As forças de massa correspondem ao termo
∫ρ N
T
N dV u e e são proporcionais à
aceleração dos deslocamentos nodais. A aceleração define-se como a segunda derivada em
ordem ao tempo dos deslocamentos nodais.
A matriz da massa será,
M e = ∫ ρN T N dA t = ρ ∫ N T N dA t
φ T
M = ρ t∫ 
 0
e
0  φ

φ T  0
0
φ T φ
 dA = ρ t ∫ 
 0
φ
Mas,
 ξ1 ξ1

T
d
A
φ
φ
=
∫
∫ ξ 2 ξ1
ξ 3 ξ1
ξ1ξ 2
ξ2ξ2
ξ3ξ 2
20
ξ1 ξ 3 

ξ 2 ξ 3  dA

ξ 3 ξ 3 
0 
 dA
φ T φ
Teoria das Estruturas II
Método dos Elementos Finitos
Da fórmula geral,
∫ξ
2
1
dA = ∫ ξ 2 dA = ∫ ξ 3 dA =
2
2
1
A
6
1
∫ ξ ξ dA = ∫ ξ ξ dA = ∫ ξ ξ dA = 12 A
1
2
1 3
2

1

ρ A t 1
e

M =
12 





2
1
1
2
1
1
2
3
2
1
1
2
1
1






1

1

2
As Forças de Restituição associadas à rigidez da estrutura tem um comportamento
semelhante a uma mola : a força exercida na mola aumenta proporcionalmente ao
deslocamento produzido.
Observações :
1.
Para as forças de ligação, considerou-se que se for adoptado este raciocínio
para a determinação da matriz de massa obtinham-se que
1
3
das cargas aplicadas no
elemento triangular está aplicada em cada nó). Neste caso, vamos obter soluções
mais inexactas, embora a matriz obtida seja diagonal ⇒ utilização de técnicas
numéricas mais simples
1
LA 

ρ
3 

1
21


 = me

1
Teoria das Estruturas II
2.
Método dos Elementos Finitos
No caso de termos cargas horizontais e a parede estar simplesmente apoiada
na fundação, considera-se a estrutura libertada ser do tipo porticado e rotulado na
base.
5. Exemplos
5.1. Aplicação a um problema de Estados Planos de Tensão
Considere a parede representada na figura sujeita ao carregamento indicado e ligada
ao solo.
Como os graus de liberdade são deslocamentos horizontais e verticais (não se
consideram rotações) considera-se a estrutura sendo a base contituída por apoios duplos.
Como a estrutura é simétrica, o comportamento dos dois lados do eixo de simetria é
idêntico, pelo que podemos suprimir os deslocamentos verticais e horizontais ao longo
deste eixo.
A estrutura está sujeita à um Estado Plano de Tensão.
22
Teoria das Estruturas II
Método dos Elementos Finitos
Discretizando a estrutura vem,
32 elementos
36 graus de liberdade
Para resolver o problema vamos produzir uma deformação no sistema devido a ui =
1 e vamos determinar quais os esforços que mantém o sistema numa posição deslocada.
Assim a Matriz de Rigidez vem,
5

0

− 4
Et 
Ke =
= − 2
6 
0

0


0
−4
−2
0
5
−1
−1
0
−1
10
3
−4
−1
3
10
−1
0
−4
−1
10
0
−2
−1
3
...



0


−2
... 

−1


3


10


(36×36 )
0
Notas :
1.
Cada ponto interior pode fazer a ligação de 6 triângulos;
2.
Se utilizarmos um sistema de coordenadas locais, ele deve ser transformado
num sistema de coordenadas globais.
23
Teoria das Estruturas II
Método dos Elementos Finitos
Cargas aplicadas :
 0   0 
1
γA t   = 

3
- 1 − 0.575
•
Peso próprio, Fbe =
•
Carregamento, Fpe = ∫ N T p dA
Caso a distribuição de cargas seja muito complicada, pode-se aproximar colocando
parte da carga aplicada em cada nó (por exemplo, no caso da carga distribuída vamos
mandar metade para cada lado).
Resolução do sistema Ku = F
A maior vantagem em utilizar a inversa de K é a de podermos determinar
imediatamente os deslocamentos correspondentes às diversas condições de carregamento.
u = K-1F
NOTA : Vamos considerar que no caso de haver um bom contacto entre a fundação e a parede, se desenvolve um efeito de arco.
Depois de se obterem os deslocamentos nodais, é possível obter os 6 deslocamentos
ue.
Com estes valores podemos determinar as extensões, ε, através da equação,
ε = Bue
As tensões no interior da peça são obtidas à custa da matriz de elasticidade D,
σ = Dε
24
Teoria das Estruturas II
Método dos Elementos Finitos
Observações :
1.
No caso do comportamento do material ser elásto-plástico, a equação que
nos dá as tensões é modificada, uma vez que a matriz das relações constitutivas
deixa de ser constante.
dσ = D(ε)dε
Neste tipo de comportamento temos necessidade de calcular a tangente em
cada ponto da curva de tensões-extensões ou de momentos-curvaturas.
2.
No caso de acrescentarmos pontos intermédios (nós intermédios) para o
cálculo de um modelo de deformações quadrático, cada elemento triangular estaria
associado a 12 graus de liberdade;
3.
O modelo definido aplica-se aos casos de cargas axiais que actuam no plano
médio da placa e que provoquem igualmente deslocamentos segundo o plano
intermédio da placa
No caso de haver cargas perpendiculares ao plano médio da laje, o modelo
que estudamos não é correcto porque entra com o movimento perpendicular ao
plano médio da placa, não satisfazendo a condição de compatibilidade da estrutura.
Para isso deve desenvolver-se um elemento para flexão em placas. Em seguida
apresenta-se um modelo deste tipo com 15 graus de liberdade.
25