I UNIDADE

RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA
2o ANO DO ENSINO MÉDIO
DATA: 08/03/14
PROFESSOR: MALTEZ
QUESTÃO 01
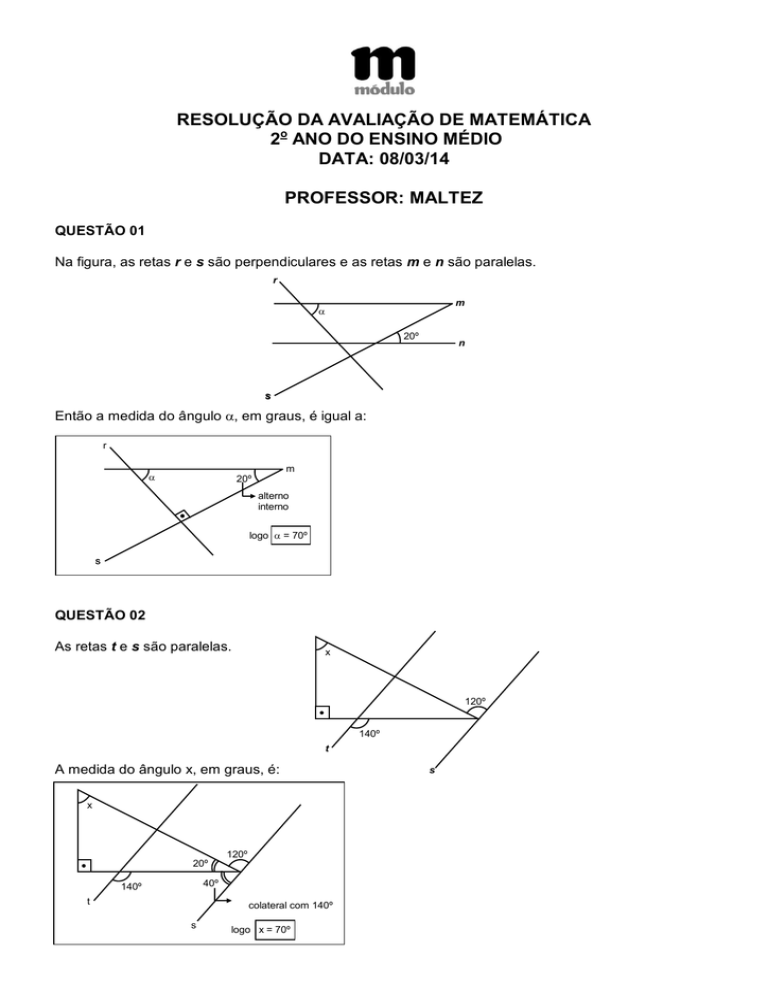
Na figura, as retas r e s são perpendiculares e as retas m e n são paralelas.
r
m

20º
n
s
Então a medida do ângulo , em graus, é igual a:
r
m

20º
alterno
interno
logo  = 70º
s
QUESTÃO 02
As retas t e s são paralelas.
x
120º
140º
t
A medida do ângulo x, em graus, é:
x
120º
20º
40º
140º
t
colateral com 140º
s
logo x = 70º
s
QUESTÃO 03
F
105º
Observe a figura ao lado. Nela os pontos F, A e B estão em uma reta e
as retas CB e ED são paralelas. Assim sendo, o ângulo AB̂C mede:
A
A
Seja E, D e G colineares:
75º
57º
E
D
Como
57º + 75º = 132º então o ângulo
57º
D
E
48º
AĜE  48º e como EG//BC o ângulo
G
C
B
AB̂C  48º (são correspondentes).
B
C
QUESTÃO 04
Ana e Maria estão se divertindo em uma roda-gigante, que gira em sentido
anti-horário e possui oito lugares equidistantes. Inicialmente, a roda encontra-se na posição indicada na figura, estando Maria na parte inferior e Ana
à meia altura entre as partes inferior e superior da roda.
A partir dessas informações, analise as proposições a seguir.
I)
II)
A roda deve girar 90° para que Ana alcance o topo.
Maria estará diretamente acima de Ana, na vertical, após a roda ter
girado 225° a partir do momento inicial.
III) Se a distância entre os pontos de sustentação das cadeiras de Ana e
Maria for igual a 4 2 m, então a circunferência que contém esses pontos e tem centro coincidente
com a da roda-gigante possui diâmetro maior que 9 m.
São verdadeiras:
I)
Verdadeiro, pois ao girar 90º, Ana completa um quadrante e ocupa o ponto superior.
II)
Após a roda-gigante girar 225º o posicionamento é o seguinte:
Maria
Portanto é Verdadeira.
Ana
III) Falso, pois
4 2 
r
r
2
 r2  r2
2r2 = 32
4 2
r2 = 16  r = 4
Logo 2r = 8 m
QUESTÃO 05
José deseja construir, com tijolos, um muro de jardim com a forma de
uma espiral de dois centros, como mostra a figura abaixo.
Para construir essa espiral, escolheu dois pontos que distam 1 metro um
do outro. A espiral tem 4 meias-voltas e cada tijolo mede 30 cm de comprimento.
Considerando  = 3, o número de tijolos necessários para fazer a espiral
é:
1a:
2 . 1
 3 . 1 3
2
3a:
2 . 3
3.39
2
2a:
2 . 2
2.36
2
4a:
2 . 4
 3 . 4  12
2
30m = 3000 cm
3000 : 30 = 100 tijolos
QUESTÃO 06
Na figura, A, B, C e D são pontos de uma circunferência, a corda CD é bissetriz do ângulo AĈB e as cordas AB e AC têm o mesmo comprimento. Se o
ângulo BÂD mede 40°, a medida  do ângulo BÂC é:
x = 40º  B̂  Ĉ  80º
logo  = 20º
x
80º
x
=
3000
QUESTÃO 07
A, B, C e D são vértices consecutivos de um hexágono regular. A medida de um dos ângulos formados
pelas diagonais AC e BD é:
E
D
C
B
BCD é isósceles
30º
F
C
ABC é isósceles
30º
A
D
A
B
Os ângulos são 60º e 120º. Como foi pedido um
dos ângulos, então a resposta é 120º.
QUESTÃO 08
Sejam as figuras:
D
I)
A
II)
D
x
III)
A
110º
x
B
C
A
x
B
C
82º
150º
B
D
C
Em todo quadrilátero inscrito, os ângulos opostos são suplementares, logo
I) x = 70º
II) x = 150º
III) x = 98º
QUESTÃO 09
Deseja-se instalar uma fábrica num lugar que seja equidistante dos municípios A, B e C. Admita que A,
B e C são pontos não colineares de uma região plana e que o triângulo ABC é escaleno.
Nessas condições, o ponto onde a fábrica deverá ser instalada é o:
A resposta é o circuncentro que significa o centro da circunferência que passa por A, B e C.
QUESTÃO 10
Para uma atividade realizada no laboratório de Matemática, um aluno precisa construir uma maquete da
quadra de esportes da escola que tem 28 m de comprimento por 12 m de largura. A maquete deverá
ser construída na escala de 1 : 250.
Que medidas de comprimento e largura, em cm, o aluno utilizará na construção da maquete?
1  x  x  11,2 cm
250 2800
1  y  y  4,8
250 1200
QUESTÃO 11
Um pátio de grandes dimensões vai ser revestido por pastilhas
quadradas brancas e pretas, segundo o padrão representado ao
lado, que vai ser repetido em toda a extensão do pátio.
As pastilhas de cor branca custam R$ 8,00 por metro quadrado e
as de cor preta, R$ 10,00. O custo por metro quadrado do revestimento será de:
Quantidade total de quadradinhos = 20 x 10 = 200
160 brancos  160 x 8 = 1280
40 pretos  40 x 10  400
1680 : 200 = 8,40
1280 +
400
1680
QUESTÃO 12
ABCDEFGH é um polígono regular convexo. Sabendo que PE é tangente ao círculo, qual a medida em
graus, do ângulo α?
Cada arco vale 45º (360º : 8)
  AE  CE  180  90  90º  45º
2
2
2
QUESTÕES DISCURSIVAS
QUESTÃO 01 (0,4)
O triplo do complemento de um ângulo, aumentado em 50º, é igual ao suplemento do ângulo. Determine a medida do ângulo.
3(90º – X) + 50º = 180º – x
270º – 3x + 50º = 180º – x
320º – 3x = 180º – x
320 – 180º = 3x – x
140º = 2x  x = 70º
QUESTÃO 02 (0,4)
r
3x – 10º
As retas r e s da figura ao lado são paralelas.
Determine x e y.
y + 90º + 2x = 180º
3x – 10º = y
y + 2x = 90º
3x – y = 10
y
2x
s
Somando membro a membro
5x = 100º  x = 20º
Como y + 2x = 90º  y + 40º = 90º
 y = 50º
QUESTÃO 03 (0,4)
Na figura abaixo, calcule o ângulo x, sendo  o triplo de  e  o sêxtuplo de .
A
 = x + 100º  6 = x + 100º

Como  +  = 100º e
E
3 +  = 100º
x

4 = 100º

80º
B
C
D
 = 25º
6 . 25 = x + 100º
150º = x + 100º
x = 50º
QUESTÃO 04 (0,4)
Calcule x e y na figura, se x = AB e y = CD.
B
D
xy
 80 º
2
xy
 25 º
2
x  y  160 º
x  y  50 º
 x  105 º
2x  210 º
então y = 55º
x
80º y
C
A
25º